Оглавление:
Наибольшее и наименьшее значения функции на отрезке
Пусть функция 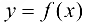 непрерывна на отрезке
непрерывна на отрезке 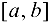 . Тогда на этом отрезке функция достигает наибольшего и наименьшего значений, теорема 4.3 Вейерштрасса (раздел 1). Будем предполагать, что на данном отрезке функция
. Тогда на этом отрезке функция достигает наибольшего и наименьшего значений, теорема 4.3 Вейерштрасса (раздел 1). Будем предполагать, что на данном отрезке функция 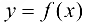 имеет конечное число критических точек. Если наибольшее и наименьшее значения достигаются внутри отрезка
имеет конечное число критических точек. Если наибольшее и наименьшее значения достигаются внутри отрезка 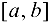 , то очевидно, что эти значения будут наибольшим максимумом и наименьшим минимумом функции (если имеется несколько экстремумов). Однако может наблюдаться такая ситуация, что наибольшее или наименьшее значения будут достигаться на одном из концов отрезка (рис. 9.1).
, то очевидно, что эти значения будут наибольшим максимумом и наименьшим минимумом функции (если имеется несколько экстремумов). Однако может наблюдаться такая ситуация, что наибольшее или наименьшее значения будут достигаться на одном из концов отрезка (рис. 9.1).
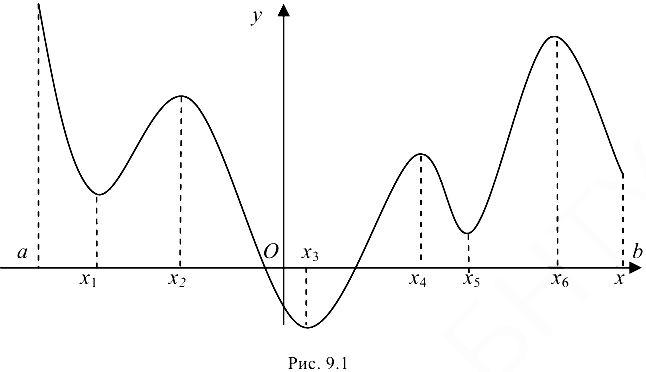
Таким образом, неприрывная функция 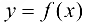 на отрезке достигает своего наибольшего и наименьшего значений либо на концах этого отрезка, либо в таких точках этого отрезка, которые являются точками экстремума.
на отрезке достигает своего наибольшего и наименьшего значений либо на концах этого отрезка, либо в таких точках этого отрезка, которые являются точками экстремума.
Исходя из вышесказанного, можно предложить следующий алгоритм поиска наибольшего и наименьшего значений непрерывной функции 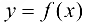 па отрезке
па отрезке 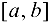 :
:
- Найти все критические точки. Если критическая точка
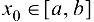 , то нужно вычислить в ней значение функции
, то нужно вычислить в ней значение функции 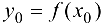 . Если критическая точка
. Если критическая точка 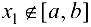 , то в дальнейшем решении эта точка во внимание не принимается.
, то в дальнейшем решении эта точка во внимание не принимается. - Вычислить значения функции на концах отрезка, т. е. найти
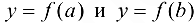 .
. - Из всех полученных выше значений функции выбрать наибольшее и наименьшее, они и будут представлять собой наибольшее и наименьшее значения функции
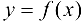 на отрезке
на отрезке 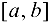 .
.
Пример 9.3.
Найти наибольшее и наименьшее значения функции 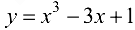 на отрезке [-3; 3].
на отрезке [-3; 3].
Решение:
Так как функция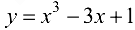 непрерывна на отрезке [-3; 3], то задача имеет решение.
непрерывна на отрезке [-3; 3], то задача имеет решение.
1. Найдем критические точки функции.
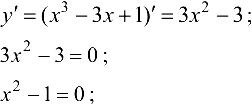
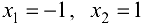 — критические точки.
— критические точки.
Так как 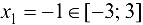 , то вычислим
, то вычислим 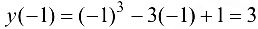 , так как
, так как 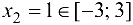 , то вычислим
, то вычислим 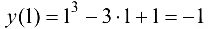 .
.
2. Определим значения функции на концах отрезка:
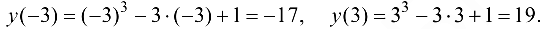
3. Сравним вычисленные значения функции и выберем наибольшее и наименьшее:
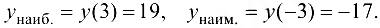
Ответ: 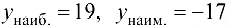 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

