Оглавление:
Рассмотрим линейное однородное уравнение второго порядка с постоянными коэффициентами, т.е. уравнение 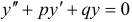 , где
, где 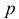 и
и 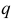 — постоянные числа.
— постоянные числа.
Чтобы найти общее решение этого уравнения, достаточно найти два линейно независимых частных решения в виде 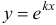 , где
, где 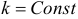 .
.
Подставляя эту функцию и ее производные 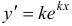 и
и 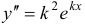 в рассматриваемое уравнение, получим:
в рассматриваемое уравнение, получим: 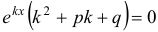 . Так как
. Так как 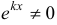 , значит
, значит 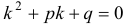 .
.
Следовательно, если 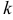 будет удовлетворять полученному уравнению, которое называется характеристическим, то
будет удовлетворять полученному уравнению, которое называется характеристическим, то 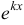 будет решением исходного уравнения.
будет решением исходного уравнения.
Характеристическое уравнение есть квадратное уравнение, имеющее два корня: обозначим их через 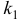 и
и 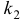 . При этом
. При этом
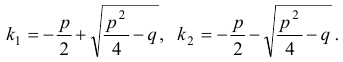
Здесь возможны следующие случаи:
а) Корни характеристического уравнения действительны и различны.
В этом случае частными решениями будут функции 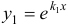 и
и 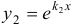 . Общим решением уравнения будет
. Общим решением уравнения будет 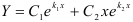 .
.
Пример №1
Решить уравнение 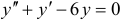 .
.
Решение:
Характеристическое уравнение имеет вид 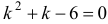 . Корни характеристического уравнения:
. Корни характеристического уравнения: 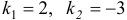 . Общее решение:
. Общее решение: 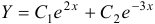 .
.
б) Корни характеристического уравнения действительные и равные.
В этом случае мы имеем только одно частное решение 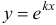 , т.к.
, т.к. 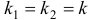 . При этом общее решение будет
. При этом общее решение будет 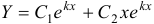 .
.
Пример №2
Решить уравнение  .
.
Решение:
Составим характеристическое уравнение 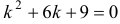 . Найдем его корни:
. Найдем его корни: 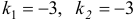 . Общим решением будет функция
. Общим решением будет функция 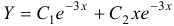 .
.
в) Корни характеристического уравнения комплексные.
Так как коэффициенты 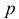 и
и 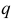 характеристического уравнения действительные числа, то комплексные корни будут сопряженными. Причем,
характеристического уравнения действительные числа, то комплексные корни будут сопряженными. Причем, 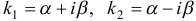 , где
, где 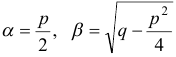 . Общее решение в рассматриваемом случае имеет вид
. Общее решение в рассматриваемом случае имеет вид 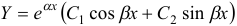 .
.
Пример №3
Найти частное решение уравнения 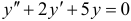 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 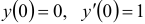 .
.
Решение:
Составим характеристическое уравнение 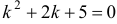 . Найдем его корни
. Найдем его корни 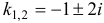 . Следовательно, общее решение есть
. Следовательно, общее решение есть 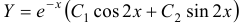 . Найдем теперь частное решение, удовлетворяющее заданным начальным условиям. На основании первого условия находим
. Найдем теперь частное решение, удовлетворяющее заданным начальным условиям. На основании первого условия находим 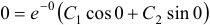 , откуда
, откуда 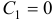 . Заметив, что
. Заметив, что 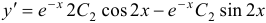 , из второго условия получаем:
, из второго условия получаем: 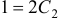 , т.е.
, т.е. 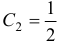 . Таким образом, искомое частное решение есть
. Таким образом, искомое частное решение есть 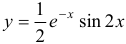 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Уравнения не содержащие: (y) |
| Уравнения, не содержащие x |
| Линейные неоднородные уравнения с постоянными коэффициентами |
| Метод вариации произвольных постоянных |

