Оглавление:
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами имеют вид 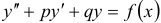 , где
, где 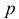 и
и 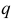 — действительные числа.
— действительные числа.
Общее решение линейного неоднородного уравнения представляется как сумма какого-нибудь частного решения 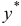 этого уравнения и общего решения
этого уравнения и общего решения 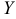 соответствующего однородного уравнения, т.е.
соответствующего однородного уравнения, т.е.  .
.
Вид частного у решения неоднородного уравнения зависит от вида правой части этого уравнения. Рассмотрим некоторые случаи.
а) 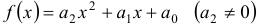 . Если
. Если 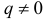 , то частное решение неоднородного уравнения ищем также в форме квадратного трехчлена:
, то частное решение неоднородного уравнения ищем также в форме квадратного трехчлена: 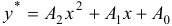 , где
, где 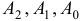 — неопределенные коэффициенты. Если
— неопределенные коэффициенты. Если 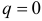 , то частное решение
, то частное решение 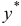 ищем в виде
ищем в виде 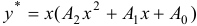 , когда один из корней характеристического уравнения равен нулю, и в виде
, когда один из корней характеристического уравнения равен нулю, и в виде 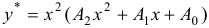 , когда оба корня характеристического уравнения нули. Аналогично обстоит дело, если
, когда оба корня характеристического уравнения нули. Аналогично обстоит дело, если 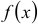 — многочлен
— многочлен 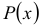 произвольной степени.
произвольной степени.
Пример №1
Решить уравнение 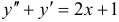 .
.
Решение:
Имеем: 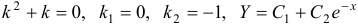 . Так как ноль — однократный корень характеристического уравнения, то частное решение данного уравнения ищем в виде
. Так как ноль — однократный корень характеристического уравнения, то частное решение данного уравнения ищем в виде 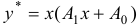 . Отсюда имеем:
. Отсюда имеем: 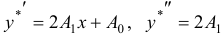 . Подставляем в исходное уравнение:
. Подставляем в исходное уравнение: 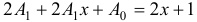 . Искомые коэффициенты будут:
. Искомые коэффициенты будут: 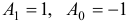 . Значит, частное решение будет
. Значит, частное решение будет 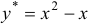 , а общее решение получается в виде
, а общее решение получается в виде 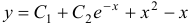 .
.
б) 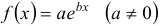 . Частное решение ищем в виде
. Частное решение ищем в виде 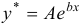 , где
, где 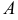 — неопределенный коэффициент. Если
— неопределенный коэффициент. Если 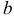 — корень характеристического уравнения, то частное решение ищем в виде
— корень характеристического уравнения, то частное решение ищем в виде 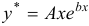 , когда
, когда 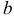 -однократный корень, и в виде
-однократный корень, и в виде 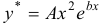 , когда
, когда 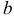 — двукратный корень. Аналогично будет, если
— двукратный корень. Аналогично будет, если 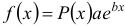 , где
, где 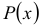 — многочлен.
— многочлен.
Пример №2
Решить уравнение 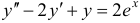 .
.
Решение:
Имеем: 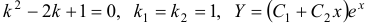 . Так как в характеристическом уравнении корень имеет кратность, равную двум, то частное решение данного уравнения ищем в виде
. Так как в характеристическом уравнении корень имеет кратность, равную двум, то частное решение данного уравнения ищем в виде 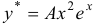 . Далее имеем:
. Далее имеем:
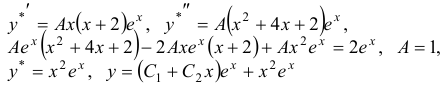
в) 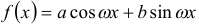 (
(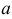 и
и 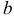 не нули одновременно). В этом случае частное решение у ищем также в форме тригонометрического двучлена
не нули одновременно). В этом случае частное решение у ищем также в форме тригонометрического двучлена 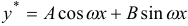 , где
, где 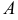 и
и 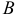 — неопределенные коэффициенты.
— неопределенные коэффициенты.
В случае 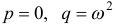 (или когда
(или когда 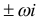 — корни характеристического уравнения) частное решение исходного уравнения ищем в виде
— корни характеристического уравнения) частное решение исходного уравнения ищем в виде 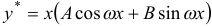 .
.
Пример №3
Решить уравнение 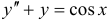 .
.
Решение:
Имеем: 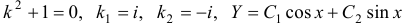 . Так как
. Так как 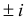 — корни характеристического уравнения, то частное решение данного уравнения ищем в виде
— корни характеристического уравнения, то частное решение данного уравнения ищем в виде 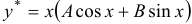 . Далее имеем:
. Далее имеем:
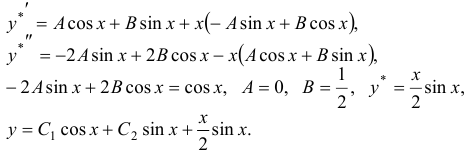
Для рассматриваемых дифференциальных уравнений справедлива так называемая теорема наложения, которая позволяет отыскивать частное решение в более сложных случаях.
Теорема. Если 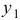 является решением уравнения
является решением уравнения 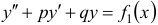 , а
, а 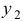 решением уравнения
решением уравнения 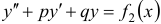 , то
, то 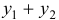 есть решение уравнения
есть решение уравнения 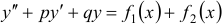 .
.
Пример №4
Найти общее решение уравнения 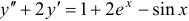 .
.
Решение:
Характеристическое уравнение 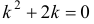 имеет корни
имеет корни 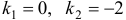 . Следовательно,
. Следовательно, 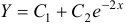 . Находим частное решение
. Находим частное решение 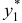 уравнения
уравнения 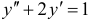 в виде
в виде 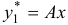 , тогда
, тогда 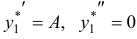 . Отсюда
. Отсюда 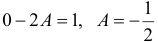 . Следовательно,
. Следовательно, 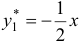 .
.
Частное решение 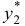 уравнения
уравнения 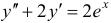 ищем в форме
ищем в форме 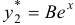 . Тогда
. Тогда 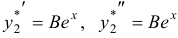 . Отсюда
. Отсюда 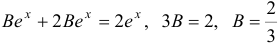 . Следовательно,
. Следовательно, 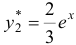 .
.
Наконец, находим частное решение 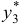 уравнения
уравнения 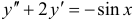 в форме
в форме 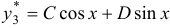 , тогда
, тогда 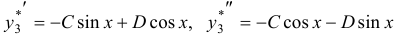 . Подставляя в уравнение, получим:
. Подставляя в уравнение, получим: 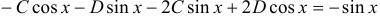 . Отсюда имеем:
. Отсюда имеем: 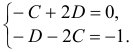 Значит
Значит 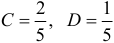 . Следовательно,
. Следовательно, 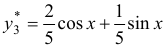 .
.
По теореме наложения частное решение исходного уравнения будет: 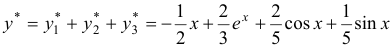 , тогда общее решение запишется так:
, тогда общее решение запишется так: 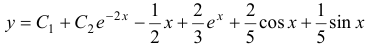 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Уравнения, не содержащие x |
| Линейные однородные уравнения с постоянными коэффициентами |
| Метод вариации произвольных постоянных |
| Сведение системы к одному дифференциальному уравнению высшего порядка |

