Оглавление:
В теории вероятностей первичными понятиями являются испытания и события. Пусть проводится некоторое испытание со случайным исходом. Множество всех возможных взаимоисключающих исходов данного испытания называется множеством элементарных событий. Совокупность всех элементарных событий называется достоверным событием. Всякое подмножество множества элементарных событий называется случайным событием.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Теория вероятностей
Теория вероятностей – математическая наука, изучающая закономерности, присущие массовым случайным явлениям.
Курсовые работы на темы: Вероятностные пространства. Элементы комбинаторики
В теории вероятностей часто приходится иметь дело с задачами, в которых необходимо подсчитывать число возможных способов совершения каких-либо действий. Задачи такого типа называются комбинаторными, а раздел математики, занимающийся решением таких задач, — комбинаторикой. Сформулируем два универсальных правила, применяемых при решении комбинаторных задач.
Правило произведения. Пусть требуется выполнить одно за другим какие-либо 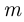 действий. Если первое действие можно выполнить
действий. Если первое действие можно выполнить 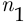 способами, второе действие —
способами, второе действие — 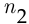 способами и так до
способами и так до 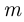 -го действия, которое можно выполнить
-го действия, которое можно выполнить 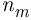 способами, то все
способами, то все 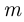 действий могут быть выполнены
действий могут быть выполнены 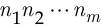 способами.
способами.
Правило суммы. Пусть требуется выполнить одно из каких-либо 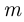 действий, взаимно исключающих друг друга. Если первое действие можно выполнить
действий, взаимно исключающих друг друга. Если первое действие можно выполнить 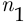 способами, второе действие —
способами, второе действие — 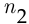 способами и так до
способами и так до 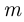 -го действия, которое можно выполнить
-го действия, которое можно выполнить 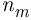 способами, то выполнить одно из этих
способами, то выполнить одно из этих 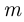 действий можно
действий можно 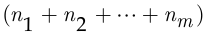 способами.
способами.
Напомним понятие факториала, активно используемое в комбинаторике. Факториалом натурального числа 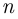 называется число
называется число
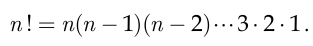
По определению, факториалом нуля является единица:
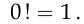
Рассмотрим некоторое множество 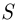 , состоящее из
, состоящее из 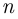 различных элементов. Пусть
различных элементов. Пусть 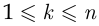 . Назовём множество, состоящее из
. Назовём множество, состоящее из 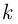 элементов, упорядоченным, если каждому элементу этого множества поставлено в соответствие число от 1 до
элементов, упорядоченным, если каждому элементу этого множества поставлено в соответствие число от 1 до 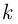 , причём различным элементам множества соответствуют разные числа.
, причём различным элементам множества соответствуют разные числа.
Размещениями из 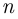 элементов по к называются упорядоченные подмножества множества
элементов по к называются упорядоченные подмножества множества 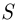 , состоящие из
, состоящие из 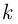 различных элементов и отличающиеся друг от друга составом элементов или порядком их расположения.
различных элементов и отличающиеся друг от друга составом элементов или порядком их расположения.
Число размещений из 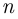 элементов по
элементов по 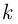 равно
равно
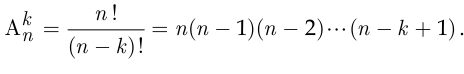
Перестановками из 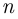 элементов называются размещения из
элементов называются размещения из 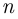 элементов по
элементов по 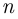 , т.е. упорядоченные подмножества множества
, т.е. упорядоченные подмножества множества 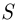 , состоящие из всех элементов данного множества и отличающиеся друг от друга только порядком их расположения.
, состоящие из всех элементов данного множества и отличающиеся друг от друга только порядком их расположения.
Число перестановок из 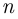 элементов равно
элементов равно
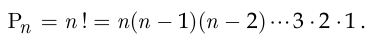
Сочетаниями из 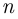 элементов по
элементов по 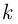 называются подмножества множества
называются подмножества множества 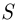 , состоящие из
, состоящие из 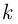 различных элементов и отличающиеся друг от друга только составом элементов.
различных элементов и отличающиеся друг от друга только составом элементов.
Число сочетаний из 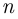 элементов по
элементов по 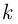 равно
равно
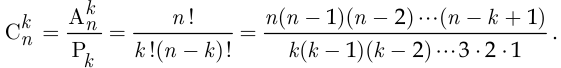
Размещениями с повторениями из 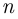 элементов по
элементов по 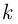 называются упорядоченные подмножества множества
называются упорядоченные подмножества множества 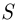 , состоящие из
, состоящие из 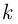 элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга составом элементов или порядком их расположения.
элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга составом элементов или порядком их расположения.
Число размещений с повторениями из 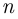 элементов по
элементов по 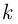 равно
равно
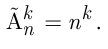
Сочетаниями с повторениями из 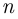 элементов по
элементов по 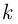 называются подмножества множества
называются подмножества множества 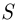 , состоящие из
, состоящие из 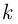 элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга только составом элементов.
элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга только составом элементов.
Число сочетаний с повторениями из 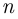 элементов по
элементов по 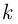 равно
равно
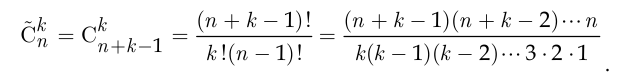
Отметим, что формулы (1.4) — (1.7) сохраняют смысл и остаются справедливыми и при 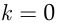 . Если во множестве
. Если во множестве 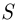 , состоящем из
, состоящем из 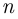 элементов, есть только
элементов, есть только 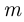 различных элементов, то перестановками с повторениями из
различных элементов, то перестановками с повторениями из 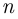 элементов называются упорядоченные подмножества множества
элементов называются упорядоченные подмножества множества 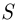 , в которые первый элемент множества
, в которые первый элемент множества 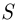 входит
входит 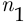 раз, второй элемент —
раз, второй элемент — 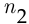 раз и так до
раз и так до 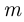 -го элемента, который входит
-го элемента, который входит 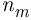 раз
раз  .
.
Число перестановок с повторениями из 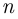 элементов, в которые первый элемент множества
элементов, в которые первый элемент множества 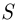 входит
входит 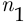 раз, второй элемент —
раз, второй элемент — 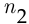 раз и так до
раз и так до 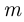 -го элемента, который входит
-го элемента, который входит 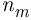 раз
раз  , равно
, равно
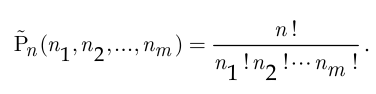
Курсовая работа №1
- Маша поссорилась с Петей и не хочет ехать с ним в одном автобусе. От общежития до института с 7 до 8 ч отправляется пять автобусов. Не успевший на последний из этих автобусов опаздывает на лекцию. Сколькими способами Маша и Петя могут доехать до института в разных автобусах и не опоздать на лекцию?
Решение:
Петя может доехать до института 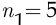 различными способами (на одном из пяти автобусов), при этом Маше остаётся только
различными способами (на одном из пяти автобусов), при этом Маше остаётся только 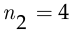 способа (так как один из автобусов занят Петей). Таким образом, по правилу произведения у Пети и Маши есть
способа (так как один из автобусов занят Петей). Таким образом, по правилу произведения у Пети и Маши есть 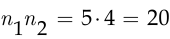 различных способов добраться до института в разных автобусах и не опоздать на лекцию. □
различных способов добраться до института в разных автобусах и не опоздать на лекцию. □
- В информационно-технологическом управлении банка работают три аналитика, десять программистов и 20 инженеров. Для сверхурочной работы в праздничный день начальник управления должен выделить одного сотрудника. Сколько способов существует у начальника управления?
Курсовая работа №2
Решение:
Начальник управления может отобрать одного аналитика 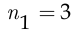 способами, одного программиста —
способами, одного программиста — 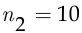 способами, а одного инженера —
способами, а одного инженера — 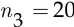 способами. Поскольку по условию задачи начальник управления может выделить любого из своих сотрудников, согласно правилу суммы у него существует
способами. Поскольку по условию задачи начальник управления может выделить любого из своих сотрудников, согласно правилу суммы у него существует 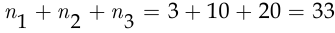 различных способа выбрать сотрудника для сверхурочной работы. □
различных способа выбрать сотрудника для сверхурочной работы. □
Курсовая работа №3
- Начальник службы безопасности банка должен ежедневно расставлять десять охранников по десяти постам. В целях усиления безопасности одна и та же комбинация расстановки охранников по постам не может повторяться чаще одного раза в месяц. Чтобы оценить, возможно ли это, найти число различных комбинаций расстановки охранников.
Решение:
Первый способ. На первый пост начальник службы безопасности может назначить любого из 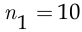 охранников, на второй пост — любого из оставшихся
охранников, на второй пост — любого из оставшихся 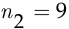 охранников и так до девятого поста, на который можно назначить любого из оставшихся
охранников и так до девятого поста, на который можно назначить любого из оставшихся 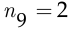 охранников, при этом оставшийся
охранников, при этом оставшийся 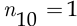 охранник будет назначен на десятый пост. Поэтому, согласно правилу произведения, у начальника службы безопасности есть
охранник будет назначен на десятый пост. Поэтому, согласно правилу произведения, у начальника службы безопасности есть 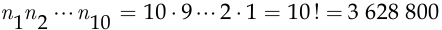 способов расстановки охранников по постам. Поскольку количество дней в месяце не превышает 31, у начальника службы безопасности заведомо существует достаточное число способов расстановки своих подчинённых по постам.
способов расстановки охранников по постам. Поскольку количество дней в месяце не превышает 31, у начальника службы безопасности заведомо существует достаточное число способов расстановки своих подчинённых по постам.
Второй способ. Число способов расстановки десяти охранников по десяти постам, существующих у начальника службы безопасности, описывается числом перестановок из 10 элементов, т. е. 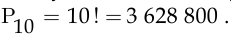 □
□
Курсовая работа №4
- Новый президент банка должен назначить двух новых вице-президентов из числа десяти директоров. Сколько способов существует у президента, если: а) один из вице-президентов (первый) выше другого по должности; б) вице-президенты по должности равны между собой.
Решение:
Первый способ, а) Первого вице-президента можно выбрать из 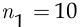 претендентов, при этом на пост второго вице-президента будут претендовать
претендентов, при этом на пост второго вице-президента будут претендовать 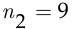 оставшихся директоров. Поэтому, согласно правилу произведения, у нового президента банка есть
оставшихся директоров. Поэтому, согласно правилу произведения, у нового президента банка есть 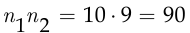 способов назначения двух вице-президентов, один из которых подчиняется другому, из числа десяти директоров, б) Пусть первое действие заключается в том, что президент отбирает двух человек на должности вице-президентов, а второе действие — в том, что президент говорит отобранным людям, кто из них является первым вице-президентом, а кто — вторым. Пусть первое действие можно выполнить
способов назначения двух вице-президентов, один из которых подчиняется другому, из числа десяти директоров, б) Пусть первое действие заключается в том, что президент отбирает двух человек на должности вице-президентов, а второе действие — в том, что президент говорит отобранным людям, кто из них является первым вице-президентом, а кто — вторым. Пусть первое действие можно выполнить 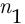 способами, второе действие, очевидно, можно выполнить
способами, второе действие, очевидно, можно выполнить 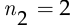 способами, и по правилу произведения число способов назначения двух вице-президентов, один из которых подчиняется другому, из числа десяти директоров составляет
способами, и по правилу произведения число способов назначения двух вице-президентов, один из которых подчиняется другому, из числа десяти директоров составляет 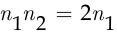 . С другой стороны, в пункте а) мы нашли это число, и оно оказалось равным 90, поэтому
. С другой стороны, в пункте а) мы нашли это число, и оно оказалось равным 90, поэтому 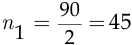 .
.
Второй способ, а) Число способов выбора двух кандидатов на две различные должности из десяти претендентов описывается числом размещений из 10 элементов по 2, т. е. 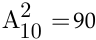 . б) Число способов выбора двух кандидатов на две одинаковые должности из десяти претендентов описывается числом сочетаний из 10 элементов по 2, т. е.
. б) Число способов выбора двух кандидатов на две одинаковые должности из десяти претендентов описывается числом сочетаний из 10 элементов по 2, т. е. 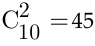 . □
. □
Курсовая работа №5
- Маша очень любит пирожные и ежедневно в булочной рядом с институтом покупает шесть пирожных (одинаковых или разных). Всего в булочной продаётся 11 сортов пирожных. Сколькими способами Маша может выбрать из них шесть штук?
Решение:
Каждому набору пирожных, которые выберет Маша, будем ставить в соответствие последовательность нулей и единиц, определяемую по следующему правилу. Напишем подряд столько единиц, сколько пирожных первого вида выбрала Маша, далее поставим нуль и после него запишем количество отобранных пирожных второго вида и т. д. Например, комбинации «одно пирожное второго вида, три пирожных пятого вида и одно пирожное восьмого вида» соответствует такая последовательность: «010001110001000» (нули отделяют виды пирожных друг от друга, поэтому нуль после одиннадцатого вида не нужен). При этом каждому набору пирожных взаимно однозначным образом соответствует последовательность, построенная по описанному правилу. Все такие последовательности состоят, очевидно, из 16 знаков, причём 10 из них нули, которые могут занимать любое место. Поэтому количество способов выбора пирожных равно количеству всех таких последовательностей, т. е. числу размещений десяти нулей по 16 местам: 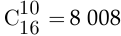 . □
. □
Курсовая работа №6
- Сколько различных слов можно составить, переставляя буквы в слове «мама»? Выписать все эти слова.
Решение:
Число различных слов, которые можно составить, переставляя буквы в слове «мама», описывается числом перестановок с повторениями из 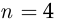 элементов (букв в слове «мама»), в которые первый элемент (буква «м») входит
элементов (букв в слове «мама»), в которые первый элемент (буква «м») входит 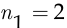 раза, а второй элемент (буква «а») —
раза, а второй элемент (буква «а») — 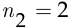 раза
раза 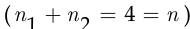 . Это число равно
. Это число равно 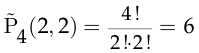 . Шесть различных слов, получающиеся перестановками букв в слове «мама», таковы: «ммаа», «мама», «маам», «амма», «амам», «аамм».
. Шесть различных слов, получающиеся перестановками букв в слове «мама», таковы: «ммаа», «мама», «маам», «амма», «амам», «аамм».
Курсовые работы на темы: Исчисление событий
Случайное событие  , связанное с опытом
, связанное с опытом 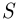 , — это такое событие, которое может произойти или не произойти в результате опыта
, — это такое событие, которое может произойти или не произойти в результате опыта 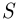 , причём заранее, до проведения опыта, неизвестно, произойдёт оно или нет. Всюду в дальнейшем при рассмотрении случайных событий мы будем опускать слово «случайное». Достоверным событием, связанным с опытом
, причём заранее, до проведения опыта, неизвестно, произойдёт оно или нет. Всюду в дальнейшем при рассмотрении случайных событий мы будем опускать слово «случайное». Достоверным событием, связанным с опытом 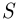 , называется такое событие
, называется такое событие 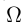 , которое обязательно произойдёт в результате опыта
, которое обязательно произойдёт в результате опыта 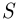 . Невозможным событием, связанным с опытом
. Невозможным событием, связанным с опытом 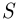 , называется такое событие
, называется такое событие 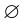 , которое обязательно не произойдёт в результате опыта
, которое обязательно не произойдёт в результате опыта 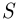 .
.
Над событиями  и
и  , связанными с одним и тем же опытом
, связанными с одним и тем же опытом 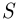 , определены следующие операции.
, определены следующие операции.
Событие  влечёт за собой событие
влечёт за собой событие  (или событие
(или событие  вложено в событие
вложено в событие  ), если каждое появление события
), если каждое появление события  сопровождается появлением события
сопровождается появлением события  . Это обозначается как
. Это обозначается как 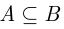 . События
. События  и
и  называют эквивалентными, если
называют эквивалентными, если 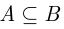 и
и 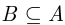 . Эквивалентность обозначается как
. Эквивалентность обозначается как 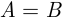 .
.
Объединением (или суммой) событий  и
и  называется событие
называется событие  (или
(или 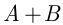 ), которое наступает всегда, когда наступает либо событие
), которое наступает всегда, когда наступает либо событие  , либо событие
, либо событие  .
.
Пересечением (или произведением) событий  и
и  называется событие
называется событие 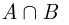 (или
(или 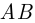 ), которое наступает всегда, когда события
), которое наступает всегда, когда события  и
и  наступают одновременно.
наступают одновременно.
Дополнением события  до события
до события  (или разностью событий
(или разностью событий  и
и  ) называется событие
) называется событие 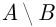 , которое наступает всегда, когда наступает событие
, которое наступает всегда, когда наступает событие  , и при этом не наступает событие
, и при этом не наступает событие  .
.
Противоположным событию  называется событие
называется событие 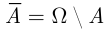 (читается «не
(читается «не  »), которое наступает всегда, когда событие А не наступает.
»), которое наступает всегда, когда событие А не наступает.
События  и
и  называются несовместными, если
называются несовместными, если 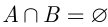 , т. е. если в результате опыта события
, т. е. если в результате опыта события  и
и  не могут наступить одновременно.
не могут наступить одновременно.
Говорят, что события 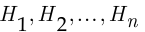 образуют полную группу, если они попарно несовместны
образуют полную группу, если они попарно несовместны 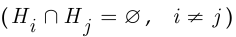 и их объединение эквивалентно достоверному событию
и их объединение эквивалентно достоверному событию 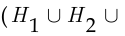
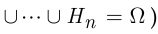 .
.
Случайное событие 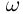 , связанное с опытом
, связанное с опытом 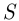 , которое невозможно представить как объединение или пересечение более простых событий, связанных с тем же опытом, называется элементарным событием. Очевидно, достоверное событие
, которое невозможно представить как объединение или пересечение более простых событий, связанных с тем же опытом, называется элементарным событием. Очевидно, достоверное событие 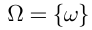 — это множество всех элементарных событий (поэтому
— это множество всех элементарных событий (поэтому 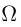 называют ещё пространством элементарных событий), а невозможное событие
называют ещё пространством элементарных событий), а невозможное событие 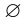 — это пустое множество. Любое событие, связанное с опытом
— это пустое множество. Любое событие, связанное с опытом 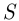 , можно представить как некоторое подмножество достоверного события
, можно представить как некоторое подмножество достоверного события 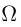 , т. е. как множество некоторых элементарных событий.
, т. е. как множество некоторых элементарных событий.
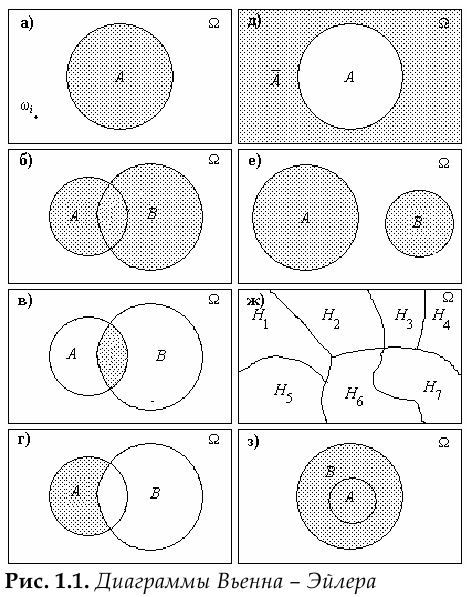
Для наглядного представления событий, операций над событиями и отношений между ними используются диаграммы Вьенна — Эйлера (рис. 1.1). На этих диаграммах достоверное событие 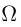 изображается в виде некоторой области на плоскости, элементарные события
изображается в виде некоторой области на плоскости, элементарные события 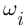 — точками внутри области, соответствующей
— точками внутри области, соответствующей 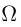 . При этом любому случайному событию
. При этом любому случайному событию  будет соответствовать некоторая геометрическая фигура внутри области, соответствующей
будет соответствовать некоторая геометрическая фигура внутри области, соответствующей 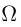 (рис- 1-1а). Объединение
(рис- 1-1а). Объединение  событий
событий  и
и  состоит из всех элементарных событий, принадлежащих, по крайней мере, одному из событий
состоит из всех элементарных событий, принадлежащих, по крайней мере, одному из событий  и
и  (рис. 1.16). Пересечение
(рис. 1.16). Пересечение 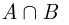 событий
событий  и
и  состоит из всех элементарных событий, принадлежащих одновременно обоим событиям
состоит из всех элементарных событий, принадлежащих одновременно обоим событиям  и
и  (рис. 1.1в). Дополнение
(рис. 1.1в). Дополнение 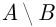 события
события  до события
до события  состоит из всех элементарных событий, принадлежащих событию А и при этом не принадлежащих событию
состоит из всех элементарных событий, принадлежащих событию А и при этом не принадлежащих событию  (рис. 1.1г). Событие
(рис. 1.1г). Событие  , противоположное событию
, противоположное событию  , состоит из всех элементарных событий, не принадлежащих событию
, состоит из всех элементарных событий, не принадлежащих событию  (рис. 1.1д). Несовместные события не имеют общих элементарных событий (рис. l.le). Полная группа событий представлена на рис. 1.1ж. Событие
(рис. 1.1д). Несовместные события не имеют общих элементарных событий (рис. l.le). Полная группа событий представлена на рис. 1.1ж. Событие  влечёт за собой событие
влечёт за собой событие  , если все элементарные события, входящие в
, если все элементарные события, входящие в  , входят и в
, входят и в  (рис. 1.1з).
(рис. 1.1з).
Курсовая работа №7
Операции над событиями обладают следующими свойствами:

Известно, что 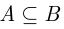 . Найти
. Найти
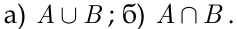
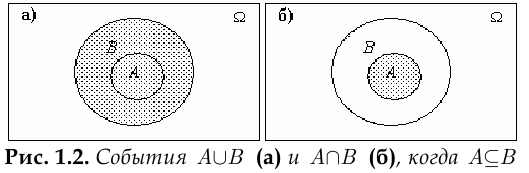
Решение. Событие  заштриховано на рис. 1.2а, событие
заштриховано на рис. 1.2а, событие 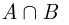 — на рис. 1.2б, откуда следует, очевидно, что
— на рис. 1.2б, откуда следует, очевидно, что
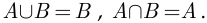
Курсовая работа №8
- Проверить, являются ли события
 и
и 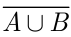 (где
(где  и
и  — произвольные события) несовместными.
— произвольные события) несовместными.
Решение:
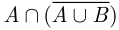 = {по правилу де Моргана} =
= {по правилу де Моргана} = 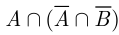 = {по свойству ассоциативности пересечения} =
= {по свойству ассоциативности пересечения} = 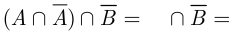 = , значит, события
= , значит, события  и
и 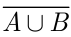 являются несовместными.
являются несовместными.
Курсовые работы на темы: Классическое определение вероятности
Вероятность наступления события характеризует меру возможности наступления этого события при проведении опыта. Если множество элементарных событий 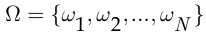 конечно, и все элементарные события одинаково возможны, то такая вероятностная схема носит название классической. В этом случае вероятность
конечно, и все элементарные события одинаково возможны, то такая вероятностная схема носит название классической. В этом случае вероятность 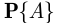 наступления события
наступления события 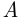 , состоящего из
, состоящего из 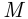 элементарных событий, входящих в
элементарных событий, входящих в 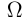 , определяется как отношение числа
, определяется как отношение числа 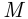 элементарных событий, благоприятствующих наступлению события
элементарных событий, благоприятствующих наступлению события 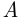 , к общему числу
, к общему числу 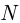 элементарных событий. Эта формула носит название классического определения вероятности:
элементарных событий. Эта формула носит название классического определения вероятности:
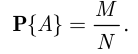
В частности, согласно классическому определению вероятности,
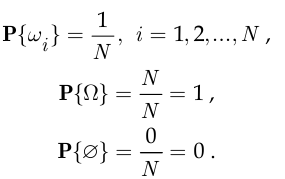
Частным случаем классической вероятностной схемы является урновая схема: в урне содержится 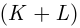 шаров, среди которых
шаров, среди которых 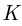 белых и
белых и 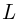 чёрных; из урны наугад без возвращения извлекаются
чёрных; из урны наугад без возвращения извлекаются 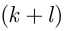 шаров, тогда вероятность
шаров, тогда вероятность 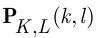 того, что в выборке содержится ровно
того, что в выборке содержится ровно 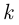 белых шаров и
белых шаров и 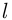 чёрных, вычисляется по формуле гипергеометрической вероятности:
чёрных, вычисляется по формуле гипергеометрической вероятности:
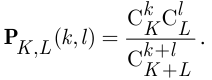
В случае, когда множество элементарных событий бесконечно и даже несчётно (но эти события являются одинаково возможными), вероятность наступления события можно рассчитать, пользуясь геометрическим определением вероятности, которое состоит в следующем. Пусть множество элементарных событий 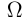 представляет собой некоторую область в
представляет собой некоторую область в 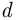 -мерном пространстве, имеющую ненулевой объём:
-мерном пространстве, имеющую ненулевой объём:
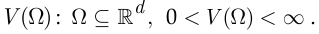
При этом каждому элементарному событию соответствует точка
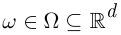
а каждое событие 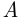 представляет собой область, вложенную в
представляет собой область, вложенную в 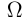 и имеющую объём
и имеющую объём
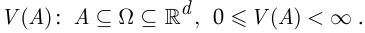
Тогда, согласно геометрическому определению вероятности, вероятность 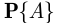 наступления события
наступления события 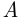 можно рассчитать как отношение объёма
можно рассчитать как отношение объёма 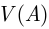 области
области 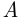 к объёму
к объёму 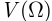 области
области 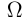 :
:
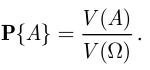
Если элементарные события не являются одинаково возможными, для приближённого вычисления вероятностей можно использовать относительные частоты. Пусть в результате 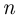 -кратного проведения опыта
-кратного проведения опыта 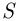 событие
событие 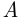 наступило
наступило 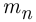 раз. Назовём относительной частотой
раз. Назовём относительной частотой 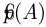 появления события
появления события 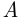 в серии из
в серии из 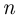 опытов
опытов 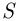 отношение числа
отношение числа 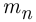 наступлений события
наступлений события 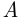 к общему числу
к общему числу 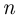 проведённых опытов:
проведённых опытов:
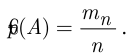
При этом вероятность 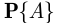 наступления события
наступления события 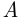 будет равна пределу относительной частоты наступления этого события в серии из
будет равна пределу относительной частоты наступления этого события в серии из 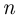 опытов при неограниченном увеличении числа опытов:
опытов при неограниченном увеличении числа опытов:
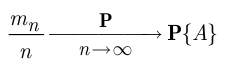
На практике в этом случае вероятность рассчитывают при помощи приближённого равенства
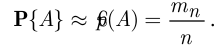
Курсовая работа №9
- В корзине три красных и семь зелёных яблок. Из корзины вынимают одно яблоко. Найти вероятность того, что оно будет красным.
Решение:
Пусть опытом будет извлечение яблока из корзины, а событие 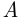 состоит в том, что извлечённое из корзины яблоко окажется красным. Тогда общее число элементарных событий
состоит в том, что извлечённое из корзины яблоко окажется красным. Тогда общее число элементарных событий 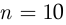 , из которых
, из которых 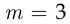 элементарных события благоприятствуют наступлению события
элементарных события благоприятствуют наступлению события 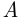 .
.
Согласно классическому определению вероятности
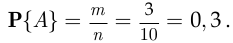
Курсовая работа №10
- Трое играют в карты. Каждому игроку сдано но десять карт и две оставлены в прикупе. Один из игроков видит, что у него на руках шесть карт бубновой масти, а четыре — других мастей. Он сбрасывает две карты из этих четырёх и берёт себе прикуп. Найти вероятность того, что в прикупе окажутся две бубновые карты.
Решение:
Пусть событие 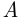 состоит в том, что в прикупе окажутся две бубновые карты. Из 32 карт игроку известны десять, а остальные 22 неизвестны. Взять две карты из прикупа — это то же самое, что взять их из 22 неизвестных карт, среди которых две бубновые. Поэтому общее число элементарных событий
состоит в том, что в прикупе окажутся две бубновые карты. Из 32 карт игроку известны десять, а остальные 22 неизвестны. Взять две карты из прикупа — это то же самое, что взять их из 22 неизвестных карт, среди которых две бубновые. Поэтому общее число элементарных событий 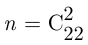 , из которых лишь
, из которых лишь 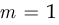 элементарное событие благоприятствует наступлению события
элементарное событие благоприятствует наступлению события 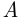 . Согласно классическому определению вероятности,
. Согласно классическому определению вероятности,
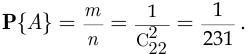
Курсовая работа №11
- В партии, состоящей из 1 ООО изделий, четыре изделия имеют дефекты. Для контроля отбираются 100 изделий. Найти вероятность того, что среди отобранных изделий не окажется бракованных.
Решение:
По формуле гипергеометрической вероятности (1.31)
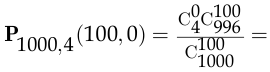

Курсовая работа №12
- Двери лифта закрылись на первом этаже прямо перед Петей, который успел только заметить, что в лифт вошли шесть человек. В общежитии семь этажей, и лифт, если откроет на каком-либо из них двери, стоит там целую минуту. Петя живёт на седьмом этаже и очень не хочет идти по лестнице. Он размышляет, каковы вероятности следующих событий: а) все шестеро выйдут на одном этаже; б) все шестеро выйдут на разных этажах. Найти эти вероятности.
Решение:
а) Опыт, за которым наблюдает Петя, состоит в том, что люди выходят из лифта произвольным образом: каждый из шести человек может выйти на любом из шести этажей (со второго по седьмой). Общее число исходов этого опыта 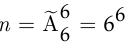 (первый человек может выйти на любом из шести этажей, второй — также на любом из шести этажей и так до шестого человека; все эти шесть шестёрок перемножаются по правилу произведения). Пусть событие
(первый человек может выйти на любом из шести этажей, второй — также на любом из шести этажей и так до шестого человека; все эти шесть шестёрок перемножаются по правилу произведения). Пусть событие 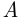 состоит в том, что все шесть человек выйдут на одном и том же этаже, тогда число исходов описанного опыта, благоприятствующих наступлению события
состоит в том, что все шесть человек выйдут на одном и том же этаже, тогда число исходов описанного опыта, благоприятствующих наступлению события 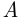 , равно
, равно 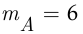 (всего есть шесть этажей).
(всего есть шесть этажей).
Поэтому, согласно классическому определению вероятности,
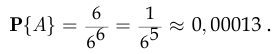
смотрим тот же опыт, что и в п. а). Пусть событие 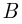 состоит в том, что все шесть человек выйдут на разных этажах, тогда число исходов опыта, благоприятствующих наступлению события
состоит в том, что все шесть человек выйдут на разных этажах, тогда число исходов опыта, благоприятствующих наступлению события 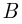 , равно
, равно 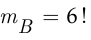 (число перестановок шести людей по шести этажам). По классической формуле вероятности
(число перестановок шести людей по шести этажам). По классической формуле вероятности
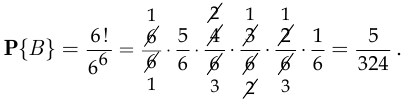
Курсовая работа №13
- Чтобы добраться в институт, Петя может воспользоваться автобусом одного из двух маршрутов. Автобусы первого маршрута следуют с интервалом в 18 мин, второго маршрута — с интервалом в 15 мин. Найти вероятность того, что Петя будет ждать автобуса не более 10 мин.

Решение:
Выберем в качестве множества элементарных событий  прямоугольник со сторонами
прямоугольник со сторонами 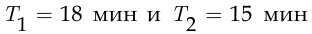 (рис. 1.3). Событие
(рис. 1.3). Событие 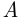 состоит в том, что время, которое Петя будет ждать автобуса, меньше
состоит в том, что время, которое Петя будет ждать автобуса, меньше 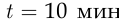 . Элементарные события, благоприятствующие наступлению события
. Элементарные события, благоприятствующие наступлению события 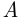 , заштрихованы на рис. 1.3. Поэтому, согласно геометрическому определению вероятности,
, заштрихованы на рис. 1.3. Поэтому, согласно геометрическому определению вероятности,
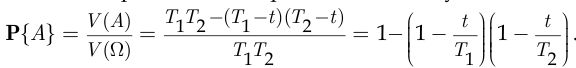
При
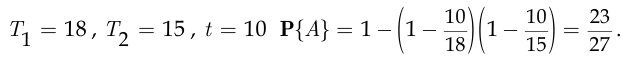
Курсовая работа №14
- Рыбаки поймали в пруду 100 рыб, окольцевали их и выпустили назад в воду. На следующий день они поймали 120 рыб, из которых 10 оказались окольцованными. Найти: а) вероятность того, что выловленная рыба окольцована; б) количество рыб в пруду.
Решение:
Пусть 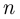 — число рыб в пруду,
— число рыб в пруду, 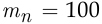 — число окольцованных рыб в пруду, событие
— число окольцованных рыб в пруду, событие 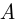 состоит в том, что выловленная рыба окольцована. Тогда вероятность события
состоит в том, что выловленная рыба окольцована. Тогда вероятность события 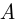 равна, согласно классическому определению,
равна, согласно классическому определению, 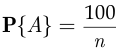 с другой стороны, поскольку из 120 выловленных рыб
с другой стороны, поскольку из 120 выловленных рыб 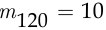 оказались окольцованы, вероятность события
оказались окольцованы, вероятность события 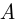 приближённо равна его относительной частоте:
приближённо равна его относительной частоте:
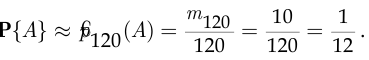
Отсюда
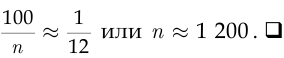
Курсовые работы на темы: Аксиоматическое построение теории вероятностей
Класс S подмножеств множества элементарных событий 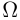 называется полем событий (алгеброй событий), если он содержит достоверное событие
называется полем событий (алгеброй событий), если он содержит достоверное событие 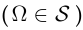 , а также замкнут относительно операций объединения (если
, а также замкнут относительно операций объединения (если 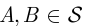 , то
, то 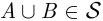 ), пересечения (если
), пересечения (если 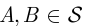 , то
, то 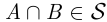 ) и дополнения (если
) и дополнения (если 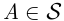 , то
, то 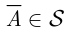 ). Поле событий
). Поле событий 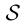 называется
называется 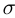 -полем (
-полем (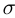 -алгеброй), если объединение и пересечение бесконечной (счётной) последовательности событий
-алгеброй), если объединение и пересечение бесконечной (счётной) последовательности событий 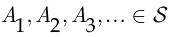 также принадлежат полю
также принадлежат полю 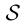 :
:
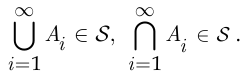
При аксиоматическом построении теории вероятностей в каждом конкретном пространстве элементарных событий 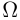 выделяется
выделяется 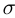 -поле событий
-поле событий 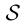 , и для каждого события
, и для каждого события 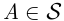 задаётся вероятность — числовая функция, определённая на
задаётся вероятность — числовая функция, определённая на 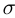 -поле событий
-поле событий 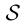 и удовлетворяющая следующим аксиомам.
и удовлетворяющая следующим аксиомам.
Аксиома неотрицательности вероятности:
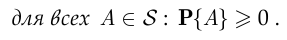
Аксиома нормированности вероятности:
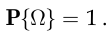
Аксиома аддитивности вероятности:
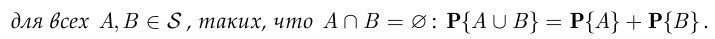
Во многих случаях вместо аксиомы аддитивности вероятности требуется её расширенный вариант, называемый аксиомой счётной аддитивности вероятности.
Аксиома счётной аддитивности вероятности:
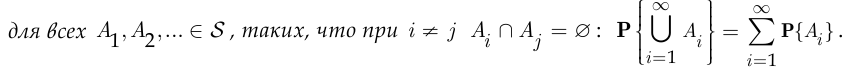
Каждая определённая теоретико-вероятностная схема задаётся тройкой 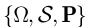 где
где 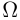 — конкретное пространство элементарных событий,
— конкретное пространство элементарных событий, 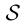 —
— 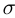 -поле событий, выделенное на
-поле событий, выделенное на 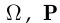 — вероятность, заданная на
— вероятность, заданная на 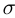 -поле
-поле 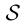 . Тройка
. Тройка 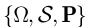 называется вероятностным пространством. Из аксиом (1.36) — (1.38) следуют следующие свойства вероятности:
называется вероятностным пространством. Из аксиом (1.36) — (1.38) следуют следующие свойства вероятности:
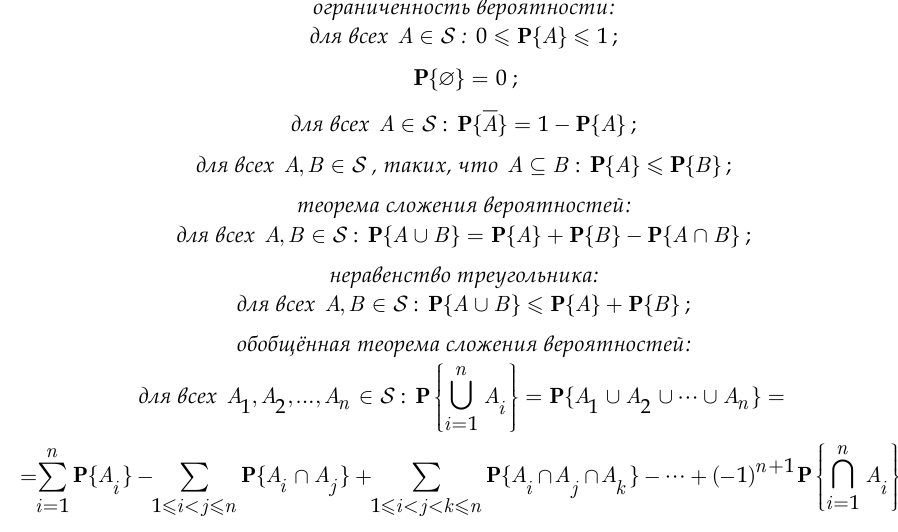
В случае 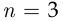 обобщённая теорема сложения вероятностей имеет следующий вид:
обобщённая теорема сложения вероятностей имеет следующий вид:
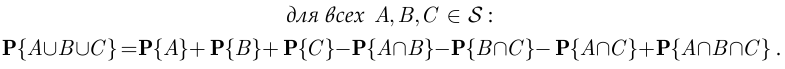
Курсовая работа №15
- Известно, что курс евро к рублю может возрасти с вероятностью 0,55, а курс доллара к рублю может возрасти с вероятностью 0,35. Вероятность того, что возрастут оба курса, составляет 0,3. Найти вероятность того, что курс евро или доллара но отношению к рублю возрастёт.
Решение:
Пусть событие 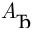 состоит в том, курс евро к рублю возрастёт, а событие
состоит в том, курс евро к рублю возрастёт, а событие 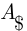 — в том, что курс доллара к рублю возрастёт. Тогда по условию
— в том, что курс доллара к рублю возрастёт. Тогда по условию
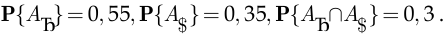
Вероятность того, что курс евро или доллара по отношению к рублю возрастёт, по теореме сложения вероятностей составляет
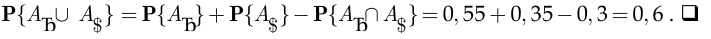
Курсовая работа №16
- Результаты опроса 1 000 случайно отобранных молодых людей таковы:

Определить, содержится ли в этой информации ошибка.
Решение:
Пусть событие 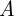 состоит в том, что случайно выбранный молодой человек работает, событие
состоит в том, что случайно выбранный молодой человек работает, событие 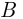 — в том, что случайно выбранный молодой человек проживает в Москве, событие
— в том, что случайно выбранный молодой человек проживает в Москве, событие 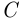 — в том, что случайно выбранный молодой человек учится. Так как
— в том, что случайно выбранный молодой человек учится. Так как 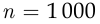 достаточно велико, можно воспользоваться статистическим определением вероятности:
достаточно велико, можно воспользоваться статистическим определением вероятности:
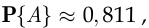
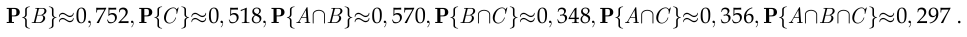
По формуле
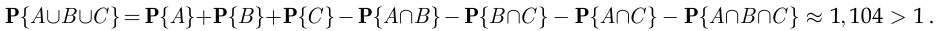
Но вероятность не может быть больше единицы, следовательно, в данной информации содержится ошибка. □
Курсовая работа №17
- Известно, что пять из сорока пассажиров самолёта замешаны в похищении крупной денежной суммы. В аэропорту к трапу самолёта подошёл инспектор уголовного розыска и заявил, что для обнаружения хотя бы одного преступника ему достаточно произвести обыск у шести наугад выбранных пассажиров. Что руководило инспектором: трезвый расчёт или риск?
Решение:
Пусть событие 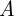 состоит в том, что среди шести случайно выбранных пассажиров есть хотя бы один преступник, событие
состоит в том, что среди шести случайно выбранных пассажиров есть хотя бы один преступник, событие 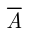 — в том, что среди шести случайно выбранных пассажиров нет ни одного преступника. Тогда, используя формулу гипергеометрической вероятности (1.31), в которой
— в том, что среди шести случайно выбранных пассажиров нет ни одного преступника. Тогда, используя формулу гипергеометрической вероятности (1.31), в которой
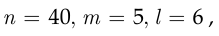
получим:
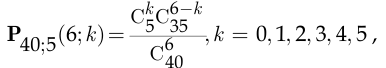
поэтому
С40 2 1
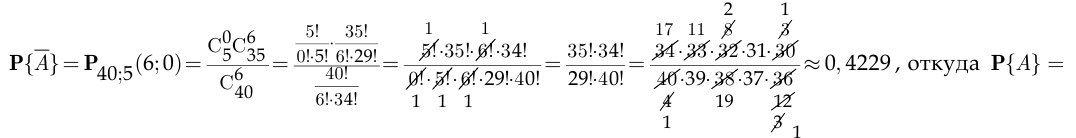
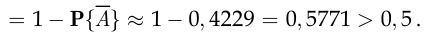
Видимо, это и побудило инспектора назвать число «шесть», хотя, на взгляд авторов, инспектор, скорее, рискует «пятьдесят на пятьдесят». □
Курсовая работа №18
- Доказать, что если класс
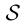 подмножеств множества элементарных событий замкнутый относительно операции дополнения, замкнут относительно операции объединения, то он замкнут и относительно операции пересечения.
подмножеств множества элементарных событий замкнутый относительно операции дополнения, замкнут относительно операции объединения, то он замкнут и относительно операции пересечения.
Решение:
По условию, если 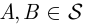 , то
, то 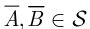 (так как
(так как 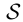 замкнут относительно операции дополнения). Так как
замкнут относительно операции дополнения). Так как 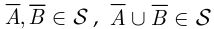 (так как
(так как 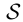 замкнут относительно операции объединения). Так как
замкнут относительно операции объединения). Так как 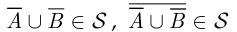 (так как
(так как 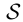 замкнут относительно операции дополнения). Но согласно правилу де Моргана
замкнут относительно операции дополнения). Но согласно правилу де Моргана 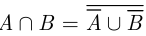 , поэтому
, поэтому 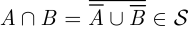 , т. е. класс
, т. е. класс 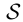 замкнут относительно операции пересечения. □
замкнут относительно операции пересечения. □
Курсовые работы на темы: Условные вероятности. Последовательности испытаний
Как уже было отмечено, говорить о вероятности наступления какого-либо события как о мере возможности наступления этого события можно лишь при выполнении определённого комплекса условий опыта. Так, если к комплексу условий, при которых изучалась вероятность наступления события 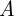 , добавить условие наступления события
, добавить условие наступления события 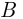 , получим другое значение вероятности
, получим другое значение вероятности 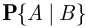 — вероятность наступления события
— вероятность наступления события 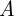 при условии, что событие
при условии, что событие 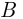 произошло (или условная вероятность события
произошло (или условная вероятность события 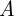 при условии
при условии 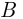 ), которая равна по определению
), которая равна по определению
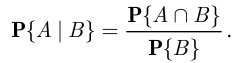
Иногда вместо обозначения 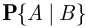 используют обозначение
используют обозначение
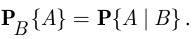
Вероятность 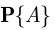 , в отличие от условной вероятности
, в отличие от условной вероятности 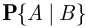 , называется безусловной. Из определения условной вероятности (2.1) следует формула умножения вероятностей
, называется безусловной. Из определения условной вероятности (2.1) следует формула умножения вероятностей
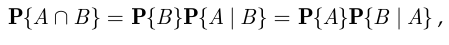
остающаяся справедливой и в случае, когда
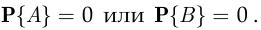
Говорят, что события 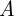 и
и 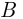 являются независимыми, если
являются независимыми, если
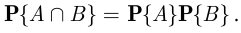
Формулу (2.3) для независимых событий 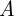 и
и 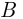 называют теоремой умножения вероятностей. Очевидно, при
называют теоремой умножения вероятностей. Очевидно, при 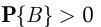 теорема умножения вероятностей (2.3) означает, что условная вероятность события
теорема умножения вероятностей (2.3) означает, что условная вероятность события 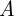 при условии
при условии 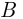 совпадает с безусловной вероятностью события
совпадает с безусловной вероятностью события 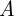 :
:
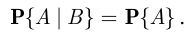
Формулу умножения вероятностей легко обобщить на случай произвольного конечного числа событий:
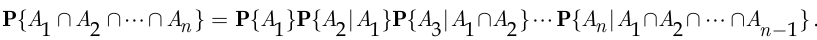
События 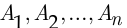 называются независимыми в совокупности, если для любого их подмножества
называются независимыми в совокупности, если для любого их подмножества 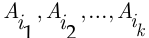 вероятность одновременного наступления событий
вероятность одновременного наступления событий 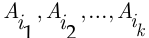 равна произведению безусловных вероятностей этих событий:
равна произведению безусловных вероятностей этих событий:
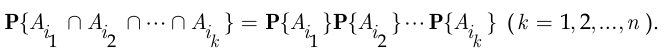
Если условие (2.6) выполняется только при 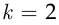 , то события
, то события 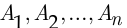 называются попарно независимыми.
называются попарно независимыми.
Следует обратить внимание на следующие факты:
• из условия несовместности не следует условие независимости;
• из условия независимости не следует условие несовместности;
• из условия независимости в совокупности следует попарная независимость, но из попарной независимости не следует независимость в совокупности.
Если события 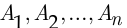 независимы в совокупности, то из обобщённой теоремы сложения вероятностей следует, что
независимы в совокупности, то из обобщённой теоремы сложения вероятностей следует, что
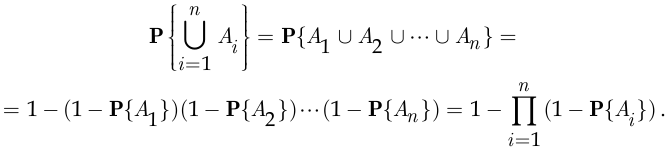
Если события 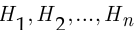 образуют полную группу, то для вычисления вероятности произвольного события
образуют полную группу, то для вычисления вероятности произвольного события 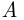 можно использовать формулу полной вероятности:
можно использовать формулу полной вероятности:
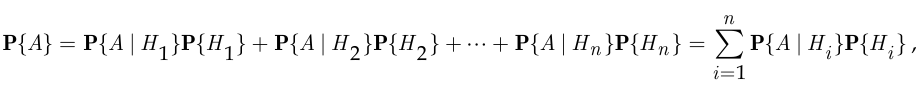
в соответствии с которой вероятность наступления события 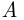 может быть представлена как сумма произведений условных вероятностей события
может быть представлена как сумма произведений условных вероятностей события 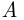 при условии наступления событий
при условии наступления событий 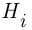 на безусловные вероятности этих событий
на безусловные вероятности этих событий 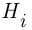 . Поскольку среди событий
. Поскольку среди событий 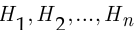 , образующих полную группу, в результате опыта должно наступить одно и только одно, эти события
, образующих полную группу, в результате опыта должно наступить одно и только одно, эти события 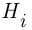 называют гипотезами
называют гипотезами
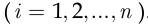
Формула полной вероятности (2.8) остаётся справедливой и в случае, если условие, состоящее в том, что события 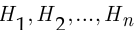 образуют полную группу, заменить более слабым: гипотезы
образуют полную группу, заменить более слабым: гипотезы 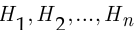 попарно несовместны
попарно несовместны 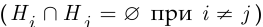 , а их объединение содержит событие
, а их объединение содержит событие
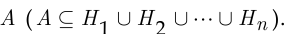
Из формулы полной вероятности следует формула Байеса:
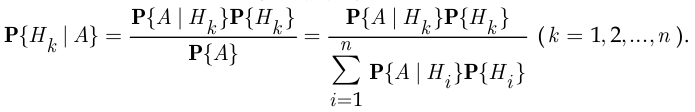
Вероятности 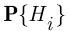 гипотез
гипотез 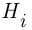 называют априорными вероятностями (вероятностями гипотез
называют априорными вероятностями (вероятностями гипотез 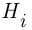 до проведения опыта) в отличие от апостериорных вероятностей
до проведения опыта) в отличие от апостериорных вероятностей 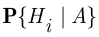 (вероятностей гипотез
(вероятностей гипотез 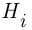 уточнённых в результате опыта, исходом которого стало событие
уточнённых в результате опыта, исходом которого стало событие 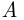 ).
).
Курсовая работа №19
- Известно, что
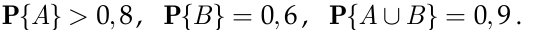
Найти
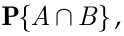
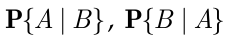
и выяснить, зависимы ли события 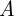 и
и 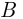 .
.
Решение:
По теореме сложения вероятностей
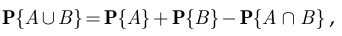
откуда
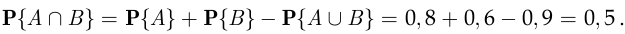
По определению условной вероятности
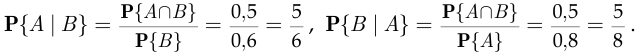
Для того, чтобы события 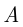 и
и 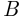 были независимыми, необходимо выполнение теоремы умножения вероятностей:
были независимыми, необходимо выполнение теоремы умножения вероятностей:
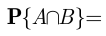
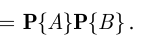
В нашем случае
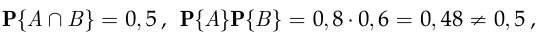
т. е. теорема умножения вероятностей не выполняется, значит, события 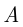 и
и 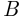 являются зависимыми. □
являются зависимыми. □
Курсовая работа №20
- Пусть события
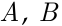 и
и 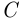 попарно независимы, причём каждое из них имеет вероятность, отличную от нуля и единицы. Проверить, могут ли события
попарно независимы, причём каждое из них имеет вероятность, отличную от нуля и единицы. Проверить, могут ли события 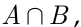
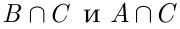 быть: а) попарно независимыми; б) независимыми в совокупности.
быть: а) попарно независимыми; б) независимыми в совокупности.
Решение:
а) Рассмотрим следующие события в условиях задачи 47: событие 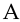 , заключающееся в том, что утечка газа происходит ближе к станции
, заключающееся в том, что утечка газа происходит ближе к станции 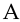 , чем к
, чем к 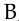 , событие
, событие 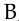 , заключающееся в том, что утечка расположена между 50-м и 150-м километрами, и событие
, заключающееся в том, что утечка расположена между 50-м и 150-м километрами, и событие 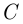 , состоящее в том, что утечка расположена между отметками 12,5 км и 62,5 км либо между 112,5 км и 162,5 км. Тогда, согласно геометрическому определению вероятности,
, состоящее в том, что утечка расположена между отметками 12,5 км и 62,5 км либо между 112,5 км и 162,5 км. Тогда, согласно геометрическому определению вероятности,
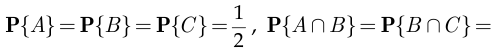
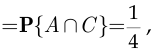
значит, события 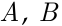 и
и 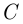 попарно независимы. При этом, очевидно,
попарно независимы. При этом, очевидно,
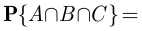
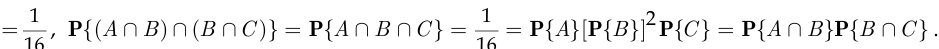
Аналогично получаем равенства
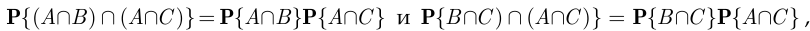
т. е. события 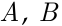 и
и 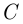 являются независимыми в совокупности, б) Независимость в совокупности означает, во-первых, что
являются независимыми в совокупности, б) Независимость в совокупности означает, во-первых, что
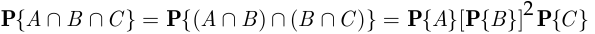
и, во-вторых, что
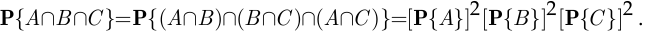
Поэтому
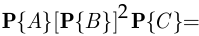
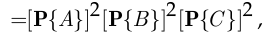
но это равенство невозможно, так как вероятности событий 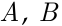 и
и 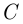 отличны от нуля и единицы. Поэтому события
отличны от нуля и единицы. Поэтому события
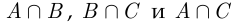
не могут быть независимыми в совокупности. □
Курсовая работа №21
- Статистика запросов кредитов в банке такова: 10% — государственные органы, 20% — другие банки, остальные — физические лица. Вероятности того, что взятый кредит не будет возвращён, составляют 0,01, 0,05 и 0,2 соответственно. Определить, какая доля кредитов в среднем не возвращается.
Решение:
Пусть событие 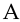 состоит в том, что взятый кредит не возвращается, гипотеза
состоит в том, что взятый кредит не возвращается, гипотеза 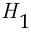 — в том, что запрос на этот кредит поступил от государственного органа, гипотеза
— в том, что запрос на этот кредит поступил от государственного органа, гипотеза 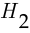 — в том, что запрос на кредит поступил от другого банка, гипотеза
— в том, что запрос на кредит поступил от другого банка, гипотеза 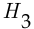 — в том, что запрос на кредит поступил от физического лица. По условию вероятности гипотез составляют
— в том, что запрос на кредит поступил от физического лица. По условию вероятности гипотез составляют
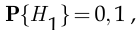
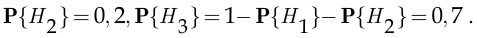
Апостериорные вероятности, в свою очередь, по условию равны
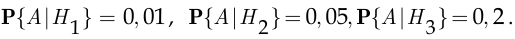
По формуле полной вероятности
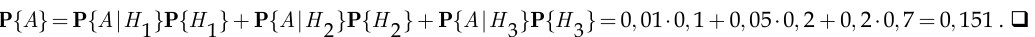
Курсовая работа №22
- В условиях задачи 105 начальнику кредитного отдела доложили, что получено факсимильное сообщение о неисполнении обязательств по возврату кредита, в котором очень плохо пропечаталось имя клиента. Найти вероятность того, что кредит не возвращает какой-либо банк.
Решение:
Пусть событие 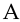 состоит в том, что взятый кредит не возвращается, гипотеза
состоит в том, что взятый кредит не возвращается, гипотеза 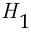 — в том, что запрос на этот кредит поступил от государственного органа, гипотеза
— в том, что запрос на этот кредит поступил от государственного органа, гипотеза 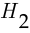 — в том, что запрос на кредит поступил от другого банка, гипотеза
— в том, что запрос на кредит поступил от другого банка, гипотеза 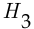 — в том, что запрос на кредит поступил от физического лица. По условию вероятности гипотез составляют
— в том, что запрос на кредит поступил от физического лица. По условию вероятности гипотез составляют
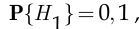
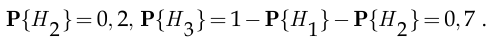
Апостериорные вероятности, в свою очередь, равны по условию
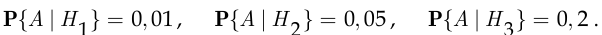
По формуле Байеса
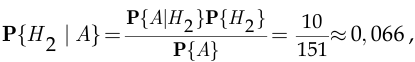
где вероятность
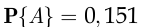
была рассчитана по формуле полной вероятности в задаче 105. □
Курсовая работа №23
Задача о разорении. Петя с папой играют в следующую игру. Петя бросает монету, предварительно сообщив папе, какая сторона, по его мнению, выпадет: «герб» или «решётка». Если Петя угадал, то папа платит Пете 1 руб., в противном случае Петя платит папе 1 руб. Начальный капитал Пети составляет 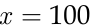 руб. Игра продолжается до тех пор, пока Петя не наберёт заранее определённую сумму
руб. Игра продолжается до тех пор, пока Петя не наберёт заранее определённую сумму 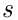 , либо пока он не разорится, проиграв весь имеющийся капитал
, либо пока он не разорится, проиграв весь имеющийся капитал 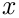 . Найти вероятность того, что Петя разорится, так и не набрав желаемую сумму, если эта сумма
. Найти вероятность того, что Петя разорится, так и не набрав желаемую сумму, если эта сумма 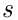 составляет: а) 110 руб; б) 1 000 руб.
составляет: а) 110 руб; б) 1 000 руб.
Решение:
Пусть 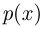 — вероятность того, что, имея
— вероятность того, что, имея 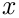 руб., Петя всё-таки разорится, событие
руб., Петя всё-таки разорится, событие 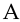 состоит в Петином разорении, гипотеза
состоит в Петином разорении, гипотеза 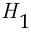 — в том, что Петя выиграл на первом шаге игры, гипотеза
— в том, что Петя выиграл на первом шаге игры, гипотеза 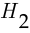 — в том, что Петя проиграл на первом шаге игры. При этом, очевидно, вероятность разорения при условии выигрыша на первом шаге составит
— в том, что Петя проиграл на первом шаге игры. При этом, очевидно, вероятность разорения при условии выигрыша на первом шаге составит
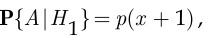
а вероятность разорения при условии проигрыша на первом шаге составит
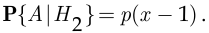
Согласно классическому определению вероятности
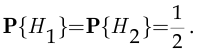
По формуле полной вероятности
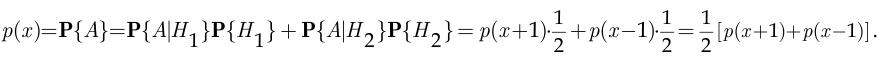
При этом, очевидно,
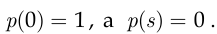
Решением уравнения
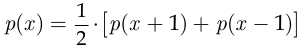
является линейная функция
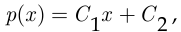
коэффициенты которой 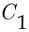 и
и 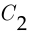 найдём из условий
найдём из условий
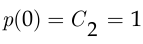
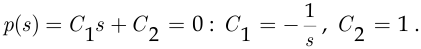
Таким образом,
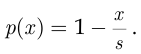
В случае а)
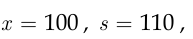
поэтому
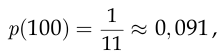
а в случае б)
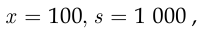
поэтому
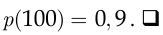
Курсовые работы на темы: Последовательности испытаний
Пусть проводится конечное число 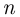 последовательных испытаний, в каждом из которых некоторое событие
последовательных испытаний, в каждом из которых некоторое событие 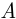 может либо наступить (такую ситуацию назовём успехом) либо не наступить (такую ситуацию назовём неудачей), причём эти испытания удовлетворяют следующим условиям:
может либо наступить (такую ситуацию назовём успехом) либо не наступить (такую ситуацию назовём неудачей), причём эти испытания удовлетворяют следующим условиям:
- каждое испытание случайно относительно события
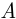 , т.е. до проведения испытания нельзя сказать, появится
, т.е. до проведения испытания нельзя сказать, появится 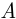 или нет;
или нет; - испытания проводятся в одинаковых, с вероятностной точки зрения, условиях, т. е. вероятность успеха в каждом отдельно взятом испытании равна
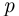 и не меняется от испытания к испытанию;
и не меняется от испытания к испытанию; - испытания независимы, т. е. события
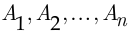 где
где 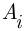 — состоит в успехе на
— состоит в успехе на 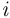 -м испытании
-м испытании 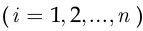 , независимы в совокупности.
, независимы в совокупности.
Такая последовательность испытаний называются схемой Бернулли или биномиальной схемой, а сами испытания — испытаниями Бернулли.
Вероятность 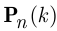 того, что в серии из
того, что в серии из 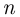 испытаний Бернулли окажется ровно
испытаний Бернулли окажется ровно 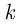 успешных, рассчитывается по формуле Бернулли:
успешных, рассчитывается по формуле Бернулли:
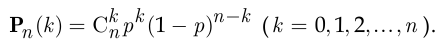
Наивероятнейшее число 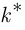 успехов в серии из
успехов в серии из 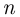 испытаний Бернулли удовлетворяет неравенствам
испытаний Бернулли удовлетворяет неравенствам
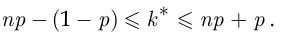
В случае, когда число 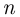 испытаний Бернулли велико, расчёты по формуле Бернулли становятся затруднительными. Если при этом вероятность
испытаний Бернулли велико, расчёты по формуле Бернулли становятся затруднительными. Если при этом вероятность 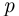 успеха в каждом испытании мала, так что можно считать, что
успеха в каждом испытании мала, так что можно считать, что
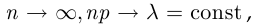
для расчёта 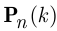 можно пользоваться приближённой формулой Пуассона:
можно пользоваться приближённой формулой Пуассона:
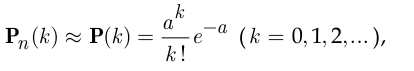
где
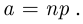
На практике формулой Пуассона пользуются в случае, когда число 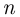 испытаний Бернулли — несколько десятков или более, а произведение
испытаний Бернулли — несколько десятков или более, а произведение 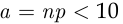 . В случае, когда
. В случае, когда 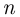 велико, а
велико, а 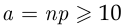 , формула Пуассона даёт очень грубое приближение, и для расчёта
, формула Пуассона даёт очень грубое приближение, и для расчёта 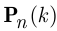 используют локальную и интегральную теоремы Муавра — Лапласа (см. §4.4).
используют локальную и интегральную теоремы Муавра — Лапласа (см. §4.4).
От схемы последовательных независимых испытаний с двумя исходами (биномиальной схемы) можно перейти к полиномиальной схеме, т. е. схеме последовательных независимых испытаний, в каждом из которых возможно 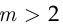 исходов с вероятностями
исходов с вероятностями 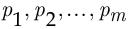 соответственно
соответственно
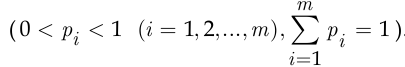
В полиномиальной схеме вероятность
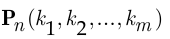
того, что в серии из 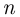 испытаний первый исход появится ровно
испытаний первый исход появится ровно 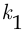 раз, второй исход появится ровно
раз, второй исход появится ровно 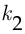 раз и так до
раз и так до 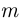 -го исхода, который появится ровно
-го исхода, который появится ровно 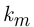 раз, рассчитывается по формуле
раз, рассчитывается по формуле
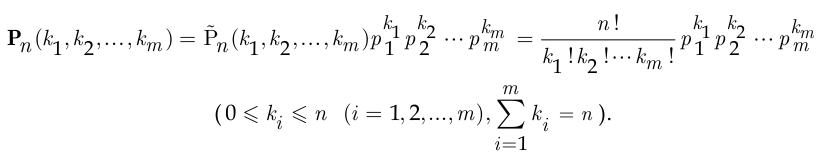
Курсовая работа №24
- Известно, что из числа зрителей определённой телепрограммы 70% смотрят и рекламные блоки. Группы, состоящие из трёх наугад выбранных телезрителей, опрашивают относительно содержания рекламного блока. Рассчитать вероятности числа лиц в группе, которые смотрят рекламные блоки.
Решение:
Вероятность того, что наугад выбранный зритель данной телепрограммы смотрит и рекламные блоки, согласно статистическому определению вероятности, равна 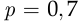 . Интерпретируя опрос трёх телезрителей как три испытания Бернулли и считая успехом ситуацию, когда телезритель смотрит рекламные блоки, найдём искомые вероятности по формуле Бернулли (2.10), в которой
. Интерпретируя опрос трёх телезрителей как три испытания Бернулли и считая успехом ситуацию, когда телезритель смотрит рекламные блоки, найдём искомые вероятности по формуле Бернулли (2.10), в которой
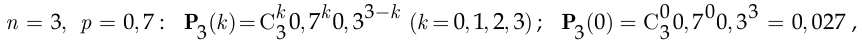
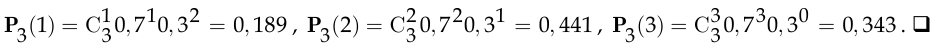
Курсовая работа №25
- В условиях предыдущей задачи найти наивероятнейшее число лиц в группе, которые смотрят рекламные блоки.
Решение:
Наивероятнейшее число 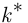 лиц в группе, которые смотрят рекламные блоки, подчиняется неравенствам (2.11):
лиц в группе, которые смотрят рекламные блоки, подчиняется неравенствам (2.11):
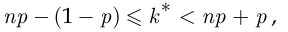
в которых
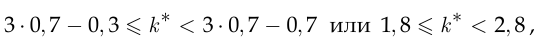
откуда
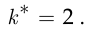
Это подтверждается и решением предыдущей задачи. □
Курсовая работа №26
- Из 1 000 опрошенных 700 человек поддерживают некоторую правительственную программу. Найти минимальную численность группы, в которой с вероятностью, не меньшей 0,9, хотя бы один респондент не поддерживает эту программу.
Решение:
Пусть численность группы равна 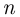 . Будем интерпретировать опрос группы из
. Будем интерпретировать опрос группы из 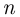 человек как испытания Бернулли, считая успехом то, что случайно выбранный респондент поддерживает правительственную программу. Согласно статистическому определению вероятности, вероятность успеха равна
человек как испытания Бернулли, считая успехом то, что случайно выбранный респондент поддерживает правительственную программу. Согласно статистическому определению вероятности, вероятность успеха равна
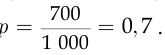
Пусть событие 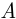 состоит в том, что в группе из
состоит в том, что в группе из 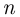 человек хотя бы один не поддерживает правительственную программу, тогда событие
человек хотя бы один не поддерживает правительственную программу, тогда событие 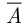 означает, что в группе из
означает, что в группе из 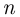 человек все
человек все 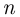 поддерживают эту программу.
поддерживают эту программу.
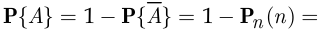
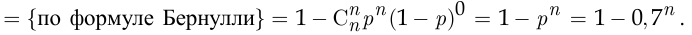
По условию вероятность 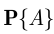 должна быть не меньше 0,9, поэтому 1
должна быть не меньше 0,9, поэтому 1
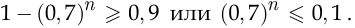
Чтобы найти минимальное значение 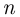 , при котором выполняется это неравенство, будем последовательно подставлять в него числа 1, 2, 3 и т.д., пока неравенство не удовлетворится:
, при котором выполняется это неравенство, будем последовательно подставлять в него числа 1, 2, 3 и т.д., пока неравенство не удовлетворится:
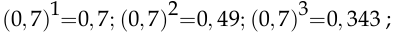
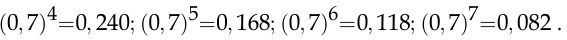
Видно, что неравенство 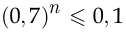 не выполняется при
не выполняется при 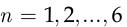 , но выполняется при
, но выполняется при 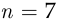 , поэтому минимальная численность группы, в которой с вероятностью, не меньшей 0,9, хотя бы один респондент не поддерживает эту программу, равна 7 чел. □
, поэтому минимальная численность группы, в которой с вероятностью, не меньшей 0,9, хотя бы один респондент не поддерживает эту программу, равна 7 чел. □
Курсовая работа №27
- Задача о разделе ставки. Петя и Маша часто играют в бильярд друг с другом, причём Петя выигрывает в два раза чаще, чем Маша. Исходя из этого, они оценили свои вероятности победить как
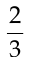 для Пети и
для Пети и 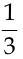 для Маши и начали турнир на следующих условиях: каждый выигрыш приносит одно очко, Петя для победы должен набрать двенадцать очков, а Маша — шесть. После того, как Петя набрал восемь очков, а Маша — четыре, игру пришлось прекратить, и победу решили присудить тому, у кого вероятность окончательного выигрыша больше. Определить, кому присудили победу в этом турнире.
для Маши и начали турнир на следующих условиях: каждый выигрыш приносит одно очко, Петя для победы должен набрать двенадцать очков, а Маша — шесть. После того, как Петя набрал восемь очков, а Маша — четыре, игру пришлось прекратить, и победу решили присудить тому, у кого вероятность окончательного выигрыша больше. Определить, кому присудили победу в этом турнире.
Решение:
Очевидно, максимальное количество партий, которое осталось сыграть Пете и Маше, равно пяти (либо Петя выиграет три раза, а Маша — два раза, либо Маша выиграет один раз, а Петя — четыре раза). Поэтому событие, заключающееся в выигрыше Пети (а значит, проигрыше Маши), состоит в том, что Маша из пяти партий не выиграет ни одной или выиграет всего одну. Поэтому вероятность выигрыша Пети равна вероятности того, что в пяти испытаниях Бернулли, в каждом из которых успех интерпретируется как выигрыш Машей очередной партии (т.е. вероятность успеха в каждом испытании составляет 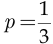 ), наступит 0 или 1 успех:
), наступит 0 или 1 успех:

Поэтому в данном случае победу должны были присудить Маше. □
Курсовая работа №28
- Задача Банаха. Известный математик Стефан Банах всегда носил с собой две коробки спичек, в каждой из которых первоначально было
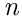 спичек. Каждый раз, когда он хотел зажечь спичку, Банах доставал наугад одну из коробок. Найти вероятность того, что когда он в первый раз вынимал пустую коробку, в другой коробке оказывалось ровно
спичек. Каждый раз, когда он хотел зажечь спичку, Банах доставал наугад одну из коробок. Найти вероятность того, что когда он в первый раз вынимал пустую коробку, в другой коробке оказывалось ровно 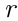 спичек, где
спичек, где 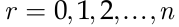 .
.
Решение:
Спички брались всего 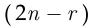 раз, причём
раз, причём 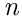 раз из коробки, оказавшейся пустой. Это соответствует
раз из коробки, оказавшейся пустой. Это соответствует 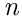 успехам в
успехам в 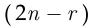 независимых испытаниях, поэтому вероятность
независимых испытаниях, поэтому вероятность 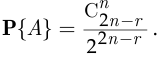
Курсовая работа №29
- На лекции по теории вероятностей присутствует 200 человек. Вероятность того, что день рождения случайно выбранного студента приходится на определённый день года, составляет
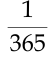 . Найти вероятность того, что один человек из присутствующих родился 1 января, и два человека родились 8 марта.
. Найти вероятность того, что один человек из присутствующих родился 1 января, и два человека родились 8 марта.
Решение:
Пусть событие 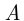 состоит в том, что случайно выбранный студент родился 1 января, событие
состоит в том, что случайно выбранный студент родился 1 января, событие 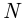 — в том, что
— в том, что 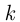 человек из 200 родились 1 января. Тогда по условию
человек из 200 родились 1 января. Тогда по условию
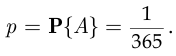
Предположим, что опрос 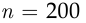 студентов относительно даты их рождения удовлетворяет условиям, которые накладываются на испытания Бернулли, где успехом единичного испытания считается наступление события
студентов относительно даты их рождения удовлетворяет условиям, которые накладываются на испытания Бернулли, где успехом единичного испытания считается наступление события 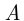 . Тогда, поскольку
. Тогда, поскольку 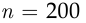 велико, а произведение
велико, а произведение
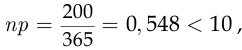
для подсчёта вероятности события 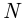 можно воспользоваться формулой Пуассона:
можно воспользоваться формулой Пуассона:
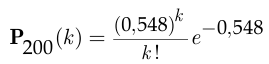
и при 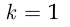 получаем
получаем
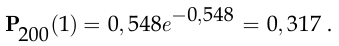
Пусть событие 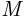 состоит в том, что
состоит в том, что 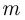 человек из 200 родились 8 марта. Тогда в соответствии с формулой умножения вероятностей,
человек из 200 родились 8 марта. Тогда в соответствии с формулой умножения вероятностей,
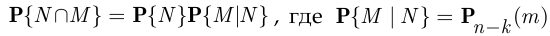
вероятность того, что из 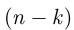 студентов га родились 8 марта. Так как число
студентов га родились 8 марта. Так как число
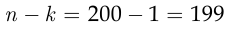
велико, а
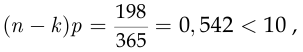
для расчёта вероятности события 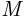 можно вновь воспользоваться формулой Пуассона:
можно вновь воспользоваться формулой Пуассона:
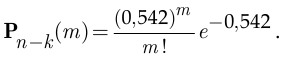
При
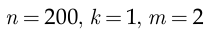
получаем:
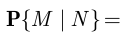
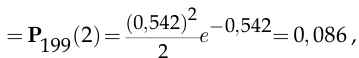
поэтому искомая вероятность
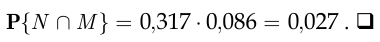
Возможно эти страницы вам будут полезны:
- Решение задач по теории вероятностей
- Помощь по теории вероятности
- Заказать работу по теории вероятности
- Контрольная работа по теории вероятности
- Решение задач по математической статистике
- Помощь по математической статистике
- Заказать работу по математической статистике
- Контрольная работа по математической статистике
- Курсовая работа по математической статистике
- Теория вероятностей краткий курс для школьников и студентов

