Оглавление:
Множество на плоскости (или в пространстве) называется ограниченным, если существует круг (или шар, если речь идет о пространстве), внутри которого целиком лежит это множество.
Точка называется граничной, если в любой окрестности этой точки найдутся точки как самого множества, так и его дополнения. Точка множества, которая не является граничной, называется внутренней. Множество всех граничных точек множества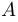 
называется его границей и обозначается через 
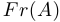. Граничная точка не обязана принадлежать самому множеству. Если ни одна из точек границы не принадлежит самому множеству, то такое множество называется открытым. Если, наоборот, все точки границы входят в само множество, то множество называется замкнутым.
Множество на плоскости (или в пространстве) называется выпуклым, если из того, что две точки принадлежат этому множеству, следует, что и отрезок, соединяющий эти точки, целиком содержится в этом множестве.
Мы будем рассматривать, как правило, множества, определяемые системами условий на координаты точек, выраженными в форме неравенств. На рисунке указаны три примера таких множеств.
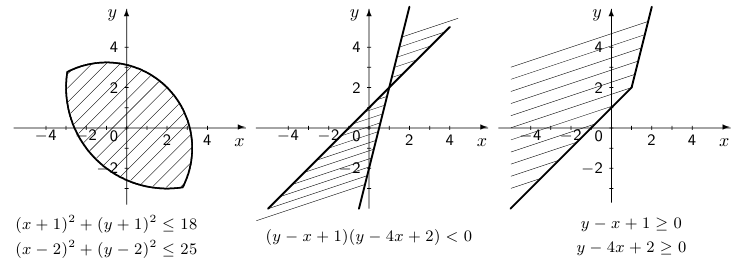
Упр. 1. Укажите, какие из множеств, заштрихованных на рисунке, являются выпуклыми. Изобразите множества, определяемые неравенствами противоположного направления. Какие из этих множеств являются ограниченными, а какие неограниченными?
Следующие понятия вводятся только для непрерывных функций, определенных на всей прямой или некотором промежутке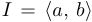 
, конечном или бесконечном.
Надграфиком функции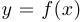 
называется множество точек на плоскости, первая координата которых принадлежит 
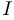, и которые лежат не ниже графика функции, то есть множество
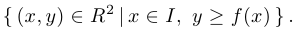
Соответственно определяется подграфик:
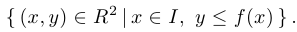
Функция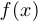 
называется выпуклой или выпуклой вниз, если ее надграфик — выпуклое множество, и вогнутой или выпуклой вверх, если ее подграфик является выпуклым.
Следующие определения для непрерывных функций эквивалентны вышеприведенным (попробуйте это доказать самостоятельно, хотя это упражнение уже потруднее):
Функция 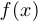называется вогнутой (выпуклой вверх) на каком-нибудь отрезке, если для любых двух точек 
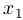и 
и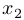з этого отрезка выполняется неравенство
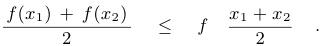
Если выполняется обратное неравенство, то функция называется выпуклой вниз или просто выпуклой. Если используемые в определении неравенства являются строгими при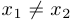 
, то соответствующие свойства называются строгими.
Пример 1.
Функция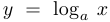 
при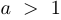 
является выпуклой вверх или вогнутой, а при 
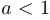— выпуклой вниз.
При этом неравенство обращается в равенство лишь в том случае, если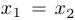 
, что означает, что функция строго вогнута.
Для непрерывной функции понятие вогнутости имеет простую геометрическую интерпретацию: хорда, соединяющая любые две точки графика, лежит ниже соответствующего участка графика (см. рисунок). Например:
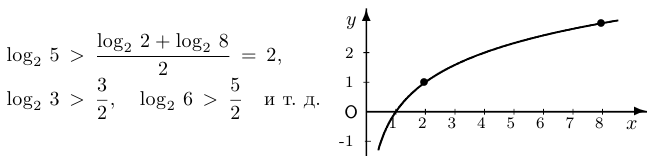
Опорные прямые па плоскости.
Прямая на плоскости называется опорной к множеству, если множество целиком содержится в одной из замкнутых полуплоскостей, на которые прямая делит всю плоскость и при этом имеет с прямой хотя бы одну общую точку.
Соответственно, плоскость в пространстве называется опорной, если множество целиком содержится в одном из замкнутых полупространств, на которые плоскость делит все пространство и при этом имеет с плоскостью хотя бы одну общую точку.
Естественно, что каждая точка множества, через которую проходит опорная прямая (или плоскость, если речь идет о множествах в пространстве), является граничной. Для выпуклых множеств верно и обратное — через каждую граничную точку проходит хотя бы одна опорная прямая (плоскость). (Заметим, что это свойство может служить другим, эквивалентным определением выпуклого множества.)
Если таких прямых (плоскостей) несколько, то точка называется угловой. Если же эта прямая или плоскость единственна, то она называется касательной в данной точке.
В случае, если речь идет о функциях, прямая рассматривается как опорная к надграфику или подграфику в зависимости от того, выпукла функция или вогнута.
Если опорная прямая в некоторой точке единственна, то она называется касательной в данной точке к графику функции. В этом случае говорят, что функция дифференцируема в данной точке, а тангенс угла наклона касательной к положительному направлению оси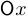 
называется производной функции в точке:
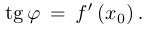
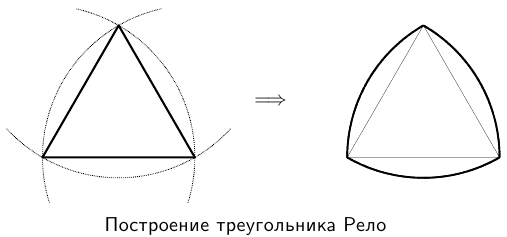
Треугольник Рело.
Если выпуклое множество на плоскости ограничено, то интуитивно понятно, что для каждой прямой на плоскости можно построить две параллельные ей опорные прямые такие, что множество целиком лежит между ними. Расстояние между такими опорными прямыми называется шириной множества в данном направлении. Если менять направление, то есть первоначальную прямую, то и ширина может меняться. Максимальное ее значение называется диаметром множества.
Множество, ширина которого не зависит от направления, называется множеством постоянной ширины. Очевидным примером такого множества является круг. Все остальные примеры менее тривиальны. Наиболее известным из них является треугольник Рело, который строится так, как показано на рисунке: он имеет три угловых точки, являющиеся вершинами равностороннего треугольника, и три криволинейных «стороны», которые являются дугами окружностей радиуса, равного стороне этого треугольника.
Экстремальное свойство треугольника Рело состоит в том, что это наименьшая по площади из выпуклых фигур постоянной ширины, внутри которых отрезок заданной длины можно развернуть на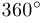 
. Интересно, что для более широкого класса фигур на плоскости, ограниченных замкнутой непрерывной кривой (не обязательно являющихся выпуклыми), указанная экстремальная задача не имеет решения в следующем смысле: для любого 
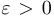можно построить фигуру, площадь которой будет меньше 
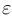, внутри которой можно осуществить разворот отрезка заданной длины на .
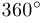Характерное свойство фигур постоянной ширины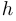 
состоит в том, что их периметр (длина границы) всегда равен одному и тому же числу, зависящему только от 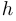, а именно 
.
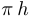На этой странице найдёте другие готовые курсовые работы во высшей математике:
Много готовых курсовых работ по высшей математике
Можете посмотреть другие готовые курсовые работы по высшей математике:
