Контрольные работы по финансовой математике

Готовые контрольные работы по финансовой математике с решением, и с подробное теорией для лучшего понимания.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Финансовая математика

Впервые финансовыми расчётами начали заниматься англичане (XVII — XVIII века). Ими занимались математики, физики и даже астрономы, словом, далёкие от финансов люди. Затем появились специалисты. Примерно в XVIII веке финансисты наткнулись на неразрешимые задачи. Например, требовалось найти корни алгебраических уравнений 7-й и 8-й степени с переменными коэффициентами. Поэтому XIX и XX век были веками провала финансовых расчётов, пока не появились ЭВМ — сначала на западе, а потом и у нас.

Возможно эта страница вам будет полезна:

Предмет финансовая математика

Рассмотрим простейшую кредитную операцию с участием всего лишь двух сторон: одна сторона — инвестор (даёт деньги), а вторая — заёмщик (берёт деньги).

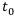— начало финансовой операции,

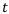— окончание финансовой операции,

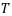— продолжительность финансовой операции,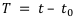

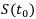— начальная денежная стоимость

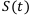— конечная денежная стоимость

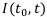— абсолютное приращение капитала

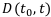— дисконт (скидка)

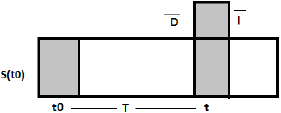
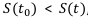, т.е. деньги всегда возвращаются в большем объёме, а вот на сколько больше — это и есть денежное приращение.

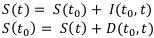
Т.е. численно приращение от дисконта ничем не отличается, однако используется в разных финансовых операциях.

Формула (0.1) выражает финансовую операцию наращение денег. Формула (0.2) выражает операцию дисконтирования (или учёта) денег. Формулы (0.1) и (0.2) являются основными формулами для денежных расчётов. Их недостаток заключается в том, что они выражают деньги, а с миллионами-миллиардами их использование становится неудобным.

Процентной ставкой называется отношение приращение капитала к начальной денежной сумме.

Формула процентной ставки:

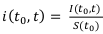
Учётной ставкой называется отношение дисконта к конченой денежной сумме.

Формула учётной ставки:

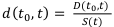
Перепишем формулы (0.1) и (0.2) через эти ставки:

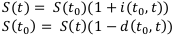
Эти формулы выражают безразмерную величину, поэтому их использование намного удобнее.

Коэффициентов наращение называется величина 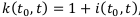по-другому его называют множителем наращения или мультиплицирующим множителем.

Коэффициентом дисконтирования называется величина .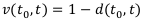

Перепишем формулы (0.1) и (0.2) через эти коэффициенты:

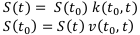
Основными базовыми периодами начисления или учёта денег считаются: год, полгода, квартал, месяц, неделя, день, час, минута, секунда. И самый маленький промежуток — мгновение. Это бесконечно малая, предел равен 0. Даже на таком периоде как мгновение происходит наращение денег. Но здесь уже нужно интегрировать.

Самым основным периодами является финансовый год. Длительность операции на данном периоде принимают за единицу.

Приращение является инвариантным, т.е. не имеет привязки по времени.

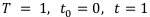
Если базовым промежутком является год, то приняты следующие сокращения:

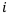— годовая процентная ставка,

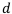— Годовая учётная ставка,

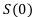— начальная денежная сумма,

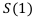— конечная денежная сумма через год.

С учётом этих сокращений формулы примут следующий вид:

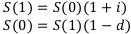
Эти формулы можно записать и так:

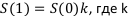— годовой коэффициент наращения

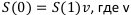— годовой коэффициент дисконтирования.

Таким образом, годовые коэффициенты наращения и дисконтирования —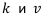— взаимообратным, если начальная и конечная денежная сумма неизменны: .

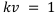Ставки, соответствующие равенству (0.11) называются эквивалентными.

Найдём эти ставки:

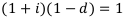
Выражения годовой процентной ставки через эквивалентную ей годовую учётную ставку: 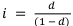. Выражение годовой учётной ставки через эквивалентную ей годовую процентную ставку: .

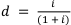Пусть учётная ставка 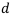= 50%, т.е. 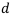= 0,5. Тогда соответствующая ей годовая процентная ставка равна 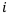= 100%. Т.е. положим 1000 рублей под 100% в банк, получим через год 2000.

Пусть процентная ставка 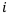= 25%, т.е. 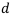= 0,25. Тогда соответствующая ей годовая учётная ставка равна d = 20%.

Пусть учётная ставка 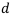= 10%, т.е. 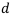= 0,1. Тогда соответствующая ей годовая процентная ставка равна 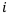= 11,11%.

По нашим примерам получается, что .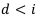

Это соотношение всегда верно.

Возможно эта страница вам будет полезна:

Помощь по финансовой математике

Финансовая арифметика

В этом разделе:

• Простые проценты
• Сложные проценты
• Непрерывные проценты

Простые проценты — это схема начисления или учёта денег, в которой приращение капитала на каждом периоде неизменно. Скажем, при 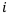= 20% и начальной сумме 1000 получаем следующие суммы через одинаковые периоды начисления: 1200 — 1400 — 1600 и т.д.

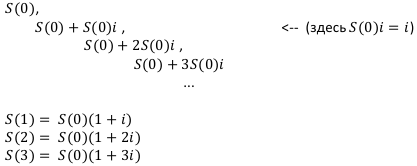
… и т. д.

Получаем формулу:

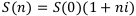
Формула (1.1) называется наращиваемой суммой по годовой ставке простых процентов за n лет.

Найдём стоимость этих денег на один год раньше, т.е. 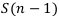из формулы :

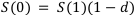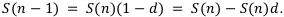
Теперь на два года раньше:

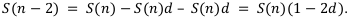
Тогда получаем следующую общую формулу:

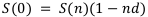
Формула (1.2) называется наращенной суммой, а обозначение 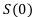в формуле (1.2) называется современной (т.е. текущей) суммой. Тут важно подчеркнуть, что n может быть любым, необязательно целым.

Ряд наращенных или дисконтированных денежных сумм представляет собой арифметическую прогрессию. Графиком наращения является прямая с положительным угловым коэффициентом.

Контрольная работа №1

Начальная сумма 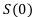= 500 т. р.

Процентная ставка 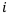= 20%

Найти: наращенную сумму через 2,5 года: 5(2,5).

Решение:

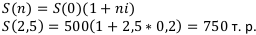
Это операция наращения, поэтому дисконта здесь нет, а есть приращение капитала: 750 — 500 = 250.

Контрольная работа №2

Вексель номиналом 700 т. р. и сроком погашения 31 декабря 2012 года учитывается сегодня (2 февраля 2012 года) по годовой учётной ставке d = 20%. Какую сумму получит держатель векселя?

Решение:

Номинал векселя — это конечная сумма, а не начальная, т.е. 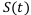= 700 т. р. Тогда t = 31.12.2012. А сегодня 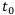= 2.2.2012. Нужно найти современную стоимость, т.е. сколько стоят эти деньги сейчас. Это операция дисконтирования или учёта. Вектор этой операции противоположен вектору операции наращения.

Найдём срок: 31 декабря 2012 — 2 февраля 2012 равно 333 дня. Т = 333 дней. Но нам надо выразить всё в годах: 333 / 366 = 0,9098 года. Для нашей формулы это п = 0,9098

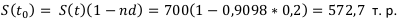
Итого: .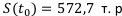

Контрольная работа №3

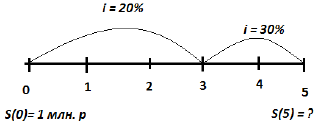
Решение:

Посчитаем коэффициенты наращения k:

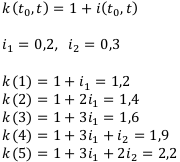
Ответ: .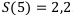

Переменные ставки простых процентов

Исходя из предыдущего примера, выделим общую формулу для подсчёта коэффициента начисления при переменной ставке.

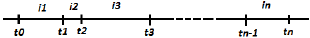
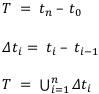
Коэффициент наращения по переменным ставкам простых процентов имеет вид:

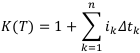
Сложные проценты

В сложных процентах при 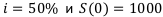деньги будут расти по следующей последовательности: 1000 — 1500 — 2250 — 3375 — 5062. Т.е. каждая следующая сумма в полтора раза больше предыдущей.

Схема сложных процентов предполагает, что коэффициент наращения или дисконтирования на всём промежутке начисления или учёта процентов остаётся неизменным.

Ряд наращенных сумм по сложным процентам представляет собой геометрическую прогрессию. Графиком наращения или дисконтирования является экспонента, или, по-другому, показательная функция.

Выведем формулы.

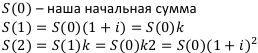
В общем виде наращенная сумма по сложным процентам равна:

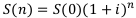
Теперь выведем формулу дисконтирования.

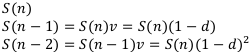
За n шагов добираемся до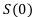

В общем виде современная стоимость денег по сложным процентам равна:

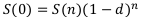
Решим примеры 1 и 2 по сложным процентам.

Возможно эта страница вам будет полезна:

Примеры решения задач по финансовой математике

Контрольная работа №4

Начальная сумма 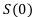= 500 т. р.

Процентная ставка 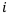= 20%

Найти: наращенную сумму через 2,5 года: .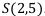

Решение:

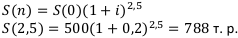
Контрольная работа №5

Вексель номиналом 700 т. р. и сроком погашения 31 декабря 2012 года учитывается сегодня (2 февраля 2012 года) по годовой учётной ставке 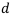= 20%. Какую сумму получит держатель векселя?

Решение:

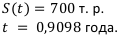
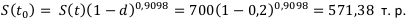
Сравнительный анализ простых и сложных процентов

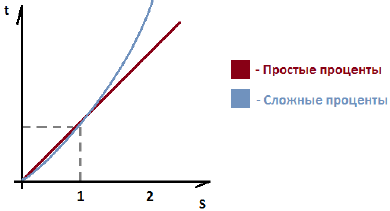
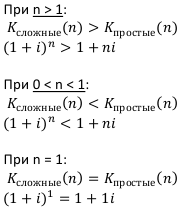
Где К — коэффициент наращения.

Эти неравенства очень просто доказываются, достаточно подставить в формулы, например, 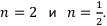Таким образом, если срок наращения денег меньше года, то в сложных процентах деньги наращиваются медленнее, чем в простых. Если же срок равен единице, т.е. году, то разницы нет. Если же срок выше одного года, то в сложных процентах деньги наращиваются быстрее, чем в простых. Аналогично дела обстоят с дисконтированием.

Чтобы доказать неравенства в общем виде, нужно использовать формулу Тейлора:

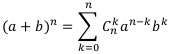
где 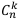— это число сочетаний .

Тогда:

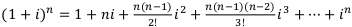
Получаем:

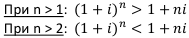
Запишем вывод с точки зрения инвестора:

если договор краткосрочный, т. е. сроком меньше года, то для инвестора более выгодны простые проценты. Если договор долгосрочный, т. е. сроком больше года, то для инвестора более выгодны сложные проценты.

Для заёмщика — всё наоборот.

Номинальные ставки

Обозначим через 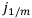процентную ставку, действующую на 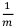-ой части года .

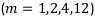Годовой номинальной процентной ставкой называется величина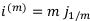

Т.е. проценты начисляются не раз в год, a m раз в год.

Пример: если 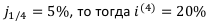. Т. е. годовая ставка равна 20%, однако проценты начисляются 4 раза в год (ежеквартально) по 5%.

Рассчитаем коэффициент наращения по простым процентам:

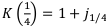
Номинальные ставки по простым процентам рассматривать не имеет смысла — хоть проценты начисляются и несколько раз в год, эффект от них будет одним и тем же. А вот по сложным процентам эффект есть.

Коэффициенты наращения по сложным процентам:

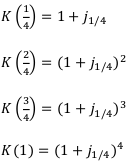
Исходя из этого, выведем общую формулу. Коэффициент наращения по годовой номинальной процентной ставке 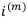за n лет равен:

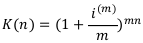
Пусть 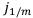— учётная ставка, действующая на 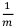-ой части года. Запишем определение годовой номинальной учётной ставки по аналогии.

Годовой номинальной учётной ставкой называется величина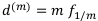

Пусть 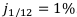Тогда соответствующая годовая учётная ставка равна .

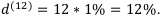Пусть учёт происходит на периоде один год: коэффициент дисконтирования за один квартал равен 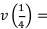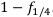Если же учет производится за два квартала, то никакого смысла учёта по простым процентам нет. А вот по сложным процентам было бы уже так:

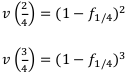
Запишем общую формулу.

Коэффициент дисконтирования по годовой номинальной учётной ставке за n лет равен:

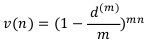
Выведем формулы будущей и современной суммы денег:

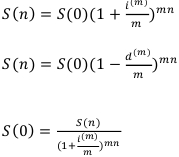
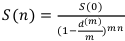
Учёт денег по формуле (6) называется банковским учётом, а по формуле (7) — математическим учётом. На практике формулы (7) и (8) используются редко.

Ставка называется эффективной, если она эквивалентна по силе наращения или учёта соответствующей номинальной ставке.

Уравнение эквивалентности между эффективными и номинальными процентными ставками имеет вид:

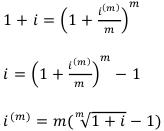
Формула (10) показывает соотношение между годовой эффективной и годовой номинальной процентной ставкой.

Выражение эквивалентности между годовой эффективной и годовой номинальной учётной ставкой имеет вид:

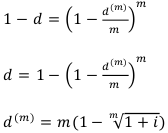
Пример:

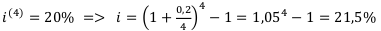
Пример 2:

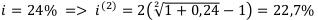
Пример 3:

Пусть дана учётная ставка 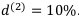. Нужно найти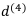

Составим уравнение эквивалентности с помощью коэффициентов дисконтирования:

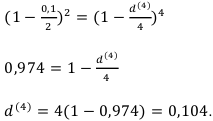
Всё.

Составим новое уравнение эквивалентности и выведем новые формулы:

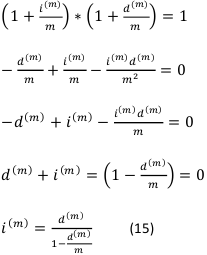
Это формула выражения годовой номинальной ставки через эквивалентную ей годовую учётную ставку.

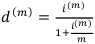
Это формула выражения годовой учётной ставки через эквивалентную ей годовую номинальную ставку.

Пример 4:

Пусть дана 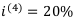. Найти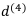

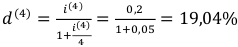
Ответ: 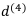= 19,04%.

Пример 5:

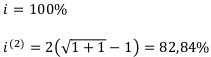
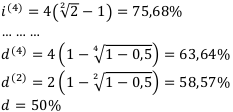
Ставки монотонно убывают.

Приходим к выводу, что эквивалентные номинальные и учётные ставки расположены в следующем порядке:

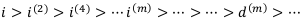
Т. е.:

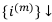— последовательность номинальной процентной ставки монотонно убывает

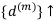— последовательность учётной процентной ставки монотонно возрастает.

Вопрос: имеют ли эти последовательности общий предел? Возьмём предел от формулы (16):

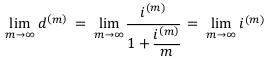
Из этого предельного равенства следует, что последовательности номинальных процентных и учётных ставок имеют общий предел. Этот предел обозначается буквой 8 и называется он силой процента или силой роста.

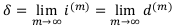
Запись 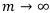означает, что число отрезков периода бесконечно увеличивается, т.е. начисление денег происходит ежесекундно, каждое мгновение.

Пример:

Как видим, сумма растёт совсем небыстро. Это число стремится к числу 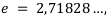т. е. на определённом этапе происходит стабилизация наращения суммы. Т. е. если мы будем производить начисление каждое мгновение, то приращение суммы не превысит число 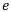. При ежемгновенном начислении процентов при эффективной ставке 100% первоначальный капитал за год увеличивается в 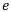раз.

Выведем формулы для коэффициентов дисконтирования и соответствующие им денежные стоимости.

Рассмотрим годовой коэффициент наращения 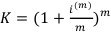по годовой номинальной процентной ставке m.

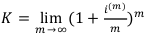
Вычислим этот предел с помощью второго замечательного предела:

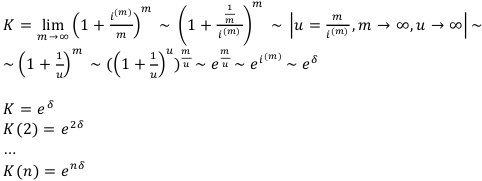
Теперь аналогично вычислим годовой коэффициент дисконтирования:

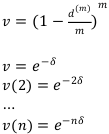
Расчётные формулы для наращенных и дисконтированных денежных стоимостей по непрерывным процентам:

Будущая стоимость денег по непрерывным процентам:

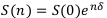
Современная стоимость денег по непрерывным процентам:

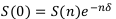
Пример:

найти период удвоения капитала.

Удвоение капитала означает, что коэффициент наращения равен 2: .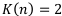

Рассмотрим три случая: по простым процентам, по сложным и непрерывным процентам.

Чем больше ставка, тем короче период удвоения. Например, если ставка равна 0%, то периодом удвоения будет бесконечность.

Предположим, ставка равна 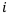= 20%.

1-й случай.

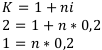
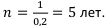
2-й случай — сложные проценты.

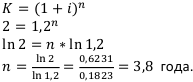
3-й случай — непрерывные проценты.

Получаем тот же ответ, что и во втором случае.

Так обстоят дела, если ставка постоянна.

Переменные ставки сложных процентов

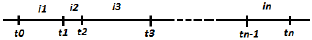
Весь период начисления разбит на временные интервалы. На каждом интервале действует своя ставка.

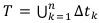
Вычислим коэффициент наращения:

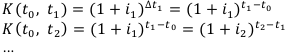
В общем случае коэффициент наращения по переменным ставкам сложных процентов на всём промежутке начисления процентов равен:

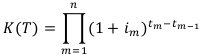
Контрольная работа №6

Договор предусматривает начисление сложных процентов по следующей схеме: 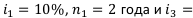40%, 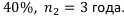. Найти коэффициент наращения за весь период начисления — 5 лет, т. е. — ?

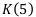Решение:

Построим график:

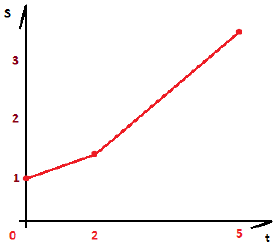
Рассмотрим случай, когда сила процента является переменной и представлена функцией: .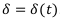

В теории финансовой математики рассматривают функции только следующих типов:

• кусочно-постоянные
• линейные
• кусочно-линейные
• квадратичные

Рассмотрим первый случай.

Пусть 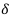задан следующим образом:

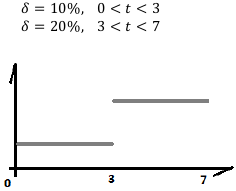
Найдём коэффициент наращения на всём периоде.

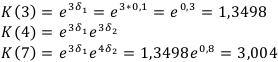
Рассмотрим второй случай: 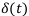— линейная функция.

Пусть 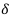задан следующим образом:

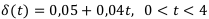
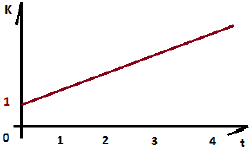
Вычислить коэффициент наращения за 4 года: К(4) — ?

Так как коэффициент приращения непостоянен, нужно вывести для него формулу.

Для решения этой задачи выведем формулу для коэффициентов наращения и дисконтирования по переменной силе процента. Пусть 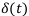— это произвольная кривая.

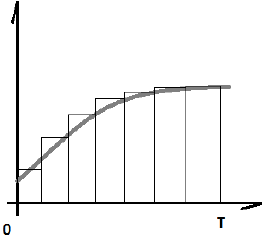
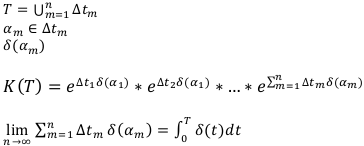
Таким образом, коэффициент наращения по переменной силе процента на периоде Т равен:

Коэффициент дисконтирования по переменной силе процента на периоде Т равен:

Возвращаясь к примеру, находим наш коэффициент наращения:

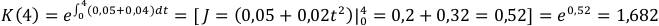
В случае кусочно-линейной функции — ломаной — нужно взять интеграл на каждом линейном кусочке и перемножить их.

В субботу 11-го февраля — контрольная работа.

Контрольная работа №7

некто купил магазин за 10 миллионов, а через пять лет — продал за 20 миллионов. Найти доходность этой финансовой операции.

Решение:

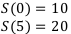
Доходность — это не разница между суммой покупки и суммой продажи. Как и все остальные величины, доходность — величина относительная и чаще всего выражается в ставках. Найдём доходность через годовую процентную ставку. А для этого нужно записать уравнение эквивалентности.

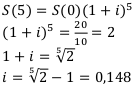
Ответ: доходность данной операции равна 0,148.

Контрольная работа №8

По условиям контракта должник уплачивает 36 тысяч рублей через 100 дней. Кредит предоставлен под годовую процентную ставку 14%. Определить величину кредита и сумму дисконта, если для дисконтирования погашаемого долга используется математический учёт простыми процентами.

Дано:

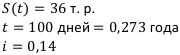
Найти: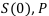

Решение:

Найдём начальную сумму:

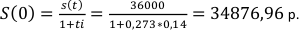
Дисконт:

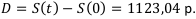
Контрольная работа №9

Определить срок долга, который необходим для того чтобы первоначальный долг в 20 000 тысяч рублей вырос до величины 30 000 рублей при условии, что на сумму долга начисляются простые проценты при годовой учётной ставке 11%.

Решение:

Дано:

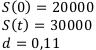
Найти: t

Запишем уравнение эквивалентности через учётную ставку — 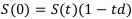— и выразим из него t:

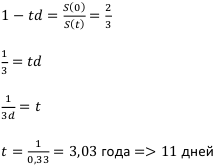
Контрольная работа №10

Определить величину дисконта при продаже финансового инструмента на сумму 5 000 долларов, если до срока погашения осталось 2,5 года. Банк, покупающий этот инструмент, применяет сложные проценты по годовой учётной ставке 9 процентов.

Решение:

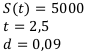
Найти: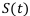

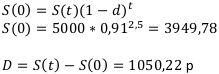
Контрольная работа №11

Определить силу процента за 4 года, если начальная сумма составляла 100 000 рублей, а конечная — 160 000 рублей.

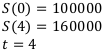
Найти: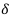

Решение:

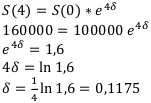
Контрольная работа №12

Инвестиционная компания купила склад за 6 млн. рублей, а спустя 5 лет — продала за 10 млн. лет. Определить доходность финансовой операции в виде силы процента.

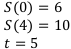
Найти: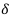

Решение:

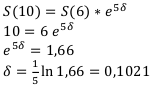
Контрольная работа №13

Два года назад фирма купила машину за 6000. Современная оценка этой машины составила 4500 долларов. Предполагая, что стоимость машины амортизируется по экспоненте, определить стоимость машины через 3 года.

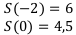
Найти: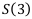

Решение:

раз стоимость машины амортизируется по экспоненте, значит, её стоимость растёт по сложным и непрерывным процентам. Будем использовать процентную ставку. Составим уравнение эквивалентности:

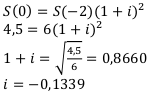
Это так называемая ставка амортизации

Найдём стоимость через 3 года:

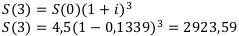
Стоимость машины уменьшается экспоненциально:

Контрольная работа №14

Две фирмы имеют годовые обороты соответственно в 1 млн. рублей и 2 млн. рублей. Оборот первой фирмы ежемесячно растёт на 2%, а оборот второй — уменьшается на 1%. Через какой срок обороты фирм сравняются?

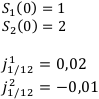
Найти: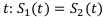

Решение:

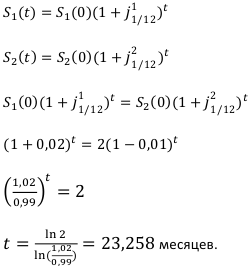
Возможно эта страница вам будет полезна:

Курсовая работа по финансовой математике

Финансовая рента

Финансовая рента (аннуитет) — это поток платежей такой, что равные выплаты производятся через равные промежутки времени. Ренты бывают безусловные и условные. Рента называется безусловной, если известен общий срок ренты (выплата стипендии в течение срока обучения). Рента называется условной, если общий срок ренты заранее неизвестные или зависит от выполнения некоторого условия (например, страховые ли пенсионные выплаты). Условные ренты обычно рассматриваются в актуарной математике. Различают также ренты пренумерандо и постнумерандо.

Рента называется пренумерандо, если периодические выплаты производятся в начале каждого периода, и постнумерандо — если в конце каждого периода. Рента называется вечной, если её общий срок неограниченно большой.

Введём обозначения:

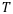— общий срок ренты

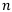— количество периодов ренты

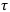— длительность одного периода

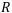— член ренты или периодическая выплата

Основными расчётными (денежными) характеристиками ренты являются:

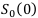— современная стоимость ренты пренумерандо

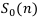— наращенная стоимость ренты пренумерандо

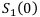— современная стоимость ренты постнумерандо

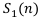— наращенная стоимость ренты постнумерандо

Графическое изображение ренты пренумерандо и постнумерандо:

Пренумерандо

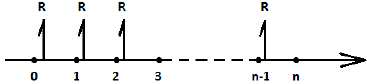
Постнумерандо

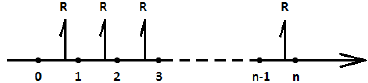
Будем считать сначала, что рента простая, т. е. начисление или учёт процентов, а также выплаты производятся один раз в году. Будем считать далее, что на рынке действуют следующе эквивалентные между собой ставки:

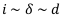
Вычислим величину 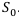. Используя формулу суммы геометрической прогрессии а также равенство 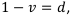получаем:

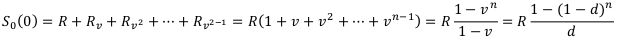
Далее вычислим величину 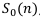, зная, что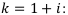

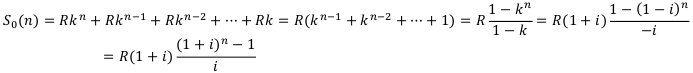
Аналогично находим величины 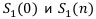относительно ренты постнумерандо. Окончательно получаем следующие расчётные формулы для простых рент пренумерандо и постнумерандо:

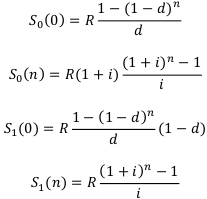
Любая сумма постнумерандо конечно меньше, чем пренумерандо. Чем дальше выплаты — тем дешевле стоят выплачиваемые деньги (дело не в инфляции, это просто свойство денег).

Вспомним кое-какие уравнения:

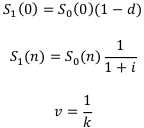
Финансовая рента часто используется в задачах погашения кредита.

Контрольная работа №15

Кредит в размере 300 000 рублей выплачивается ежегодно по годовой учётной ставке 20% в течение 3-х лет. Найти величину ежегодных выплат.

Решение:

Будем считать, что обслуживание кредита осуществляется по схеме постнумерандо.

Обозначения:

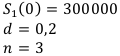
Найти:R

Решение:

Первоначальный кредит делим на коэффициент дисконтирования. Это формула (3.3).

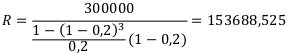
Это означает, что современная или наращенная стоимость ренты пренумерандо больше соответствующей стоимости ренты постнумерандо. Безразмерные величины в формула (3.1) — (3.4) — это коэффициенты ренты.

Коэффициент дисконтирования ренты пренумерандо:

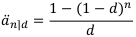
Коэффициент наращения ренты пренумерандо:

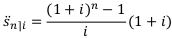
Коэффициент дисконтирования ренты постнумерандо:

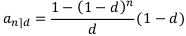
Коэффициент наращения ренты постнумерандо:

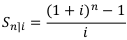
Таким образом получаем, что:

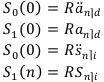
Сложная или (m,p)-pehta

Простая рента предполагала одно начисление или один учёт на одном периоде ренты и одну выплату на этом периоде. Пусть теперь на одном периоде производится …

Вспомним коэффициенты:

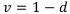— годовой коэффициент дисконтирования по годовой эффективной учётной ставке.

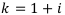— годовой коэффициент наращения по годовой эффективной процентной ставке.

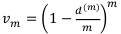— годовой коэффициент дисконтирования по годовой номинальной процентной ставке с m учётами в году.

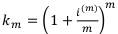— годовой коэффициент наращения по годовой номинальной процентной ставке с m начислениями в году.

Теперь представим, что у мы имеем р выплат в год. Тогда:

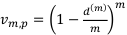— годовой коэффициент дисконтирования по годовой номинальной процентной ставке с m учётами в году на 1/р части года.

к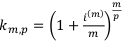 — годовой коэффициент наращения по годовой номинальной процентной ставке с m начислениями на 1/р части года.

На каждом частичном периоде выплата равна 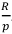. Однако величины 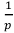в этой выплате обычно учитывают в коэффициентах ренты. Тогда:

v

Очевидно, что коэффициент дисконтирования сложной ренты постнумерандо меньше коэффициента сложной ренты пренумерандо. Точнее, он равен:

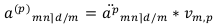
или:

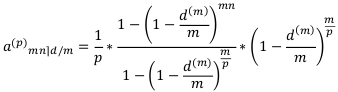
По аналогии коэффициент наращения сложной ренты пренумерандо равен:

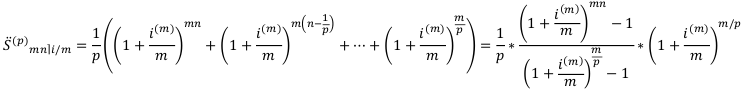
Коэффициент наращения сложной ренты постнумерандо равен:

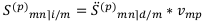
или:

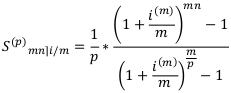
Итак, основные расчётные формулы для коэффициентов дисконтирования и наращения сложной ренты пренумерандо и постнумерандо имеют вид:

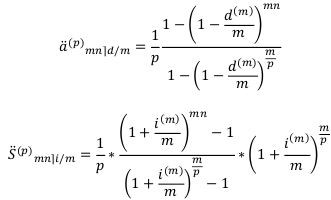
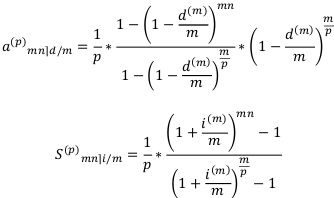
С помощью этих формул легко записать основные расчётные формулы для современных и наращенных стоимостей сложной ренты-пренумерандо и постнумерандо:

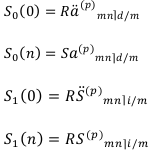
Рассмотрим несколько типичных случаев сложной ренты:

1. 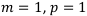, т. е. и выплаты производятся один раз в год, и начисление — один раз в год. Таким образом, сложная рента превращается в простую, и все коэффициенты сложной ренты сводятся к соответствующим коэффициентам для простой ренты.

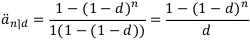
Аналогично и с остальными коэффициентами.

2. 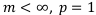, т. е. выплата производится один раз в год, а начислений или учётов — сколько угодно. Тогда подставив вместо р единицу, получим упрощённые формулы коэффициентов сложной ставки. Формулы станут менее громоздкими:

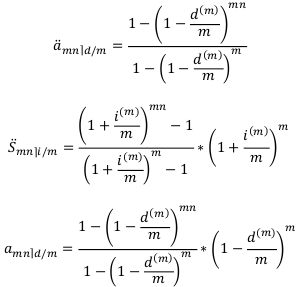
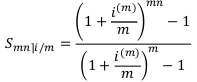
3. 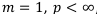, т. e. начисление или учёт производится раз в году, а выплаты — постоянно, например, ежемесячно. Тогда подставим в формулы коэффициентов единицу вместо m и снова сократим формулы. Буква «m» исчезнет даже из обозначений: 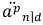и пр.

4. m = р, выплат производится столько же, сколько начислений или учётов. Этот случай похож на простую ренту, только вместо одного года надо брать -ю часть года. Но при этом ставка берётся уже не годовая. Вместо неё берутся 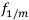для учёта и 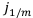для наращения.

5. 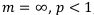, т. е. начисление идёт непрерывно, а выплата — дискретна. Переходим к пределам по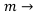 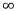и используем второй замечательный предел. Получим:

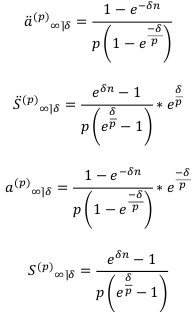
Возможно эта страница вам будет полезна:

Заказать работу по финансовой математике

Контрольная работа №16

Для создания страхового фонда ежегодно выделяется 4000 долларов. На аккумулируемые средства начисляются сложные проценты по ставке 6% годовых. Определить размер страхового фонда через 5 лет.

Общая модель — простая рента. Рента бывает пренумерандо и постнумерандо. Т. к. в задаче не уточняется, следует рассмотреть оба случая. Также ничего не сказано о ставке — процентная она или учётная. Следовательно, здесь также имеется 2 случая. Итого мы имеем 4 случая.

Решение:

1) Рента пренумерандо, процентная ставка.

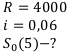
Используем Формулу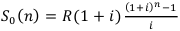

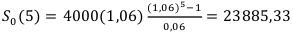
2) Рента постнумерандо, процентная ставка.

R = 4000

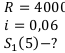
Используем Формулу —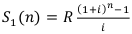

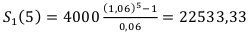
3) Рента пренумерандо, учётная ставка.

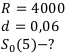
Переведём процентную ставку в учётную:

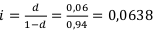
4) Рента постнумерандо, учётная ставка.

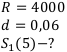
Переведём процентную ставку в учётную:

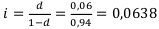
Используем Формулу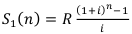

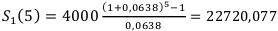
Контрольная работа №17

Нефтяная компания ежемесячно выплачивает пенсию $500. Предполагая, что годовая номинальная процентная ставка равна 12%, подсчитать современную величину пенсионных выплат.

Решение:

Т. к. пенсия выплачивается в начале месяца, это пренумерандо.

Нам нужно найти годовую учётную ставку. Переведём годовую номинальную процентную ставку в эффективную годовую процентную ставку, а её уже переведём в d.

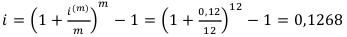
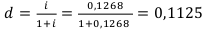
Теперь находим 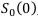, не забывая, что $500 — это ежемесячная пенсия, а мы ищем годовую сумму. Т. е. умножаем 500 на 12. Т. е. R = 6000

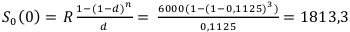
Контрольная работа №18

Молодожёны имеют годовой доход 8 $16000. Ипотечный банк выдаёт сумму, которая должна погашаться 1/3-ей месячного дохода. Банк использует сложные проценты по месячной процентной ставке 1,2%. Долг погашается в течение 25 лет. Какова величина взятого кредита?

Решение:

Выплаты кредита производятся обычно в конце месяца, поэтому мы имеем ренту постнумерандо.

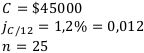
Найти: — ?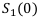

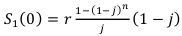
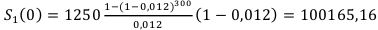— величина взятого кредита

А номинальная сумма, которую молодожёны выплатят в итоге, получается: 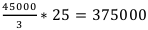. Т. е. больше чем в 3 раза превышает сумму кредита. Довольно жёсткие условия, но молодожёны согласились.

Контрольная работа №19

Накопительный фонд формируется по следующим схемам:

1. Годовая номинальная процентная ставка с ежеквартальным начислением процентов равна 12%, т. е.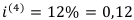

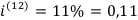
Сумма -1 миллион.

Вопрос: какая схема выгоднее?

Решение:

нужно сравнить коэффициенты наращения. Наиболее выгодной будет та схема, у которой он будет больше.

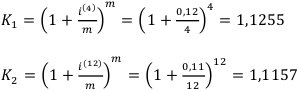
Вывод: вторая схема выгоднее.

Контрольная работа №20

Семья планирует купить автомобиль за $20000. Банк выдаёт кредит на 5 лет при следующих условиях: начисление процентов ежеквартально, а выплата денег производится ежемесячно. Годовая номинальная процентная ставка составляет 16%, т. е. 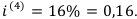. Найти величину ежемесячных выплат.

Решение:

Выплаты производятся в конце месяца, значит — рента постнумерандо

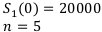
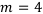— ежеквартальное начисление процентов

— количество выплат в году (ежемесячно)

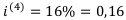
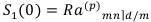
Вычислим d: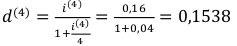

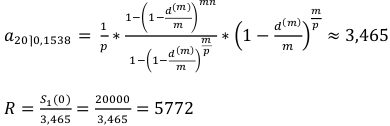
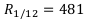доллар выплачиваем ежемесячно за этот кредит.

Подсчитаем номинальную сумму, которую мы вернём за такой кредит: 5772 * 5 = 28860. Переплата большая.

Анализ инвестиций

Анализ инвестиционных проектов проводится по многим экономическим и финансовым показателям, среди которых основными являются:

• Чистый дисконтированный доход (ЧДД или NPV)
• Внутренняя норма доходности (ВНД или IRR)
• Срок окупаемости (СО или IR)

Чистый дисконтированный доход — это суммарная стоимость всех дисконтированных платежей проекта:

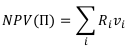
где 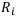— платежи в определённые моменты времени, причём 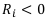, если это инвестиции, и 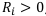, если это доход; 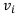— соответствующие дисконтные множители при известной ставке процентов. Чистый дисконтированный доход проекта называют также чистой приведённой стоимостью (NPV).

Уравнением безубыточности для проекта П называются уравнение следующего вида:

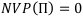
Корень ищется в действительной области. Степень уравнения очень велика, поэтому обычно решение ищется приближённо. Если инвестиционный проект верный, такой корень существует.

Известно, что если кумулятивный ряд платежей монотонно возрастает, то существует положительный корень этого уравнения. Ставка, советующая такому корню уравнения 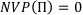, называется внутренней нормой доходности.

Срок окупаемости — это период, начиная с которого, доходная часть проекта превосходит расходную. Его можно рассчитать, используя кумулятивный ряд дисконтирования платежей. А именно тот момент, начиная с которого значения этого кумулятивного ряда становятся положительными, и указывает срок окупаемости проекта.

Контрольная работа №21

Надо сравнить два проекта и выбрать наилучший.

Провести сравнительный анализ двух проектов и выбрать наилучший по следующим параметрам: чистый дисконтированный доход, внутренняя норма доходности, срок окупаемости. Средневыборочная процентная ставка — 25%.

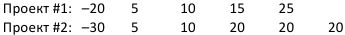
Решение:

по условию 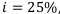, значит, коэффициент дисконтирования равен: 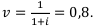. Подсчитаем чистую приведённую стоимость обоих проектов.

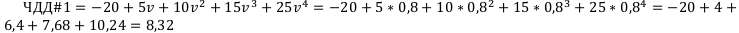
За счёт дисконтирования реальная стоимость проекта оказывается намного ниже номинальной.

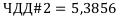
У второго проекта реальная стоимость ещё ниже.

Теперь подсчитаем внутреннюю норму доходности данных проектов. Для этого сначала составим уравнение безубыточности для первого проекта:

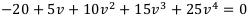
После упрощения уравнение примет вид:

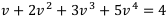
С помощью таблицы Excel легко находим 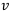= 0,706. Отсюда получаем: .

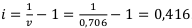Итак, внутренняя доходность первого проекта равна: 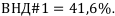. Аналогично составляем уравнение избыточности второго проекта и находим внутреннюю доходность второго проекта: .

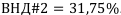Теперь, чтобы найти срок окупаемости, составим следующую таблицу:

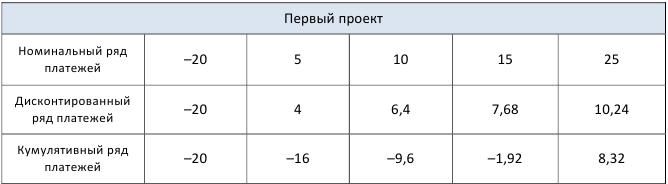
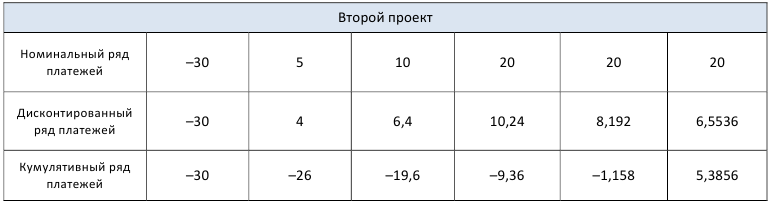
Из таблицы видим, что реальный срок окупаемости проекта №1 находится между 3-им 4-ым годами, т. к. на

концах этого отрезка значения кумулятивного ряда имеют противоположные знаки.

Воспользуемся формулой для уточнения сроков окупаемости первого и второго проекта:

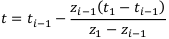
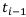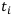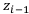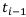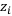где — левый конец отрезка, — правый; — значение кумулятивного ряда в точке — а значение ряда в точке 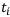. Левым концом отрезка считается тот год, на котором знак кумулятивного ряда сменяется.

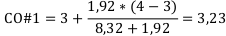
Т. е. срок окупаемости первого проекта составляет 3 года и 3 месяца.

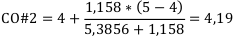
Т. е. срок окупаемости второго проекта составляет 4 года и 2 месяца.

Представим полученные результаты в виде таблицы:

Очевидно, что по всем показателям первый проект оказался более привлекательным, чем второй. Однако часто происходят ситуации, когда показатели неоднозначны. Поэтому для выбора проекта существуют некоторые рекомендации.

Оптимальное множество парето

Рассмотрим две финансовые операции:

где 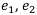— это доходы, а 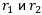— риски.

Тогда финансовая операция 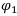доминирует операцию 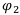, если 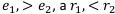(записывается как ).

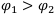Рассмотрим 6 финансовых операций:

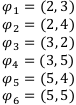
Проанализируем их по доходности и рискам и выясним их отношения доминирования:

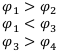
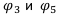не находятся в отношениях доминирования (у 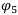больше доходность, но у 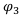меньше риски, поэтому ни одна из них не доминирует друг над другом)

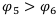
Те операции, которые лучше или хуже друг друга, вычёркиваем, оставляем только те, которые не доминируют друг над другом. В нашем случае это операци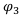и и 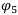. Эти две оставшиеся операции и будут составлять оптимальное множество Парето. Изобразим его графически:

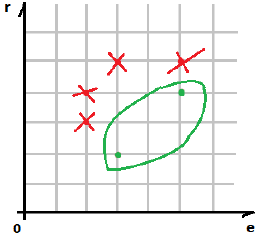
Таблица вывода формул

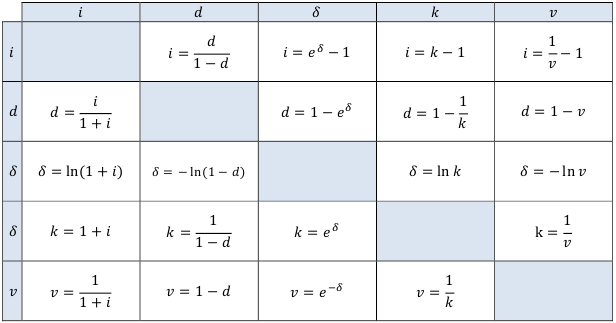
Любая финансовая операция протекает в условиях неопределённости, следовательно, денежные суммы также определены с некоторой вероятностью.

Под полной неопределённость будем понимать полное отсутствие всякой информации о финансовой операции. Под частичной неопределённостью понимаем знание о вероятностях исходов финансовой операции.

Финансовые операции и их исходы, выраженные некоторыми величинами удобно представлять в виде матрицы. В качестве таких величин (элементов матрицы) могут выступать доходы, эффективность, риски.

Рассмотрим матрицу доходов:

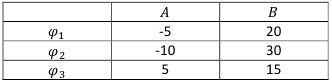
Нетрудно увидеть, что финансовая операция 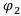более рискованна, чем операция 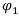Операция 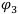при любых исходах А или В имеет положительный доход, но её также следует считать рискованной. В самом деле, если случится исход А, а не исход В, то относительно операции 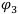возникает риск недобрать 10 = 15 — 5 денежных единиц.

В общем случае матрицу доходов будем обозначать Q.

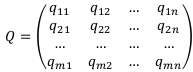
В этой матрице m строк, соответствующих m финансовым операциям, и n столбцов, соответствующих n исходам. Элемент 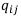такой матрицы — это доход от i-той финансовой операции при j-том исходе. Матрицу доходов называют также матрицей возможных решений, матрицей возможных последствий, матрицей эффективностей.

Другим важным параметром любой финансовой операции является риск. В простейшем случае матрица рисков R строится по известной матрице доходов Q:

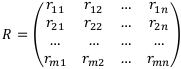
Очевидно, что матрицы Q и R одного размера, а именно, mxn. Каждый элемент матрицы R выражает риск некоторой финансовой операции при некотором исходе. Существует несколько измерителей риска. В простейшем случае риск 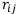можно вычислить по следующей формуле:

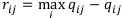
Здесь 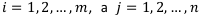. Из этой формулы следует, что для формирования матрицы рисков необходимо в каждом столбце найти наибольший элемент и из него вычесть все элементы этого столбца. Тогда число 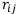может выражать, например, денежную сумму, недостающую до максимальной суммы в случае неудачного выбора финансовой операции при определённом исходе.

Одной из важнейших задач является задача выбора наилучшей финансовой операции из m операций, протекающих в условиях полной или частичной неопределённости исходов. В некоторых случаях наилучшая финансовая операция легко проглядывается по матрицам Q или R, однако более надёжный результат по выбору наилучшей операции можно достичь с применением математических методов.

Выбор наилучшей финансовой операции в условиях полной неопределённости

Эти методы базируются на теории игр.

В финансовой практике обычно применяют следующие решающие правила:

1. Правило Вальда (максиминное)
2. Правило Сэвиджа (минимаксное)
3. Правило Гурвица (взвешенное или оптимальное)

По правилу Вальда в каждой строке матриц доходов Q сначала выбирается минимальный элемент:

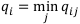
Затем из выбранных минимальных элементов находится максимальный:

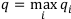
Соответствующая этому элементу финансовая операция объявляется наилучшей. Итак, оптимальный элемент, выбранный по этому правилу, равен:

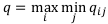
Исходя из финансового смысла выбора наилучшей финансовой операции по правилу Вальда, его можно назвать правилом крайнего пессимизма (правилом осторожного финансиста), потому что мы ориентируемся на самый неблагоприятный исход. Таким образом, q — это гарантированный доход финансиста, если он действует по этому правилу.

По правилу Сэвиджа в каждой строке матрицы рисков R сначала выбирается максимальный элемент:

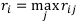
Затем из полученных элементов выбирается минимальный:

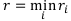
Соответствующая этому элементу финансовая операция объявляется наилучшей.

Итак, оптимальный элемент, выбранный по этому правилу, равен:

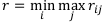
Исходя из финансового смысла выбора наилучшей финансовой операции по правилу Сэвиджа, его также можно назвать правилом крайнего пессимизма. Таким образом, r — это максимальный риск, если он действует по данному правилу.

По правилу Гурвица в каждой строке матрицы доходов Q сначала выбирается элемент 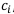, в соответствии с формулой:

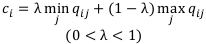
Здесь 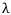-это весовой коэффициент, который выбирается в зависимости от предпочтений финансиста.

Затем из полученных элементов выбирается максимальный:

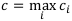
Этот элемент и объявляется наилучшим по правилу Гурвица с весом .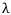

Рассмотрим два частных случая из этого правила:

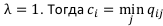1. ,т. е. приходим к правилу Вальда
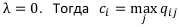2. , т. е. приходим к правилу розового оптимизма. Т. е. здесь финансист рассчитывает на самый благоприятных исход.

На практике обычно весовому коэффициенту придают значение вблизи 0,5. В этом случае правило Гурвица называют правилом взвешенного оптимизма.

Контрольная работа №22

Пусть дана следующая матрица доходов Q:

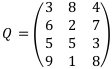
Решение:

Применим правило Вальда — найдём в каждой строке минимальный элемент.

Первая строка: 3

Вторая:2

Третья: 3

Четвёртая: 1.

Теперь из выбранных элементов найдём максимальный. Таких два — в первой и в третьей строке. Значит, по правилу Вальда наилучшими финансовыми операциями считаются .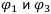

Теперь применим правило Сэвиджа. Составим матрицу рисок R:

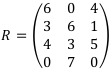
Теперь выберем максимальные элементы из каждой строки, и из них выберем минимальный. Это элемент 5 в третьей строке. Следовательно, по правилу Сэвиджа, наилучшей финансовой операцией будет.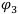

Наконец, применим правило Гурвица. За 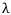примем 0,5.

Найдём элементы 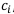по формуле: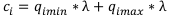

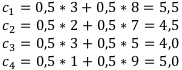
Максимальный элемент из найденных 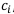— 5,5. Значит, по правилу Гурвица выходит, что наилучшей финансовой операцией будет 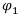. Это говорит о том, что операция 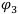наиболее характерна для экономиста-пессимиста, а если не сильно осторожничать, то лучше выбрать операцию .

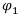Выбор наилучшей финансовой операции в условиях частичной определённости

В данной ситуации применяются следующие правила:

1. правило Байеса максимизации среднего ожидаемого дохода
2. правило Байеса минимизации среднего ожидаемого риска.

Предположим, что из статистики или других источников известны вероятности исходов 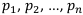. Здесь 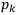— это вероятность -го исхода, 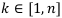. Если в матрице доходов Q или в матрице рисков R предусмотреть все возможные исходы, то сумма соответствующих вероятности должны ровняться 1:

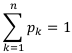
Правило Байеса максимизации среднего ожидаемого дохода.

Определим средний ожидаемый доход финансовой операции 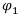как математическое ожидание случайной величины — вектора доходов по этой операции при всевозможных исходах. Этой случайной величине соответствует i-тая строка матрицы доходов Q.

Закон распределения этой дискретной случайной величины:

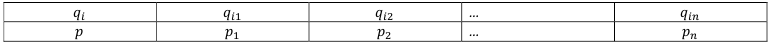
Математическое ожидание этой случайной величины выражается в виде скалярного произведения её значений на соответствующие вероятности:

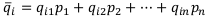
После того, как найдены средние ожидаемые доходы, по каждой финансовой операции набирается наибольшая величина:

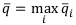
Соответствующая финансовая операция объявляется наилучшей.

Правило Байеса максимизации среднего ожидаемого риска.

Вместо матрицы доходов Q рассматривается матрица рисков R. По аналогии, каждую строку R можно рассматривать как случайную величину, имеющую следующий закон распределения:

Определяем средний ожидаемый риск как математическое ожидание случайной величины — вектора рисков по этой операции при всевозможных исходах. Этой случайной величине соответствует i-тая строка матриц R.

Математическое ожидание этой случайной величины выражается в виде скалярного произведения значений этой случайной величины на соответствующие вероятности:

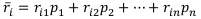
После подсчёта средних ожидаемых рисков по каждой финансовой операции выбирается наименьшее значение:

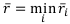
Соответствующая операция объявляется наилучшей.

С учётом частичной неопределённости дорешаем наш Пример 1:

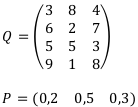
Матрица Р — это матрица вероятностей появления соответствующего исхода, т. е. 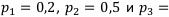0,3. Эти вероятности мы получили из статистики или какого-то другого источника.

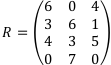
Найдём 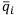по формуле 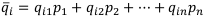и выберем среди найденных наибольший:

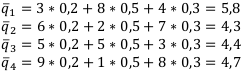
Наибольшим 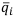будет 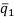Следовательно, по правилу Байеса максимизации ожидаемого дохода, наилучшей финансовой операцией становится .

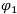Применим правило минимизации ожидаемых рисков — найдём 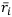по формуле 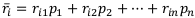и выберем среди найденных наименьший:

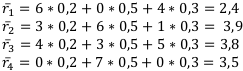
Наименьшим риском становится 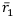, а значит, и по правилу минимизации ожидаемых рисков первая финансовая операция считается наилучшей. Т. е. получили ответ без противоречий. Если бы возникли противоречия, то следовало бы составить оптимальное множество Парето.

Вспомним формулы вычисления дисперсии:

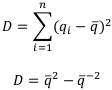
Среднее квадратичное отклонение равно квадратному корню из дисперсии и в финансовых расчётах называется средним ожидаемым риском: .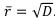

Диверсификация рисков

Предположим, у нас есть очень много денег, и есть, скажем, 5 банков. Понесём ли мы все деньги в один банк или распределим их между всеми пятью каким-либо образом? Скорее всего, мы выберем второе, чтобы в одночасье не потерять все деньги в случае неудачного выбора какого-то одного банка. Такое снижение рисков потерь и называется диверсификацией рисков.

При выборе наилучшей финансовой операции на первом этапе в условиях полной неопределённости целесообразно использовать известные правила (Вальда, Сэвиджа, Гурвица). На второй этапе, когда проясняется информация об исходах, целесообразно использовать правила Байеса. Эти правила указывают на наилучшую финансовую операцию. На третьем этапе при многовариантных расчётах целесообразно указать не одну, а несколько наилучших операций с вероятностями их выбора. В теории игр это называется решением игры в смешанных стратегиях.

Запишем матрицу Q доходов и матрицу? вероятности исходов.

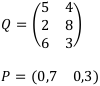
Вычислим доходы:

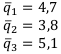
Теперь вычислим риски с учётом вероятностей. Находить их будем как СКО:

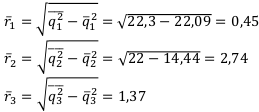
Получили операции:

Определим как 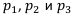вероятности самих финансовых операций, т. е. с какой вероятностью мы выбираем ту или иную финансовую операцию 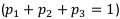. Другими словами, как часто мы выбираем ту или иную финансовую операцию. Тогда:

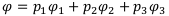
Нам нужно повлиять на эти вероятности так, чтобы максимизировать доход и минимизировать риски:

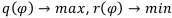
Видим, что первая операция у нас наиболее доходная и наименее рискованна, так что придадим наибольший вес ей — 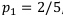, вторая операция наиболее рискованна, снизим её вероятность — 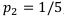, вероятность третьей операции получается .

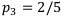Тогда: