Помощь по финансовой математике — решение заданий и задач онлайн

Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Как получить помощь в выполнении заданий по финансовой математике

Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.

Сколько стоит помощь

Стоимость помощи зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения

Минимальный срок выполнения составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить

Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Гарантии и исправление ошибок

В течение 1 года с момента получения Вами готового решения действует гарантия. В течении 1 года я и моя команда исправим любые ошибки.

Чуть ниже я предоставила теорию и формулы чтобы вы освежили знания и примеры оформления заказов по некоторым темам финансовой математики, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.

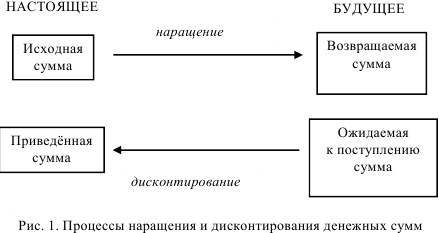
Наращение и дисконтирование денежных сумм

Финансовая математика — раздел количественного анализа финансовых операций, целью которого является решение широкого круга задач — от элементарного начисления процентов до анализа сложных кредитных и коммерческих операций.

Финансовая математика используется в банковском и сберегательном деле, страховании, в работе финансовых организаций, торговых фирм, инвестиционных компаний, фондовых и валютных бирж и т.п.

Возможно эта страница вам будет полезна:

Предмет финансовая математика

Фактор времени в расчетах

Важность учета фактора времени обусловлена принципом неравноценности денег, относящихся к различным моментам времени: равные суммы денег «сегодня» и «завтра» оцениваются по разному:

• во-первых, деньги можно продуктивно использовать во времени как приносящий доход финансовый актив, т.е. деньги могут быть инвестированы и тем самым принести доход ;
• во-вторых, инфляционные процессы ведут к обесцениванию денег во времени. Сегодня на рубль можно купить товара больше, чем завтра на этот же рубль, т.к. цены на товар повысятся;
• в-третьих, неопределенность будущего и связанный с этим риск повышает ценность имеющихся денег. Сегодня рубль в руке уже есть и его можно израсходовать на потребление, а будет ли он завтра в руке, — еще вопрос.

Существуют два подхода и соответствующие им два типа экономического мышления:

• статический подход не учитывает фактор времени, — в соответствии с этим, здесь возможно оперирование денежными показателями, относящимися к различным периодам времени, и их суммирование;
• динамический подход используется в финансовом анализе и финансовом менеджменте, где фактор времени играет решающую роль и его необходимо обязательно учитывать, поэтому здесь неправомерно суммировать денежные величины, относящиеся к различным моментам времени.

Эти два подхода соответствуют «бухгалтерскому» и «экономическому» принципам анализа затрат. Именно динамический подход предполагает включение в расходы так называемых неявных затрат, определяемых на основе принципа альтернативной ценности.

Простые процентные ставки

Процентные ставки называются простыми, если они применяются к одной и той же первоначальной денежной сумме в течение всего периода начисления.

При начислении процентных ставок используют два метода: метод наращения и метод дисконтирования.

Метод наращения по простым процентам

Метод наращения (accumulation)-определение денежной суммы в будущем, исходя из заданной суммы сейчас.

Метод наращения используется для простых ставок ссудных процентов, которые обычно применяются в краткосрочных операциях, когда интервал начисления совпадает с периодом и составляет, как правило, меньше года.

Введем обозначения:

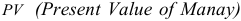— современная величина денег (первоначальная денежная сумма);

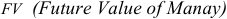— будущее значение денег (наращённая сумма);

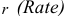-процентная ставка (относительная величина, т.е. 10%=0,1);

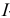— общая сумма процентов за весь период начисления;

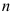— продолжительность периода начисления процента в годах.

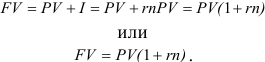
Тогда коэффициент наращения:

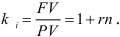
Обозначим через 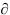— продолжительность периода начисления в днях, 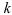— продолжительность года в днях тогда срок проведения операции корректируется по формуле

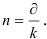
С учетом этого основная формула для определения наращенной суммы для краткосрочной операции, сроком менее одного года будет иметь вид:

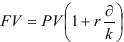
Пример оформления заказа №1.

Ссуда в размере 50 тысяч денежных единиц выдана на 6 месяцев по простой ставке процентов 28 % годовых. Определить наращенную сумму.

Решение:

Используем формулу

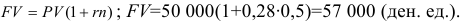
Ответ. Наращённая сумма равна 57 000 денежных единиц.

Замечание.

1. Относительно продолжительности финансовой операции договорились, что день выдачи и день погашения ссуды считать за один день.
2. По продолжительности года проценты подразделяются:

• на точные проценты, когда 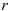= 365 или 366 дней, квартал = дня, месяц = 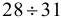день;
• обыкновенные проценты:

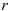= 360 дней, квартал = 90 дней, месяц = 30 дней .

3. В результате используют три схемы расчёта отношения :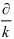

1) схема 365/365, называемая точными процентами (Англия, США). Для удобства выполнения расчетов пользуются сквозной нумерацией всех дней в году, представленной в табл.

2) схема 365/360, применяемая, например, в Бельгии, Франции;

3) схема 360/360 , называемая обыкновенными процентами (Германия, Дания, Швеция);

Приблизительное число дней проведения операций используется, когда не требуется большая точность, например, при частичном погашении займа, обыкновенный (коммерческий) процент более удобно использовать в аналитических расчетах. Точные проценты обычно используются в официальных методиках Центрального банка России.

Пример оформления заказа №2.

Кредит в размере 10 миллионов денежных единиц выдан 2 марта до 11 декабря под 30 % годовых. Год високосный. Определить размер наращенной суммы для различных вариантов расчета процента.

Решение:

Точный процент находим по формуле ;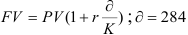

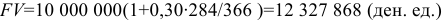
Коммерческий процент с точным числом дней в году найдем по формуле

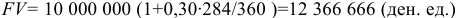
Коммерческий процент с приближенным числом дней в году найдем по формуле 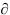=(30дн. • 8мес.=240)+(30 дн. — 5 дн. марта)+(11 дн. декабря)= 240+40=280;

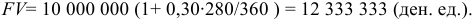
Пример оформления заказа №3.

Человеку, который инвестировал 100 000 денежных единиц, возмещено 101 000 денежных единиц девяноста днями позже. С какой годовой ставкой зарабатывались эти деньги при обыкновенном простом проценте?

Решение:

Итак, нам известны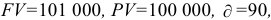

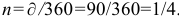. Воспользуемся формулой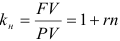

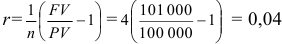или 4 % годовых.

Ответ. Процентная ставка равна 4 % годовых.

Метод дисконтирования по простым процентам

На практике часто приходится решать задачу, обратную наращению процентов. Расчет 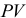по заданной 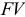называют дисконтированием суммы 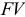. Процесс начисления процентов и их удержание в этом случае называют учетом, а сами удержанные проценты — дисконтом:

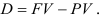
Величину 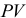, найденную с помощью дисконтирования, называют современной капитализированной стоимостью или компаундингом.

В зависимости от вида процентной ставки применяют два метода дисконтирования:

1) математическое дисконтирование — используется обычная процентная ставка ;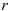

2) коммерческий (банковский учет) — применяется учетная процентная ставка .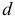

Математическое дисконтирование — формальное решение задачи, обратной наращению, т. е. из формулы

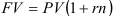
следует

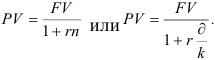
Пример оформления заказа №4.

Кредит выдается под простую ставку 26 % годовых на 250 дней. Рассчитать сумму, полученную заемщиком и дисконт (сумма процентных денег), если требуется вернуть 40 млн. денежных единиц.

Решение:

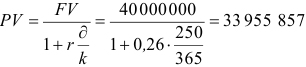(ден.ед.);

Тогда разность между будущей и текущей суммами будет равна: 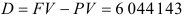(ден.ед).

Ответ. Сумма, полученная заемщиком, составит 33 955 857 денежных единиц, сумма процентных денег — 6 044 142 денежные единицы.

Банковский учет заключается в покупке денежных обязательств, например, векселя, банком по цене, которая меньше номинальной указанной в нем суммы.

Сумма, получаемая заемщиком вычисляется, как разность между суммой, которая должна быть возвращена и будущей суммой процентных денег (D), то есть

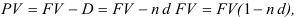
таким образом, .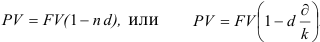

При дисконтировании по учетной ставке, чаще всего используют схему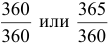

Пример оформления заказа №5.

Кредит выдается на полгода по простой учетной ставке 20 %. Рассчитать сумму, получаемую заемщиком, и дисконт D, если требуется вернуть 30 млн денежных единиц.

Решение:

Воспользуемся формулами:

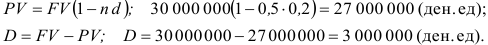
Ответ. Сумма, полученная заемщиком, составит 27 000 000 денежных единиц, сумма процентных денег — 3 000 000 денежных единиц.

В зависимости от применяемой ставки различают прямую и обратную задачи

Пример оформления заказа №6.

Вексель на 10 175 денежных единиц, погашаемый через 90 дней, продан банку, который установил 7 % процентную ставку простого процента при дисконтировании. Какой будет выручка?

Решение:

Замечание, Оформление денежных отношений между партнерами финансовой сделки может производиться при помощи ВЕКСЕЛЯ (расписки), которые, по существу, являются письменными обязательствами заплатить определенную сумму денег в установленный срок.

Когда вексель покупается до даты его погашения, цена 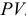, которую инвестор будет платить, определяется следующим образом: .

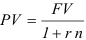Решение. Здесь 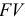= 10 175 ден. ед., 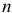= 90/360 = 1/4, 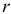=0,07, используя формулу 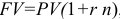, тогда

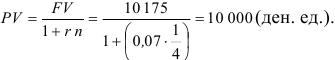
Ответ. Выручка составит 10 000 ден. ед.

Сложные процентные ставки

Применение схемы сложных процентов целесообразно в тех случаях, когда:

• проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга. Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процентов;
• срок ссуды более года.

Наращение по сложной процентной ставке

Пусть 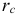— относительная величина годовой ставки сложных ссудных процентов. Тогда

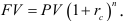
Пример оформления заказа №7.

Первоначальная сумма долга равна 50 млн денежных единиц. Определить наращенную сумму через 2.5 года по ставке 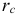=25% годовых.

Решение:

Используя формулу 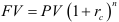, получим

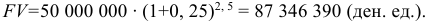
Графическая иллюстрация соотношения наращенной суммы по простым и сложным процентам представлена на рис. 2.

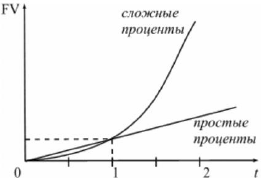
Как видно из рис., при краткосрочных ссудах начисление по простым процентам предпочтительнее, чем по сложным процентам; при сроке в один год разница отсутствует, но при среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам значительно выше, чем по простым.

Если ставка сложных процентов меняется во времени, формула наращения имеет вид:

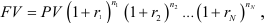
где 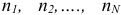— интервалы начисления, 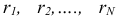— соответствующие им годовые процентные ставки.

Возможно эта страница вам будет полезна:

Примеры решения задач по финансовой математике

Пример оформления заказа №8.

В договоре зафиксирована переменная ставка сложных процентов, определяемая как 15% годовых плюс 6% в первые два года, 8% в третий год, 10% в четвертый год. Определить величину наращения за 4 года.

Решение:

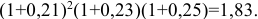. Ответ. Множитель наращения за 4 года составит 1,83.

Номинальная ставка процентов

Если сложные проценты начисляются несколько раз в году, то в этом случае используется номинальная годовая процентная ставка .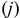

Пусть 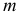— число интервалов начисления, 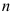— общее число лет, тогда проценты за каждый интервал начисления будут начисляться по ставке —, а 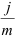наращенная сумма за весь период начисления составит

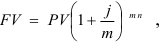
где 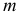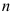— общее число периодов начисления процентов за весь срок проведения финансовой операции.

Чем чаще происходит начисление, тем больше наращенная сумма.

Пример оформления заказа №9.

В банк на депозитный счет вложены деньги в сумме 5 тыс. руб. сроком на два года с полугодовым начислением сложных процентов по ставке 20% годовых. Определить наращенную сумму и сравнить ее со случаем, если проценты начисляются ежеквартально.

Решение:

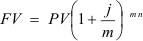
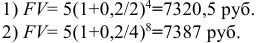
Ответ Наращенная сумма при полугодовом начислении процентов к концу двух лет составит 7320,5 руб., а при ежеквартальном -7387 руб.

Эффективная ставка процентов

Эффективной процентной ставкой называется ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке .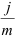

Выведем формулу для нахождения величины эффективной ставки. Из уравнения

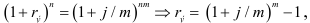
где 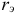— эффективная ставка.

Пример оформления заказа №10.

Каков размер эффективной ставки 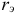, если номинальная процентная ставка 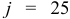% годовых при ежемесячном начислении процентов.

Решение:

.

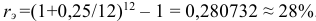Замечание: Для участвующих в сделке сторон безразлично применять ли 25 % ставку при ежемесячном начислении процентов или годовую (эффективную) ставку 28 %.

Ответ. Размер эффективной ставки составит 28 % годовых.

Непрерывные проценты

Наращенная сумма при дискретных процентах определяется по формуле весь период начисления составит

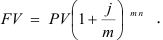
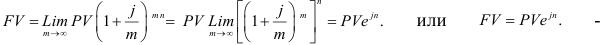
формула наращенной суммы при непрерывном начислении процентов, где 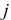— сила роста.

Непрерывное начисление процентов используется при анализе сложных финансовых задач, например, обоснование и выбор инвестиционных решений. Оценивая работу финансового учреждения, где платежи за период поступают многократно, целесообразно предполагать, что наращенная сумма непрерывно меняется во времени и применять непрерывное начисление процентов.

Непрерывным дисконтированием называется операция, обратная непрерывному наращению, т.е. уменьшение суммы в ejn раз за п лет

Дисконтирование по ставке сложных ссудных процентов

Математический учет. Известно, что будущая стоимость фиксированных периодических платежей находится по формуле:

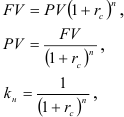
где 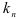— коэффициент наращения.

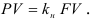
Пример оформления заказа №11.

Определить современную (текущую, настоящую) величину суммы 100 000 000 денежных единиц, выплачиваемую через 3 года при использовании ставки сложных процентов 24% годовых.

Решение:

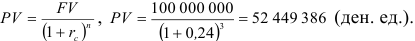
Ответ. Современная величина составит 52 449 386 денежных единиц.

Банковский учет.

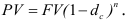
Определение величины процентных ставок

Из основной формулы для наращения суммы

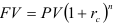
получаем формулу для вычисления годовой процентной ставки сложного ссудного процента:

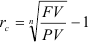
Формулу для номинальной годовой ставки можно получить из формулы:

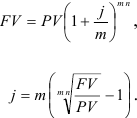
Пример оформления заказа №12.

Какова должна быть сложная процентная ставка ссудного процента, что бы первоначальный капитал утроился за 5 лет? Решить Задача так же для случая начисления процентов по полугодиям по номинальной процентной ставке.

Решение:

а)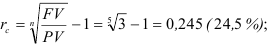

б)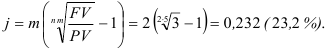

Ответ, а) сложная процентная ставка, при которой первоначальный капитал утроиться составляет 24,5 %; б) номинальная процентная ставка, при которой первоначальный капитал утроиться составляет 23,2 %.

Не забудьте, что дата выдачи и дата погашения считается за один день.

Определение срока проведения операции (по сложной ставке ссудных процентов).

Воспользуемся формулой 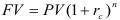. Прологарифмируем обе

части равенства

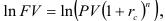
Получим

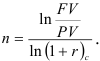
Аналогично можно получить формулы для вычисления сроков оплаты платежа по номинальной годовой ставке :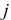

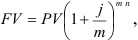
получим

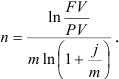
Логарифмы находятся по специальной таблице или вычисляются на калькуляторе.

Пример оформления заказа №13.

За какой срок первоначальный капитал в 50 000 000 денежных единиц увеличится до 200 000 000 денежных единиц, если:

а) на него будут начислены сложные проценты по ставке 28% годовых;

б) проценты будут начисляться ежеквартально по номинальной процентной ставке.

Решение:

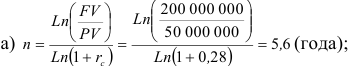
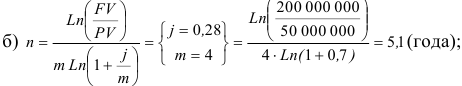
m — число интервалов начисления, j=0,28.

Ответ, a) 5,6 года; б) 5,1 года.

Эквивалентность процентных ставок различного типа

Эквивалентные процентные ставки — это такие процентные ставки, применение которых при одинаковых начальных данных дают одинаковые финансовые результаты.

Эквивалентные процентные ставки необходимо знать в случаях, когда возникает возможность выбора в условиях финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок.

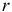— простая годовая ставка ссудного процента;

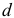— простая годовая учетная ставка;

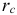— сложная годовая ставка ссудного процента;

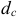— сложная годовая учетная ставка;

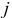— номинальная ставка ссудного процента;

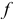— номинальная учетная ставка.

Замечание, 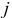и и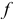спользуют, когда начисление процентов происходит не по годам, а раз в квартал, месяц, полугодие.

Запишем все известные формулы для определения наращённой суммы:

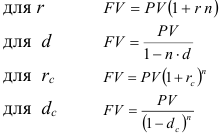
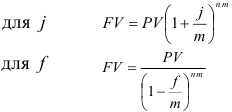
Приравнивая эти формулы попарно, можно получить соотношения, выражающие зависимость между любыми двумя различными ставками.

Например: Эквивалентность простых годовых ставок ссудного процента 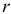и учетной ставки :

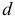Приравнивая формулы (3.1) и (3.2) получим

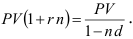
Следовательно

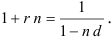
Отсюда

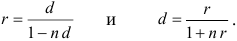
Пример оформления заказа №14.

Срок уплаты по долговому обязательству полгода. Учетная ставка равняется 18%. Какая будет доходность этой операции, измеренная в виде простой ставки ссудного процента. Найти гс.

Решение:

1 воспользуемся формулами (3.7)

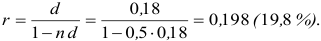
2) Из формул (3.1) и (3.3) получим

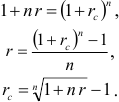
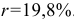. Воспользуемся полученными формулами:

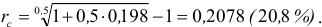
Ответ. Доходность операции, измеренная в виде простой ставки ссудного процента составит .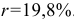

Доходность операции, измеренная в виде сложной ставки ссудного процента составит %.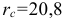

Начисление процентов в условиях инфляции

Инфляция — это обесценивание денег.

В экономике различают более 20 видов инфляции: инфляция, связанная с эмиссией денег; с большими кредитными расходами; превышения спроса над предложением; с ожиданием роста цен; с изменение цен на сырье; с ростом заработной платы и т.д.

Пусть S — некоторая сумма денег, имеющаяся у человека в данный момент; 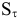— сумма денег через некоторое время t . Вследствие инфляции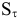 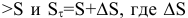— некоторая сумма денег, которая добавляется к S для сохранения стоимости годовой «потребительской корзины».

Основными показателями инфляции являются

1. средний годовой уровень инфляции
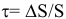
2. годовой индекс инфляции

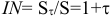
Годовой индекс инфляции показывает, во сколько раз возрастает цена «потребительской корзины» за год. При инфляции потребители ускоренно стараются материализовать деньги в товары, что в некоторой степени стимулирует производство, способствует более быстрому обороту денег и развитию экономики. Поэтому в последнее время инфляции не приписывают исключительно деструктивных качеств, так как развитие без инфляции приводит к накоплению денег и оттоку их из производства.

Учет инфляции

1) Простые проценты

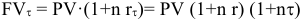
Тогда

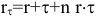
Пусть клиент делает вклад в размере PV в условиях инфляции с годовым уровнем 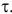. Банк обеспечивает ставку 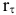. Какова реальная годовая процентная ставка прибыли ?

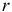Из (4.2) получаем

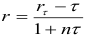
Следовательно, реальная покупательная стоимость будущего вклада составит

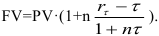
Пример оформления заказа №15.

Фирма договорилась с банком о выделении кредита размером 300 тыс. руб. сроком на полгода под 22% годовых без учета инфляции (проценты простые). Ожидаемый годовой уровень инфляции 14%. Какую процентную ставку с учетом инфляции возьмет банк, каков при этом коэффициент наращения и дисконт банка?

Решение:

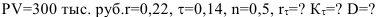
Процентная ставка с учетом инфляции:

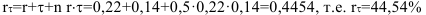
Коэффициент наращения:

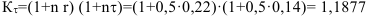
Наращенная сумма:

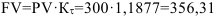тыс. руб. — такую сумму фирме придется вернуть банку с учетом инфляции.

Дисконт банка

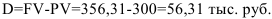
Без учета инфляции пришлось бы вернуть

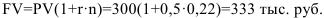
Ответ: процентная ставка с учетом инфляции 44,54%, при этом коэффициент наращения 1,1877 и дисконт банка 56,31 тыс. руб.

2) Сложные проценты

Пусть 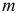— количество раз начисления процентов в году. Если известен средний коэффициент инфляции за 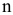лет 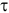, то наращенная сумма с учетом инфляции

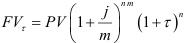
С другой стороны,

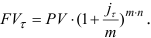
Из сравнения (4.3) и (4.4) получаем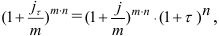

откуда

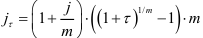
и

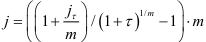
Пример оформления заказа №16.

Банк выдал ссуду в размере 80 тыс. руб. на три года с начислением процентов каждые полгода. Процентная ставка банка 28%. Среднегодовая инфляция ожидается на уровне 16%. Определите сумму, которую придется выплатить в конце срока, реальную ставку банка.

Решение:

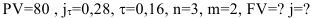
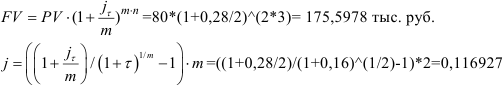
j=11,69% — по такой ставке банк получит реальный доход.

Ответ: 175, 5978 тыс.руб. сумма, которую придется выплатить в конце срока. 11,69% -реальная ставка банка.

Возможно эта страница вам будет полезна:

Курсовая работа по финансовой математике

Потоки платежей и финансовые ренты. Сущность потока платежей и основные категории

До сих пор мы рассматривали случаи финансовых операций, состоящих из отдельного разового платежа, например, получение и погашение долгосрочной ссуды. Вместе с тем, погашение такой ссуды возможно не только единовременным платежом, но множеством распределенных во времени выплат.

Последовательность периодических платежей называется потоком платежей.

Потоки платежей являются неотъемлемой частью всевозможных финансовых операций: с ценными бумагами, в управлении финансами предприятий, при осуществлении инвестиционных проектов, в кредитных операциях, при оценке бизнеса, при оценке недвижимости, выборе альтернативных вариантов финансовых операций и т. п.

Потоки платежей делятся:

• по распределению во времени — на регулярные (периодические) и нерегулярные;
• по величине элементов — на постоянные и переменные.

Периодические платежи могут осуществляться в конце периода — постнумерандо (обыкновенные) или в начале периода — пренумерандо.

Поток платежей, элементы которого одного знака и поступают через равные промежутки времени, называются финансовой рентой.

Существует три основных вида операций:

1. Срочным аннуитетом называется поток платежей с равными поступлениями С в течение ограниченного промежутка времени в конце каждого периода. Например, клиент вносит в банк первоначальную сумму, а в обмен получает серию периодических выплат в течение срока действия договора. В конце срока договора ему причитается получить сумму 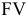. Эту ситуацию можно записать .
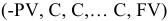2. Банковский кредит — это аннуитет наоборот. Клиент получает денежную ссуду 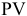, а потом выплачивает свой долг равными платежами С в течение срока погашения кредита. В конце срока операции ему остается выплатить сумму 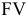. Эту ситуацию можно записать 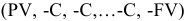и изобразить графически
3. Накопление периодическими взносами (формирование денежных фондов). В начале срока финансовой сделки вносится вклад в размере 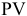и через равные промежутки времени к нему добавляются суммы С. К концу срока сделки с учетом начисленных процентов накопится сумма 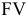. Эту ситуацию можно записать .

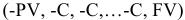Рента пренумерандо и постнумерандо

Пусть одинаковые платежи размером С (cost — стоимость) осуществляются пренумерандо в течение п периодов. На них нарастают проценты по номинальной (ежегодной) процентной ставке 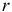. Сначала рассмотрим С по абсолютной величине.

В начале первого периода осуществлен взнос С. К концу периода на него нарастут проценты, и будущая сумма составит

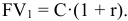
В начале второго периода внесена сумма С, а к концу второго периода на нее и на 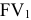опять нарастут проценты

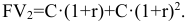
К концу третьего периода

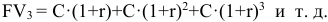
К концу n-ого периода будущая сумма составит

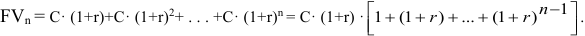
Нетрудно видеть, что это сумма геометрической прогрессии с общим членом

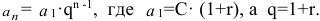
Как известно, сумма такой геометрической прогрессии

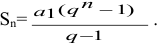
Таким образом, получаем

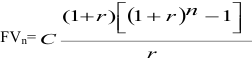
Если взносы осуществляются m раз в году в течение к лет, то число периодов сделки 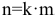, а процентная ставка за период составляет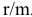

. В этом случае

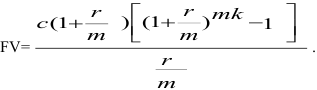
Те же условия, но рента вносится в конце каждого периода -постнумерандо.

К концу первого периода сделан взнос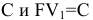

К концу второго периода снова сделан взнос С, а на 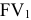наросли проценты:

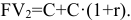
К концу третьего: 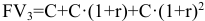и т. д.

Будущая сумма к концу n-ого периода

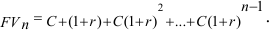
Это геометрическая прогрессия с первым членом 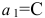и частным 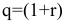. Следовательно,

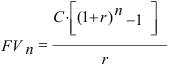
При выплатах пренумерандо абсолютная величина будущей накопленной суммы больше.

Если взносы осуществляются m раз в году в течение k лет, то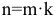

Возможно эта страница вам будет полезна:

Контрольная работа по финансовой математике

Пример оформления заказа №17.

Сколько денег можно накопить в банке в течение года, внося ежемесячно по 300 руб. во вклад под 18% годовых?

Решение:

?

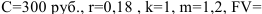1) взносы постнумерандо

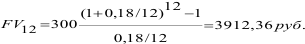
2) взносы пренумерандо

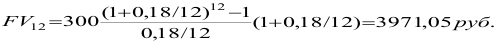
Если бы мы копили эти деньги дома, то в конце года имели бы только

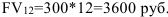
Таким образом, в обоих случаях за счет процентов банк нам приплачивает в конце года больше трехсот руб. Однако во втором случае (выплаты в начале каждого месяца) мы получим почти на 60 руб. больше.

Уравнение эквивалентности в общем виде

В повседневных финансовых операциях накопления денег, кредитования, аннуитета фигурируют как первоначальные, так и периодические взносы.

Все эти ситуации описываются общим эквивалентным уравнением:

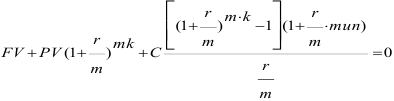
где тип=0, для взносов постумерандо,

тип=1, для взносов пренумерандо.

Из этого уравнения можно определить одну из величин как функцию остальных:

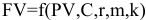1. — будущую сумму в любой момент;
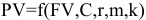2. — текущую сумму, пересчитанную к любому моменту финансовой сделки;
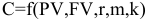3. — выплаты;
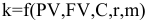4. — срок договора;
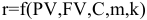5. — норму, годовую процентную ставку.

Определение будущей суммы

Пример оформления заказа №18.

Пусть в начале срока вложена сумма 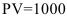руб. Ежемесячно вносится еще по 300 руб. Годовая процентная ставка 18%. Как при этом изменятся суммы в конце года постнумерандо и пренумерандо

Решение:

?

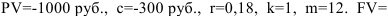1) Взносы постнумерандо.

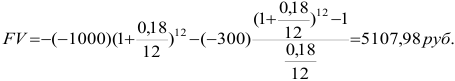
2) Взносы пренумерандо.

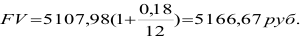
Ответ:

Определение текущей суммы

Из уравнения (3.1)

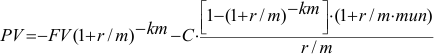
Пример оформления заказа №19.

Пенсионер получил наследство и хотел бы заключить договор с пенсионным фондом с условием получения 500 руб. в конце (начале) каждого месяца на протяжении 5 лет. Какая сумма обеспечит получение такого дохода при процентной ставке 24% годовых?

Решение:

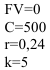
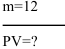
1) Выплаты в конце месяца (тип=0)

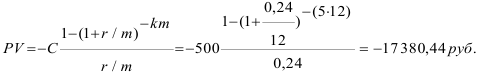
2) Выплаты в начале месяца (тип=1)

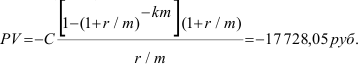
Как видим, во втором случае вклад должен быть значительнее почти на 350 руб. Знак минус показывает, что первоначальную сумму PV нужно отдать в банк.

Сколько денег пришлось бы пенсионеру положить в шкатулку, чтобы вынимать из нее по 500 руб. ежемесячно в течение 5 лет?

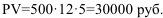
В обоих случаях банк за счет процентов доплачивает больше 12000 руб.

Определение периодических выплат

Какую сумму С нужно вносить регулярно в начале (в конце) периода, чтобы при первоначальном взносе PV и годовой процентной ставке 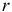через 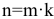периодов накопить капитал FV? Из (3.1) имеем

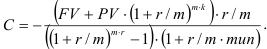
Пример оформления заказа №20.

Родители решили накопить за 18 лет на образование ребенка 50000 руб. Банк обеспечивает 6% годовых по вкладу. Сколько денег нужно вносить в конце каждого месяца?

Решение:

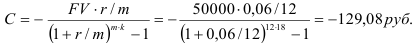
За 18 лет родители внесут в банк 129,08-18-12=27881,28 руб.

Остальные 50000 — 27881,28=22118,72 руб. доплатит банк.

Расчет срока ренты

Решая уравнение (3.1) относительно числа лет к, получим

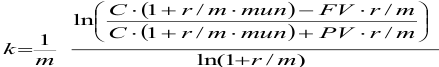
Пример оформления заказа №21.

Фирме нужно выплатить долг 300 млн. руб. ежегодными платежами по 111,52 млн. руб. Процентная ставка согласно договору между кредитором и фирмой установлена 12% годовых. Нужно определить срок платежа.

Решение:

Фирма выплачивает долг, пока сумма его не станет равной

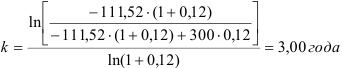
За это время с учетом процентов фирма выплатит сумму

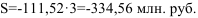
Переплата по процентам составит 34,56 млн. руб.

Возможно эта страница вам будет полезна:

Заказать работу по финансовой математике

Определение размера процентной ставки

Необходимость в определении величины процентной ставки возникает всякий раз, когда речь идет о выяснении эффективности (доходности) соответствующей финансово — банковской или коммерческой(деят-ть по продаже товаров и услуг) операции. Вопрос стоит так, под какую процентную ставку 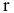нужно дать кредит в сумме PV, чтобы при периодических выплатах С через и периодов получить обратно сумму FV? Однако, расчет ставки по остальным параметрам ренты не так прост. Величина г не выражается в явном виде из уравнения (3.1). Поэтому необходимо решить нелинейное уравнение (3.1) относительно г. Раньше его решали методом линейной интерполяции или итерационным методом. Сейчас эта задача и все остальные примеры и задачи, легко решаются с помощью финансовых функций в Excel.

Нерегулярные потоки платежей

В финансовых операциях возможны ситуации, когда величина платежа либо увеличивается, либо уменьшается с течением времени, например, под влиянием инфляции. В таких случаях говорят о нерегулярных потоках платежей.

Один из способов расчета -это прямой счет, т.е. вычисление соответствующих характеристик по каждому платежу и последующему их суммированию.

Пример оформления заказа №22.

По приведенным данным о денежных потоках рассчитать для каждого наращенную величину, если потоки имеют место в конце года. Процентная ставка 12% годовых.

Решение:

Для решения данной задачи произведем прямой расчет наращенной суммы по каждому периоду, представив данные в виде таблиц.

Наращение суммы для потока А:

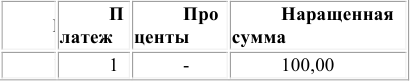
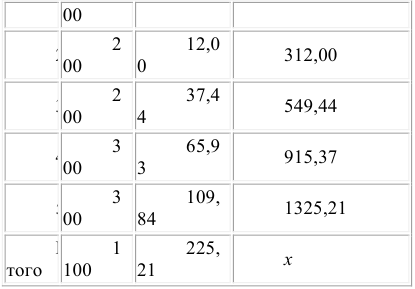
Таким образом, наращенная сумма потока А через пять лет составит 1’325,21 рублей.

Наращение суммы для потока В

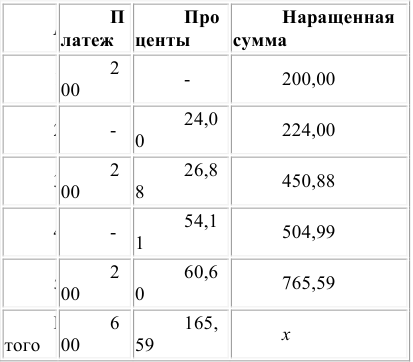
Для потока В наращенная сумма через пять лет составит 765,59 рублей.

Оценка эффективности инвестиционных проектов

Выгодные инвестиции — один из основных факторов влияющих на повышение рентабельности предприятия

Инвестиции — это долгосрочные финансовые вложения экономических ресурсов с целью создания и получения выгоды в будущем.

Инвестиционный процесс — это последовательность связанных инвестиций, растянутых во времени, отдача от которых также распределена во времени.

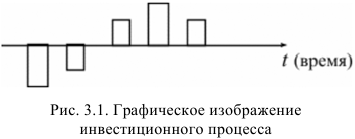
Принято различать:

• финансовые инвестиции;
• реальные инвестиции;
• инвестиции в нематериальные активы.

Финансовые инвестиции — вложение денежных средств в ценные бумаги; реальные инвестиции — вложения в основной капитал и прирост запасов; вложения в нематериальные активы — вложения в развитие научных исследований, повышение квалификации работников, приобретение лицензий и прав.

Реализация инвестиционных проектов требует отказа от денежных средств сегодня в пользу получения дохода в будущем, поэтому любой инвестиционный проект требует анализа и оценки.

Оценивая эффективность инвестиционных проектов, следует учитывать и степень риска, — здесь, как правило, выделяют два вида риска: предпринимательский и финансовый.

Предпринимательский риск — риск, связанный с деятельностью конкретного бизнеса. Финансовый риск — изменениями рыночной ставки дохода на капитал.

Для упрощения исследования эффективности инвестиций предполагается, что необходимая норма прибыли задана и одинакова для всех инвестиционных проектов и для любого из рассматриваемых проектов степень риска одинакова.

Важнейшая задача анализа инвестиционных проектов — расчет будущих денежных потоков, возникающих при реализации проекта.

В анализе инвестиционных проектов крупных и средних фирм в основном используют четыре основанные на дисконтировании показателя:

• чистый приведенный доход;
• индекс рентабельности инвестиций;
• внутреннюю норму доходности;
• дисконтированный срок окупаемости.

1.Чистый приведенный доход NPV (net present value)

Метод расчета чистого приведенного дохода основан на сопоставлении величины исходной инвестиции IC с общей суммой дисконтированных чистых денежных поступлений PV, генерируемых ею в течение прогнозируемого срока n. Т.к. приток денежных средств распределен во времени, он дисконтируется по ставке d, установленной инвестором.

Пусть делается прогноз, что инвестиция IC будет генерировать в течение n лет годовые доходы 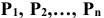. Тогда сумма дисконтированных доходов

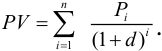
Чистый приведенный доход

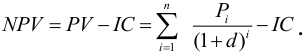
Правило:

Если NPV > 0, то проект следует принять, иначе его следует отклонить.

Основное достоинство этого метода: показатели NPV различных проектов можно суммировать

Пример оформления заказа №23.

Фирма собирается вложить средства в приобретение нового оборудования, стоимость которого вместе с доставкой и установкой составит 100 000 ден. ед. Ожидается, что внедрение оборудования обеспечит получение на протяжении 6 лет чистых доходов в 25 000, 30 000, 35 000, 40 000, 45 000, и 50 000 ден. ед. соответственно. Принятая норма дисконта равна 10%. Определить экономическую эффективность проекта.

Решение:

Изобразим ежегодные поступления от инвестиций на временной оси.

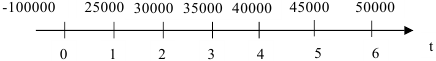
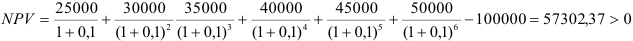
проект следует принять.

Как видим, при условии правильной оценки денежного потока проект обеспечивает возмещение произведенных затрат (примерно к концу четвертого года) и получение 10% чистой прибыли, а также дополнительной (сверх установленной нормы) прибыли, равной величине NPV=57 302,37.

Пример оформления заказа №24.

Проект, требующий инвестиций в размере 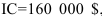, предполагает получение годового дохода в размере Рк=30 000$ на промежуток n = 15 лег. Оценить целесообразность такой инвестиции, если коэффициент дисконтирования 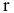=15%.

Решение:

Обратите внимание на тот факт, что все ежегодные поступления одинаковы, поэтому можно принять при расчете формулу современной стоимости ренты.

Рассчитаем чистый приведенный доход проекта:

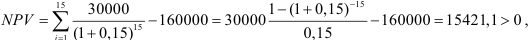
проект следует принять.

Индекс рентабельности инвестиций PI (profitability index)

Индекс рентабельности PI рассчитывается по формуле:

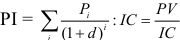
Правило:

Если 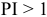, то проект следует принять, иначе его следует отклонить.

Этот относительный показатель, удобен при выборе одного проекта из ряда альтернативных, имеющих одинаковый NPV, либо при комплектовании портфеля инвестиций с максимальным суммарным NPV.

Норма рентабельности инвестиции IRR (Internal rate of return)

Под нормой рентабельности (внутренней нормой доходности) IRR инвестиции понимают значение коэффициента дисконтирования, при котором чистый приведенный эффект проекта равен нулю, т.е. IRR = d, при котором NPV ( d ) = 0.

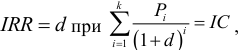
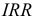показывает максимально допустимый относительный уровень доходов, которые могут быть ассоциированы с данным проектом.

Например, если проект полностью финансируется за счет ссуды коммерческого банка, то 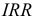показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которой делает проект убыточным.

На практике IRR сравнивается с 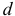— заданной нормой дисконта, которая отражает минимум возврата на вложенный в его деятельность капитал.

Правило:

Если 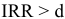, то проект следует принять, иначе его следует отклонить.

Пример оформления заказа №25.

Найдите 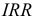денежного потока: -100, +230, -132.

Решение:

Схему вложения денег изобразим на временной оси.

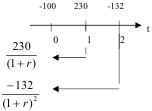
Воспользовавшись определением 1RR:

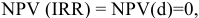
составим уравнение для нахождения этого показателя

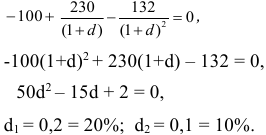
Для данного проекта существуют две ставки внутренней доходности.

Эти ставки показывают, что все финансовые операции по ставке выше IRR = 20% и по ставке ниже IRR = 10% убыточны для рассматриваемого проекта.

Срок окупаемости инвестиций DPP (Discounted Pay Period)

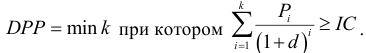
Дисконтированный срок окупаемости инвестиций — это показатель, оценивающий характерное время инвестиции, а именно определяющих, как быстро инвестиционные расходы будут возмещены доходами.

Недостатки: не определяется рентабельность проекта, не принимается во внимание величина и направления распределения денежных потоков на протяжении периода окупаемости: рассматривается только период покрытия расходов в целом.

Пример оформления заказа №26.

Дисконтированный срок окупаемости инвестиций при переменной норме дисконта. Размер инвестиции — $12800. Доходы от инвестиций в первом году: $7360: во втором году: $5185; в третьем году: $6270. Размер барьерной ставки — 11,4% в первом году; 10,7% во втором году; 9,5% в третьем году. Определите дисконтированный срок окупаемости инвестиционного проекта.

Решение:

Пересчитаем денежные потоки в вид текущих стоимостей:

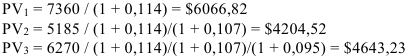
Определим период по истечении которого инвестиция окупается.

Сумма дисконтированных доходов за 1 и 2 года: 6066,82 + 4204,52 = $10271,34, что меньше размера инвестиции равного S12800.

Сумма дисконтированных доходов за 1,2 и 3 года: 10271,34 + 4643,23 = $15454,57, что больше $12800, это значит, что возмещение первоначальных расходов произойдет раньше 3 лет.

Если предположить что приток денежных средств поступает равномерно в течении всего периода, то можно вычислить остаток от третьего года.

Остаток = (1 — (15454,57 — 12800)/4643,23) = 0,4289 года

Ответ: период окупаемости в текущих стоимостях равен 3 годам (точнее 2,43 года).

В странах с нестабильной политической, налоговой, законодательной системах показатель дисконтированный срок окупаемости инвестиций имеет одно из главных значений с точки зрения снижения финансовых рисков. Полный инвестиционный анализ не должен ограничиваться одним показателем. Желательно использовать их комбинацию

Кредиты. Погашение долга единовременным платежом

Количественный анализ долгосрочной задолженности (займа) применяется для достижения сбалансированности, т.е. адекватности его параметров принятым условиям финансового соглашения, путем планирования погашения долга.

Планирование погашения долга заключается в определении периодических расходов, связанных с займом, — такие расходы называются обслуживанием долга. Разовая сумма обслуживания долга — срочная уплата, в которую входят:

• текущие процентные платежи;
• средства, для погашения (амортизации) основной суммы долга.

Размеры срочных уплат зависят от условий займа:

• срока;
• наличия и продолжительности льготного периода;
• уровня процентной ставки;
• способа погашения основной суммы долга и выплаты процентов.

Для кредитной схемы в качестве исходных параметров выступают величина займа 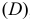, срок его погашения 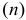, процент по кредиту 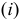, под который выдаются деньги, и поток платежей по выплате долга .

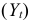Рассмотрим различные способы погашения задолженности, поскольку от выбора способа погашения стоимость кредита (сумма выплачиваемых процентов) будет различной. Здесь возможны два варианта:

• а) погашение единовременным платежом, т.е. возврат всей суммы в оговоренный срок;
• б) погашение долга в рассрочку, т.е. частями.

Погашение основной суммы долга единовременным платежом в конце срока с постоянной выплатой процентов

Рассмотрим погашение единовременным платежом. В простейшем случае кредит погашается единым платежом в конце срока:

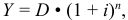
где 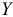— срочная уплата;

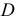— сумма долга.

Этот платеж, как наращенная сумма долга, состоит из двух частей:

• возврат основной суммы долга ;
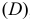• выплата процентов по долгу 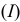, где

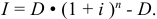
В финансовой практике встречаются случаи, когда у кредитора возникает необходимость вернуть часть денег досрочно. В таких случаях возникает риск невозврата, поскольку требуемой суммы на такой момент времени может и не быть.

При значительной сумме долга разовый платеж требует создания так называемого фонда погашения, путем периодических взносов. Фонд погашения аккумулирует денежные средства, направленные на погашение задолженности. Наиболее эффективно размещение фонда погашения с начислением на взносы процентов, например, на специальном счете в банке. Такие платежи по своей сути являются финансовой рентой (аннуитетом), поэтому задача сводится к определению одного из параметров финансовой ренты — члена ренты.

Здесь возможно два варианта.

Первый — выплата процентов по мере их начисления, а основная сумма денег возвращается в конце срока займа.

Если проценты выплачиваются ежегодно, тогда величина срочной уплаты (расходов должника по погашению долга) равна:

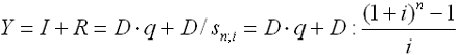
где 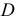— первоначальная сумма долга;

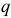— ставка процентов по условиям займа;

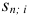— коэффициент наращения финансовой ренты;

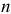— срок долга в годах;

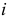— ставка процентов при создании фонда погашения.

Здесь фигурируют две ставки процентов: 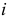— определяет скорость роста суммы фонда погашения; 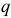— сумму выплачиваемых за заем процентов.

Пример оформления заказа №27.

Долг 100 тыс. долларов выдан под 10% годовых на 3 года, с ежегодной выплатой процентов по долгу. Для погашения суммы долга единовременным платежом создается фонд, куда ежегодно вносятся равные суммы, на которые начисляются проценты по ставке 11%. Найти ежегодные расходы должника.

Решение:

Ежегодные расходы должника составляют величину срочной уплаты:

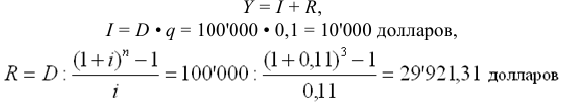
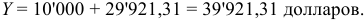
Ответ: ежегодные расходы должника по обслуживанию долга составят 39’921,31 долларов.

Однако, более наглядным и эффективным способом планирования долга является составление таблиц, в которых отражают все основные характеристики обслуживания долга:

План погашения долга единовременным платежом с ежегодной выплатой процентов и созданием погасительного фонда

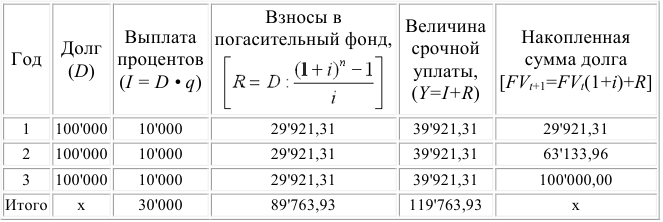
Таким образом, из приведенной таблицы видно, что ежегодные расходы по обслуживанию долга составят 39’921,31 долларов, что в целом за три года составит сумму 1 19’763,93 долларов, причем выплата процентов за три года 30’000 долларов, а на погашение основного долга в размере 100’000 долларов приходится всего лишь 89’763,93 долларов, т.е. 10’236,07 долларов является набежавшими процентами на размещенные средства в фонде погашения.

Таким образом, создание фонда погашения является необходимым элементом составления плана погашения долга, т.к. позволяет не только снизить риск не возврата денежных средств, но и сократить расходы по обслуживанию суммы долга.

Погашение основной суммы долга и процентов по нему единовременным платежом в конце срока ссуды

Второй вариант погашения долга единовременным платежом состоит в выплате процентов одновременно с погашением долга.

В этом случае взносы в фонд погашения являются одновременно и величиной срочной уплаты (членом финансовой ренты):

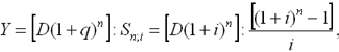
где 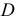— первоначальная сумма долга;

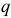— ставка процентов по условиям займа;

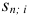— коэффициент наращения финансовой ренты;

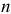— срок долга в годах;

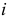— ставка процентов при создании погасительного фонда.

Пример оформления заказа №28.

Рассмотрим предыдущий пример, изменив условия: погашение единовременным платежом, как суммы основного долга, так и выплаты процентов.

Решение:

Величина срочной уплаты равна:

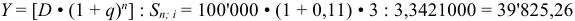долларов

Ответ: величина ежегодных расходов по обслуживанию долга составит 39’825,26 долларов, что несколько меньше аналогичного показателя в предыдущей задаче, следовательно, меньше и общая сумма расходов по обслуживанию долга, составляющая величину 119’475,78 долларов.

Для более наглядного представления плана погашения долга здесь также необходимо составление таблицы.

План погашения долга единовременным платежом

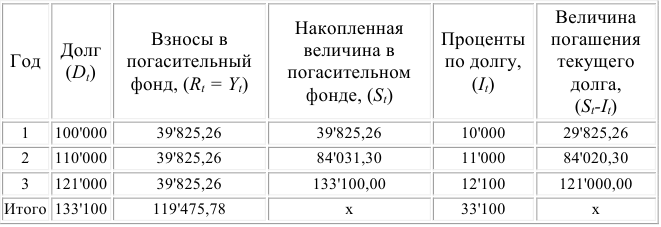
Как видно из таблицы, происходит ежегодное увеличение суммы долга за счет присоединения к нему процентов, поэтому к концу срока долг возрастет до 133’100 долларов, из которых выплата процентов составит 33’100 долларов. Однако за счет увеличения размера взносов в погасительный фонд общая величина обслуживания долга уменьшается.

Погашение долга в рассрочку

В практике финансовой деятельности долг часто погашается в рассрочку, т.е. распределенными во времени платежами. При погашении основной суммы долга частями его текущее значение будет уменьшаться и, следовательно, сумма процентных платежей также будет уменьшаться.

Погашение долга частями также может осуществляться различными способами. В зависимости от преследуемых интересов стороны могут выбирать различные, удобные для них режимы в виде постоянных или переменных финансовых рент, а также нерегулярных потоков платежей.

Погашение основной суммы долга равными частями

Одним из вариантов погашения долга в рассрочку является погашение основной суммы долга равными частями.

При этом величина погашения долга определяется след, образом:

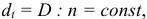
где 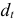— величина погашения основной суммы долга;

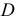— первоначальная сумма долга;

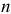— срок долга в годах;

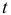— номер года, .

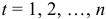Проценты начисляются на уменьшаемую сумму основного долга:

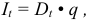
где 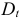— остаток долга на начало очередного года; 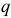— ставка процентов, начисляемых на сумму долга. Тогда размер срочной уплаты можно представить как сумму процентов и сумму погашения долга:

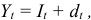
где 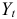— срочная уплата на конец текущего года.

Пример оформления заказа №29.

Сумма 100 тыс. долларов выдана под 10% годовых на 3 года. Определить величину срочной уплаты при погашении основной суммы долга равными ежегодными частями.

Решение:

Величина суммы погашения долга равна:

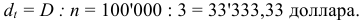
Поскольку величина срочной уплаты при таком способе погашения долга меняется из года в год, то в этом случае без построения плана погашения долга в виде таблицы просто не обойтись.

План погашения основной суммы долга равными частями

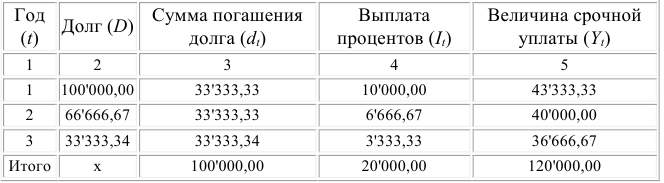
Ответ: общие расходы по обслуживанию долга составили 120 тыс. долларов, из которых 20 тыс. долларов составляют проценты, а 100 тыс. долларов — погашение основной суммы долга.

Погашение долга и процентов по нему равными суммами в течение срока ссуды

Долг также можно погашать в рассрочку равными срочными уплатами, которые включают в себя как погашение основной суммы долга, так и величину процентов по нему:

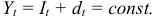
При погашении долга в рассрочку величина долга систематически убывает, что приводит к уменьшению процентов и, соответственно, увеличению сумм, идущих на погашение долга, — это так называемое прогрессивное погашение.

Поскольку срочные уплаты равны, то их последовательность представляет собой финансовую ренту, современное значение которой должно быть равно сумме долга.

По формуле для определения размера платежа постоянной годовой финансовой ренты с выплатами в конце периода, размер срочной уплаты равен:

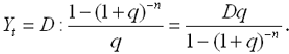
где 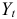— величина срочной уплаты;

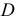— первоначальная сумма долга;

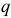— процентная ставка на сумму долга;

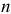— срок долга в годах;

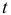— номер года, .

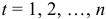Пример оформления заказа №30.

Условия предыдущей задачи, но погашение долга предусматривает уплату равными срочными выплатами.

Решение:

Срочная уплата, включающая в себя погашение основной суммы долга и выплату процентов по долгу, равна:

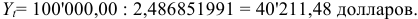
Отсюда общие расходы по погашению долга равны:

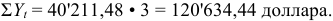
Ответ: ежегодные расходы по погашению долга будут составлять 40’211,48 долларов, а за весь срок финансовой операции — 120’634,44 доллара.

При этом варианте погашения долга также возможно построение таблицы.

План погашения долга равными срочными уплатами

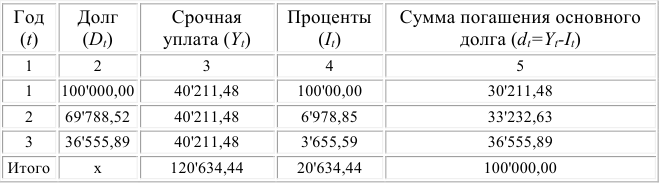
Таким образом, общие расходы по обслуживанию долга составляют 120’634,44 долларов, из которых 100 тыс. долларов идут на погашение долга, а 20’634,44 долларов — проценты. В таблице наглядно представлено распределение суммы срочной уплаты на выплату процентов и непосредственное погашение долга.

Потребительский кредит

Частным случаем погашения долга равными срочными уплатами является потребительский кредит, при котором проценты начисляются сразу на всю сумму кредита, а сумма задолженности равномерно погашается на протяжении всего срока кредита. Проценты в потребительском кредите начисляются сразу на всю сумму долга по простой ставке:

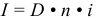
Тогда общая сумма расходов по погашению кредита складывается из выплаты процентов и суммы основного долга:

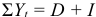
Следовательно, размер срочной уплаты определяется по формуле:

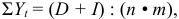
где 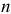— срок кредита в годах; 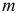— количество взносов в течение года.

Пример оформления заказа №31.

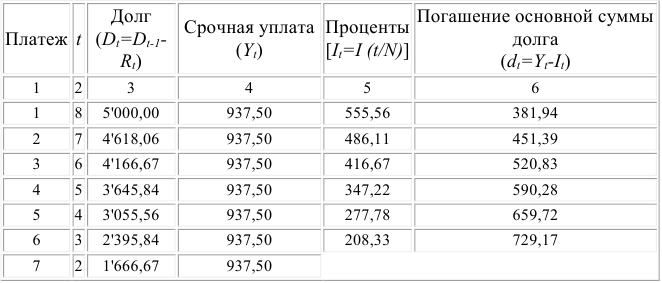
Потребительский кредит на сумму 5 тыс. руб. открыт на 2 года по ставке 25% годовых. Погашение кредита равными взносами ежеквартально. Определить стоимость кредита и размер ежеквартальных взносов.

Решение:

Стоимость кредита — это проценты, которые равны:

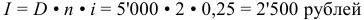
Общая сумма расходов по обслуживанию кредита равна:

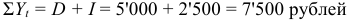
Ежеквартальные взносы составят величину:

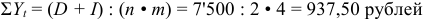
Таким образом, ежеквартальные взносы в размере 937,50 рублей позволяет выплатить сумму долга и выплатить проценты.

Если бы использовалось прогрессивное погашение, т.е. начисление процентов на остаток долга, то это было бы заметно дешевле для должника.

Расчленение величины срочной уплаты в потребительском кредите на процентные платежи и погашение основной суммы долга в мировой практике называется «методом 78». Это связано с тем, что для потребительского кредита сроком 12 месяцев и ежемесячным погашение, сумма порядковых номеров месяцев будет равна 78, что и дало название такому методу начисления процентов.

Это правило можно обобщить для лет и 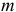платежей в году:

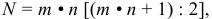
где N — сумма последовательных номеров выплат.

Отсюда очень легко расчленить срочную уплату на процентные платежи и сумму погашения основного долга:

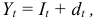
где 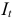— процентный платеж;

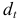— сумма погашения основного долга.

Тогда величина процентного платежа определяется следующим образом:

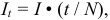
а сумма погашения основного долга как разница срочной уплаты и процентных выплат:

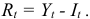
Рассмотрим предыдущий пример, расчленив срочную уплату на составляющие элементы, все данные представив в виде таблицы.

План погашения потребительского кредита