Оглавление:
Цель: формирование умения составлять уравнения кривых второго порядка и выполнять их изображение.
Задание для самостоятельной внеаудиторной работы:
8.1. Выучите определения окружности, эллипса, параболы, гиперболы. Используя обобщающую таблицу, проанализируйте, с помощью каких уравнений задаются кривые второго порядка, каковы основные параметры каждой линии.
8.2. Определите вид кривой второго порядка и постройте ее:
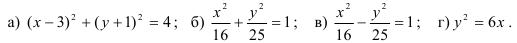
8.3. Составьте уравнение кривой второго порядка по следующим условиям:
а) уравнение окружности с центром в точке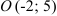 
и радиусом 3;
б) уравнение окружности с центром в точке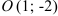 
, проходящей через точку 
;
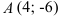в) уравнения эллипса, большая полуось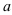 
которого равна 3, малая полуось 
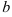равна 1;
г) уравнение гиперболы, действительная полуось 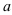которой равна 6, мнимая полуось 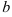равна 2;
д) уравнение параболы, имеющей фокус в точке (1; 0);
е) уравнение параболы, уравнение директрисы которой имеет вид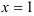 
.
8.4. Определите вид кривой второго порядка и постройте ее:
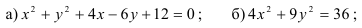
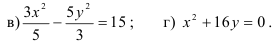
Методические указания по выполнению работы:
Кривая второго порядка — линия на плоскости, задаваемая уравнением: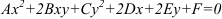 
, где коэффициенты 
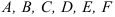— любые действительные числа при условии, что 
одновременно не равны нулю.
Выделяют следующие кривые второго порядка:
- Окружность — множество точек плоскости, равноудаленных от одной точки, называемой центром.
- Эллипс — множество точек на плоскости, сумма расстояний от каждой из которых до двух заданных точек (называемых фокусами) есть величина постоянная (большая, чем расстояние между фокусами).
- Гипербола — множество точек плоскости, разность расстояний от каждой из которых до двух заданных точек (называемых фокусами) есть величина постоянная (меньшая, чем расстояние между фокусами).
- Парабола — множество точек плоскости, равноудаленных от заданной точки (называется фокусом) и данной прямой (называется директрисой).
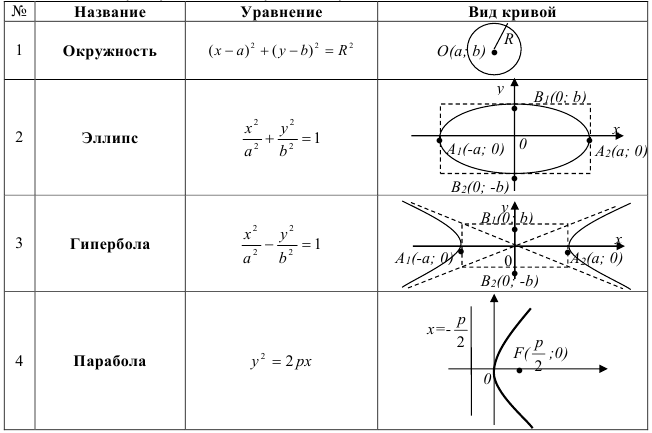
Для того чтобы по заданному уравнению определить вид кривой второго порядка, удобно использовать следующую обобщающую таблицу:
Рассмотрим примеры решения типовых задач.
Пример 1.
Составьте уравнение окружности с центром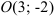 
и радиусом 
.
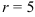Решение:
Подставив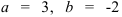 
и 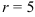в каноническое уравнение окружности 
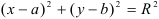, получим: 
.
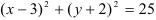Пример 2.
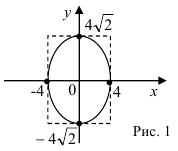
Постройте эллипс, заданный уравнением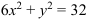 
.
Решение:
Приведем уравнение эллипса к каноническому виду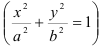 
, для этого разделим все члены уравнения на 32, добиваясь того, чтобы в правой части была 1:
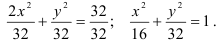
При сравнении с каноническим видом отмечаем, что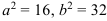 
, откуда 
.
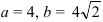Эллипс будет иметь вид (рис. 1):
Пример 3.
Постройте гиперболу, заданную уравнением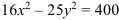 
.
Решение:
Приведем уравнение к каноническому виду. Для этого разделим все его члены на 400: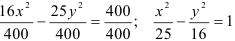 
.
Из этого уравнения можем записать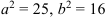 
, т.е. 
, 
.
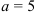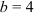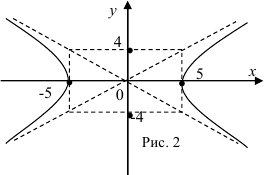
Выполним чертеж (рис. 2). Отметим, что ветви гиперболы будут стремиться к асимптотам, в качестве которых выступают диагонали прямоугольника со сторонам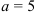и и .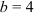
Пример 4.
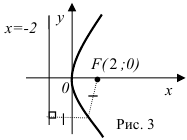
Найдите координаты фокуса и уравнение директрисы параболы, заданной уравнением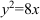 
и постройте её.
Решение:
Из канонического уравнения параболы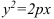 
следует, что 
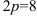, т.е. 
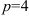, откуда 
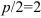. Значит, точка 
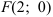— фокус параболы, а 
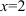— уравнение ее директрисы.
На основании определения: любая точка параболы равноудалена от фокуса и директрисы, — схематически строим график параболы (рис. 3).
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
