Задание: Полное исследование функции и построение графика.
Цель: формирование умения проводить полное исследование функции и стоить её график.
Задание для самостоятельной внеаудиторной работы:
18.1. Выполните домашнюю контрольную работу №1.
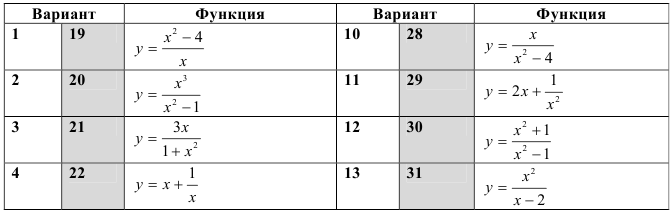
Проведите полное исследование функции и постройте её график.
Методические указания по выполнению работы:
При исследовании функции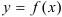 
используйте следующую схему:
1. Найдите область определения функции (если функция представляет собой дробь, то знаменатель дроби должен быть отличен от нуля).
2. Исследуйте функцию на четность-нечетность:
- если
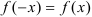, то функция четная (график четной функции симметричен относительно оси 
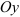); - если
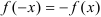, то функция нечетная (график нечетной функции симметричен относительно начала координат); - в противном случае функция ни четная, ни нечетная.
3. Исследуйте функцию на периодичность (среди изучаемых нами функций периодическими могут быть только тригонометрические функции).
4. Найдите точки пересечения графика функции с осями координат:
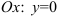(решаем уравнение лишь в том случае, если можем использовать известные нам методы);
.
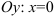5. Найдите первую производную функции и критические точки (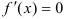
или 
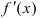не существует).
6. Найдите интервалы монотонности, точки экстремума и экстремумы функции.
7. Найдите вторую производную функции и критические точки (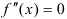
или 
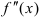не существует).
8. Найдите интервалы выпуклости, вогнутости графика функции, точки перегиба.
9. Найдите асимптоты графика функции.
10. Постройте график функции. Для этого задайте систему координат и выполните следующие действия:
- отметьте точки экстремума и экстремумы функции (найдены в п.6), причем рекомендуется прямо на чертеже обозначить поведение графика функции в окрестности этих точек дугами:
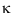или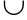 
; - отметьте точки перегиба (найдены в п.8);
- отметьте точки пересечения графика функции с осями координат (найдены в п.4);
- постройте асимптоты графика функции пунктирными линиями (найдены в п.9);
- пользуясь полученными данными о промежутках возрастания, убывания, выпуклости и вогнутости, постройте график функции с учётом его поведения вблизи асимптот:
- проверьте, соответствует ли график функции результатам проведенного исследования.
11. Выберите контрольные точки вблизи точек экстремума, найдите соответствующие значения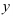 
, проверьте правильность построения графика.
Если при выполнении домашней контрольной работы возникают вопросы, разберите решение аналогичного примера:
Постройте график функции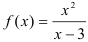 
.
Решение:
1. Данная функция определена на всей числовой прямой за исключением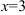 
, т.к. в этой точке знаменатель обращается в ноль.
2. Для определения четности и нечетности функции найдем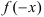 
:
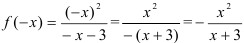. Видим, что 
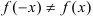и 
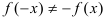, следовательно, функция 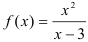ни четная, ни нечетная.
3. Функция непериодическая.
4. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью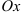 
примем 
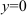. Получим уравнение: 
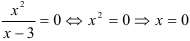. Итак, точка (0; 0) — точка пересечения с осями координат.
5. Найдем производную функции по правилу дифференцирования дроби:
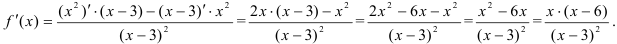
Для нахождения критических точек первого рода найдем точки, в которых производная функции равна 0 или не существует.
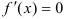, если 
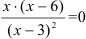, следовательно, 
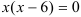. Произведение тогда равно 0, когда хотя бы один из множителей равен 0: 
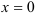или 
.
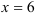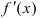не существует, если знаменатель 
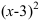равен 0, т.е. 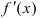не существует при .
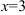Итак, функция имеет три критические точки первого рода: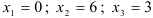 
.
6. На числовой оси отметим критические точки первого рода, причем точку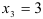 
отмечаем выколотой точкой, т.к. в ней функция не определена.
Расставляем знаки производной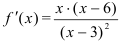 
на каждом промежутке:
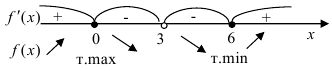
На промежутках, где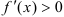 
, исходная функция возрастает (при 
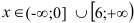), где 
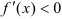— убывает (при 
).
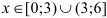Точка 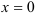является точкой максимума функции. Для нахождения максимума функции найдем значение функции в точке 0: 
.
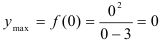Точка 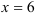является точкой минимума функции. Для нахождения минимума функции найдем значение функции в точке 6: 
.
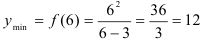7. Найдем вторую производную функции как производную от первой производной:
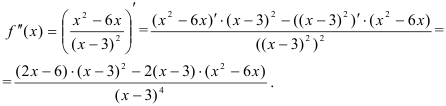
Вынесем в числителе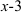 
за скобки и выполним сокращение:
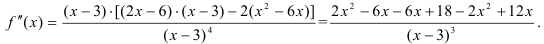
Приведем в числителе подобные слагаемые: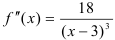 
.
Найдем критические точки второго рода: точки, в которых вторая производная функции равна нулю или не существует.
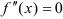, если 
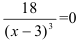. Данная Дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет.
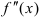не существует, если знаменатель 
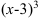равен 0, т.е. 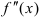не существует при .
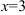Итак, функция имеет одну критическую точку второго рода: .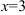
8. Найдем интервалы выпуклости и точки перегиба графика функции.
На числовой оси отметим критическую точку второго рода выколотой точкой, т.к. в ней функция не определена.
Расставляем знаки второй производной 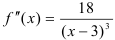на каждом промежутке:
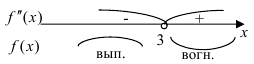
На промежутках, где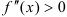 
, исходная функция вогнута (при 
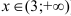), где 
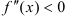— выпукла (при 
).
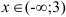Точка 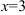не является точкой перегиба графика функции, т.к. в ней исходная функция не определена.
9. Найдем асимптоты графика функции.
9.1. Поскольку область определения функции — все действительные числа за исключением 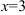, то проверим, является ли прямая 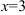вертикальной асимптотой. Для этого вычислим предел функции 
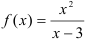в точке 
.
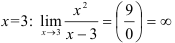Получили, что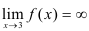 
, следовательно, 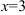— вертикальная асимптота.
9.2. Для поиска горизонтальных асимптот находим 
.
Поскольку в пределе фигурирует неопределенность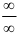 
, воспользуемся правилом Лопиталя:
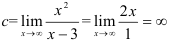. Т.к. 
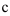— бесконечность, то горизонтальных асимптот нет.
9.3. Для поиска наклонных асимптот находим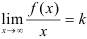 
:
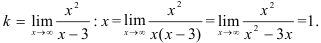
Итак,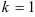 
. Найдем 
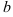по формуле: 
.
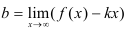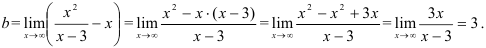
Получили, что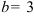 
. Тогда 
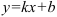— наклонная асимптота. В нашем случае она имеет вид: 
.
Таким образом, данная функция имеет вертикальную асимптоту 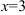и наклонную асимптоту .
10. По полученным ранее данным строим график функции . Поскольку к построению графика предъявляются высокие требования, система координат должна быть задана корректно: должно присутствовать обозначение осей 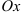, , начало отсчета, единицы измерения по каждой оси.
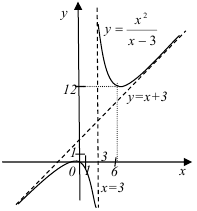
- отметим экстремальные точки: (0;0) — вершина дуги , (6; 12) -вершина дуги ;
- проведём асимптоты графика функции: 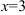и пунктирными линиями;
- пользуясь полученными данными о промежутках возрастания, убывания, выпуклости и вогнутости, построим график функции.
11. Для более точного построения можно выбрать несколько контрольных точек. Например, найдем значения функции в точках -2 и 7:
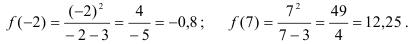
Корректируем график функции с учетом контрольных точек.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
