Оглавление:
Задание: Определение промежутков выпуклости, вогнутости графика функций, нахождение точек перегиба.
Цель: формирование умения находить промежутки выпуклости, вогнутости графика функции и его точки перегиба.
Задание для самостоятельной внеаудиторной работы:
16.1. Выучите определения вогнутого и выпуклого на интервале графика функции, точки перегиба. Запомните критерий выпуклости (вогнутости) графика функции.
16.2. Выясните, в чем заключается достаточное условие существования точек перегиба. Детально изучите и постарайтесь освоить алгоритм, позволяющий находить промежутки выпуклости (вогнутости) графика функции и точки перегиба.
16.3. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции:
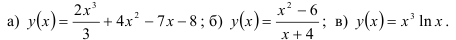
16.4. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции 
.
16.5. Определите, при каком значении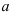 
график функции 
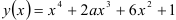будет вогнутым на области определения функции.
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
График функции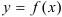 
называется вогнутым на интервале 
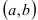, если он расположен выше любой касательной к графику функции на данном интервале.
График функции 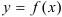называется выпуклым на интервале 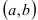, если он расположен ниже любой касательной к графику функции на данном интервале.
Точка графика непрерывной функции, в которой меняется характер выпуклости, называется точкой перегиба.
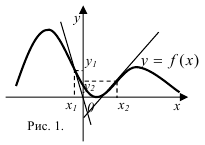
Функция может иметь несколько интервалов выпуклости и вогнутости, несколько точек перегиба. При определении промежутков выпуклости и вогнутости в качестве ответа выбирают интервал значений: точки перегиба не относят ни к промежуткам выпуклости, ни к промежуткам вогнутости.
Так, график функции на рис.1, является выпуклым на промежутках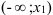 
и 
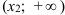; вогнутым на 
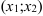. График функции имеет две точки перегиба: 
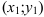и 
.
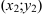Критерий выпуклости-вогнутости функции: если функция 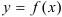имеет положительную вторую производную, то график функции на интервале 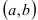вогнутый;
- если функция 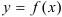имеет отрицательную вторую производную, то график функции на интервале 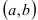выпуклый.
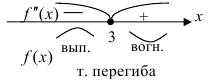
Критерий выпуклости-вогнутости функции удобно представляется в виде схемы:
Таким образом, исследовать функцию на выпуклость-вогнутость означает найти те интервалы области определения, в которых вторая производная сохраняет свой знак.
Критическими точками функции второго рода называются те точки, в которых вторая производная равна нулю или не существует. Только критические точки могут быть точками перегиба. Для их нахождения используется следующая теорема:
Теорема (достаточное условие существования точек перегиба). Если вторая производная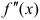 
при переходе через точку 
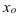меняет знак, го точка графика с абсциссой 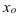является точкой перегиба.
При исследовании функции 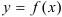на выпуклость-вогнутость и точки перегиба удобно использовать следующий алгоритм:
- Найдите область определения функции.
- Найдите первую производную функции
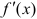. - Найдите вторую производную функции .
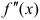- Определите критические точки второго рода (
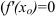или 
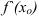не существует). - На числовой оси отметьте критические точки второго рода и определите знаки второй производной на каждом из получившихся интервалов.
- Найдите интервалы выпуклости-вогнутости графика функции, используя соответствующие критерии; выпишите абсциссы точек перегиба (если они есть) и найдите значение функции в этих точках.
Пример 1.
Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции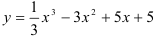 
.
Решение:
1. Данная функция определена на множестве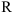 
.
2. Найдем первую производную функции: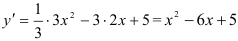 
.
3. Найдем вторую производную функции: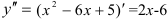 
.
4. Определим критические точки второго рода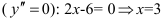 
.
5. На числовой оси отметим критическую точку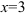 
. Она разбивает область определения функции на два интервала 
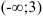и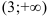 
. Расставим знаки второй производной функции 
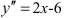на каждом из полученных интервалов:
при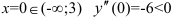 
;
при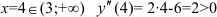 
.
6. Согласно критерию выпуклости-вогнутости график функции 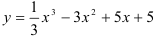выпуклый при 
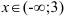, вогнутый при 
.
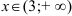Значение 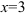— абсцисса точки перегиба. Вычислим значение функции при :
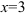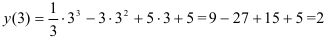. Итак, точка с координатами (3;2) — точка перегиба.
Ответ: график функции 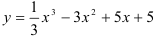выпуклый при ,
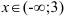вогнутый при 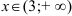; (3;2) — точка перегиба.
Пример 2.
Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции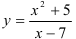 
.
Решение:
1. Данная функция определена в том случае, когда знаменатель отличен от нуля: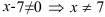 
.
2. Найдем первую производную функции:
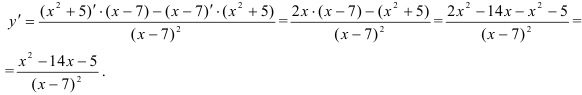
3. Найдем вторую производную функции: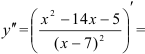 
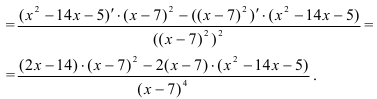
Вынесем в числителе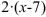 
за скобки:
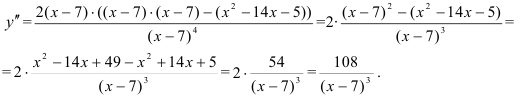
4. Определим критические точки второго рода: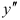 
не может быть равна нулю, поскольку числитель дроби 
.
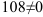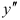не существует, если 
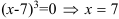— критическая точка второго рода.
5. На числовой оси отметим критическую точку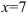 
выколотой точкой, поскольку в этой точке функция 
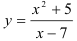не определена. Эта точка разбивает область определения функции на два интервала 
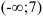и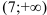 
. Расставим знаки второй производной функции 
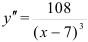на каждом из полученных интервалов:
при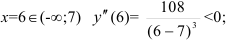 
при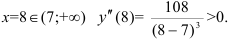 
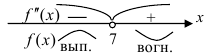
6. Согласно критерию выпуклости-вогнутости график функции 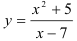является выпуклым при 
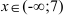, вогнутым при 
.
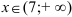Точка с абсциссой 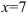не может быть точкой перегиба, т.к. в этой точке функция не существует (терпит разрыв).
Ответ: график функции 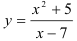выпуклый при 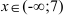, вогнутый при .
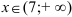На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
