Задание: Нахождение определённых интегралов методом подстановки.
Цель: формирование умения находить определённые интегралы методом подстановки.
Задание для самостоятельной внеаудиторной работы:
27.1. Разберите, в чём заключается сущность использования метода подстановки в определённом интеграле.
27.2. Найдите определённые интегралы как интегралы от «некоторых сложных» функций и методом подстановки:
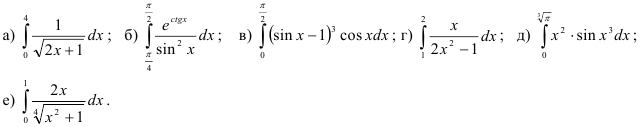
Лейбниц успел сделать чрезвычайно много в различных областях науки. Как ему это удалось? Просто он имел способность работать в любом месте, в любое время и при любых условиях. Он много читал, записывал и постоянно думал. Большинство математических работ Лейбница написаны в тряских колымагах, переносивших его по Европе XVII века. Результатом этой активности стала масса исписанных бумаг всех размеров и сортов, которые он так и не разобрал и не опубликовал. Сейчас большинство из них хранится в Ганноверской библиотеке, ожидая своих исследователей.
Лейбница мы можем по-праву назвать гениальным немецким философом, математиком, юристом и дипломатом. В 1700 году он основал Берлинскую Академию наук и стал её первым президентом. Но, как ни покажется странным, нет трудов Лейбница, написанных на родном немецком языке. Почему так? Лейбниц считал, что в его эпоху немецкий был недостаточно очищен от варваризма, чтобы быть пригодным для выражения на нём математических и философских мыслей.
Выполнив задание 27.2 и заменив получившиеся ответы буквами из таблицы, Вы узнаете, на каком языке (помимо французского) были написаны труды Готфрида Вильгельма Лейбница.
Язык:
Карта ответов:
27.3. Найдите определённые интегралы:
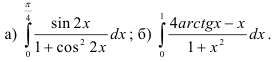
Методические указания по выполнению работы:
Интегрирование подстановкой (заменой переменной) — осуществляется с использованием формулы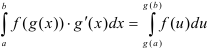 
.
Для нахождения определенного интеграла методом подстановки (замены переменной) целесообразно использовать следующий алгоритм:
- Введите новую переменную
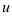таким образом, чтобы под знаком интеграла стояла функция, содержащая 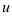(от этой функции должен существовать табличный интеграл), и производная 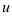. - Найдите
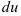по формуле: 
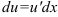. - Выразите
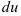через . - Найдите новые границы интегрирования
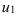и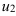 
, подставив исходные границы в функцию 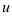. - Подставьте 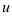и в исходный интеграл. Если подстановка выполнена верно, то произойдет сокращение одинаковых множителей и интеграл сведется к табличному относительно переменной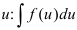
. Смените границы интегрирования на 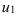и 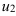. - Пользуясь таблицей неопределённых интегралов, возьмите полученный определенный интеграл с переменной .
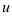Рассмотрим применение метода замены переменной на примере.
Пример 1.
Вычислите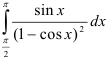 
.
Решение:
1. Выполним подстановку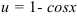 
с целью прийти к интегралу от функции 
.
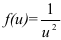2. Найдем 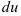по формуле 
.
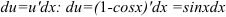3. Выразим из выражения пункта 2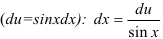 
.
4. Вычислим новые границы интегрирования для переменной 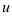. Для этого подставим существующие границы 
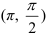в выражение .
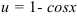Тогда нижняя граница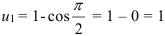 
; верхняя граница 
.
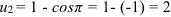5. Подставим 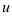и в исходный интеграл (пока неопределенный):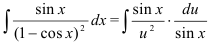 
.
Видим, что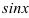 
можно сократить и прийти к интегралу относительно переменной 
.
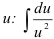В результате всех преобразований первоначальный интеграл примет вид: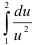 
.
6. Вычислим полученный интеграл. По таблице интегралов находим, что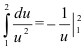 
. Воспользуемся свойством 3 определенного интеграла, позволяющим менять границы интегрирования, при этом избавляясь от знака «минус» перед определенным интегралом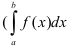 
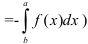. Тогда 
.
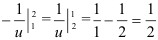Ответ: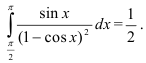 
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
