Оглавление:
Задание: Нахождение неопределённых интегралов методом по частям.
Цель: формирование умения находить неопределённые интегралы методом по частям.
Задание для самостоятельной внеаудиторной работы:
24.1. Проанализируйте, в чём заключается сущность метода интегрирования по частям. Разберите алгоритм нахождения неопределённого интеграла методом по частям. Ответьте на
контрольные вопросы:
- В чем заключается сущность метода интегрирования по частям?
- Приведите формулу метода интегрирования по частям.
- В каких типах интегралов целесообразно использовать метод интегрирования по частям? Что принимать за
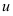, а что за 
?
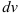24.2. Найдите интегралы методом по частям:
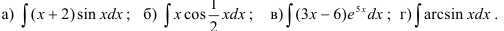
24.3. Найдите интегралы:
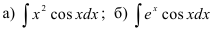(указание: за 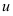обозначьте 
); 
.
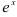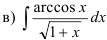Методические указания по выполнению работы:
При вычислении интеграла методом по частям подынтегральное выражение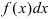 
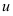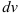представляют в виде произведения двух множителей и , причем 
обязательно входит в 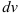. Далее пользуются формулой интегрирования по частям: 
.
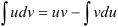Существуют интегралы, которые удобно находить методом интегрирования по частям:
- В интегралах вида
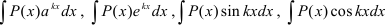, где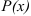 
— многочлен, 
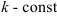, за 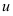принимают многочлен 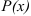, остальные множители — за 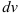. - Если в подынтегральной функции один из множителей — логарифмическая или обратные тригонометрические функции
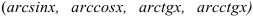, то их обозначают за 
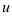, остальные множители — за .
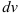Для нахождения неопределенного интеграла методом по частям используйте следующий алгоритм:
- Разбейте подынтегральное выражение на 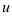и 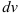(в соответствии с правилом, рассмотренным выше).
- Найдите
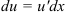и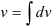 
. - Подставьте
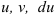и 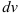в формулу 
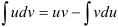и возьмите получившийся интеграл.
Рассмотрим применение метода интегрирования по частям на примерах.
Пример 1.
Найдите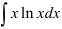 
.
Решение:
1. Поскольку под знаком интеграла встречается логарифмическая функция, то ее принимаем за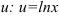 
. Остальные множители принимаем за 
.
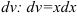2. Находим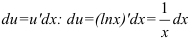 
.
Находим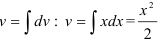 
(полагаем 
).
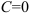3. Воспользуемся формулой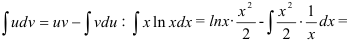 
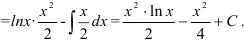
Ответ: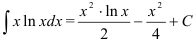 
.
Пример 2.
Найдите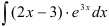 
.
Решение:
1. Исходный интеграл имеет вид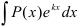 
, следовательно, за 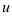принимают многочлен 
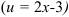остальные множители — за 
.
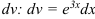2. Находим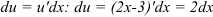 
.
Находим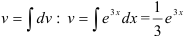 
(полагаем ).
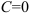3. По формуле 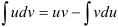имеем: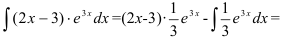 
.
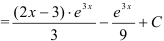Ответ: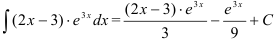 
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
