Оглавление:
Матрицы и определители
Задание: Нахождение определителей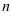 
-го порядка, миноров и алгебраических дополнений.
Цель: формирование умения находить определители второго, третьего и четвертого порядка, вычислять миноры и алгебраические дополнения элементов определителя.
Задание для самостоятельной внеаудиторной работы:
Запомните, какова методика нахождения определителей второго, третьего и четвертого порядка. Выучите, что называют минорами и алгебраическими дополнениями элементов определителя.
3.2. Вычислите определитель:
3.3. Выучите, какими основными свойствами обладает определитель.
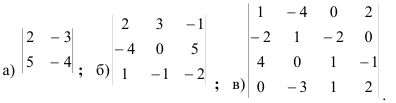
3.4. Вычислите определитель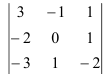 
. Используя свойства определителей, найдите определитель:
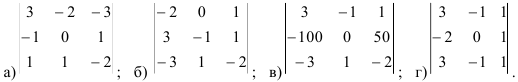
3.5. Найдите миноры и алгебраические дополнения элементов второй
строки определителя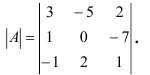 
3.6. Вычислите определитель:
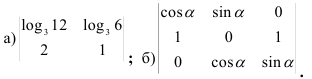
3.7. Решите уравнение и неравенство:
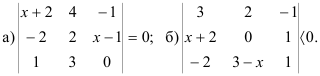
Методические указания по выполнению работы:
Каждой квадратной матрице можно поставить в соответствие некоторое число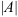 
, называемое её определителем, следующим образом:
1. Второго порядка: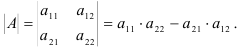 
2. Третьего порядка:
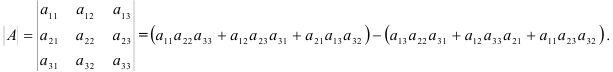
3. Любого порядка. Определитель равен сумме произведений элементов любой строки или столбца определителя на их алгебраические дополнения:
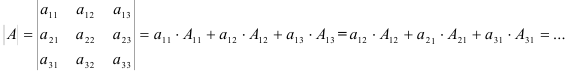
где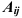 
— алгебраическое дополнение элемента 
: 
;
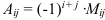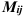— минор элемента — новый определитель порядка 
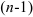, полученный из 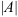вычеркиванием 
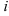-й строки и 
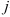-го столбца, на пересечении которых находится элемент .
Свойства определителей:
1. Определитель не изменится, если его строки заменить столбцами и наоборот (свойство равноправности строк и столбцов).
2. При перестановке двух строк или столбцов определитель меняет свой знак на противоположный.
3. Определитель с двумя одинаковыми строками или столбцами равен нулю.
4. Общий множитель всех элементов строки или столбца можно вынести за знак определителя.
Следствие: Если элементы двух строк или столбцов определителя пропорциональны, то определитель равен нулю.
Приведем примеры нахождения определителей второго, третьего и четвертого порядков:
Пример 1.
Найдите определитель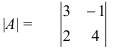 
Решение:
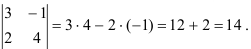
Ответ: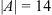 
.
Пример 2.
Найдите определитель матрицы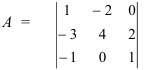 
Решение:
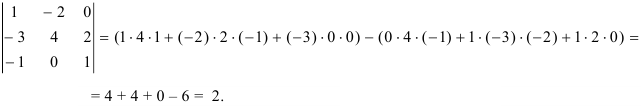
Ответ: 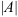= 2.
Для нахождения определителя четвертого порядка необходимо уметь вычислять миноры и алгебраические дополнения элементов определителя.
Пример 3.
Найдите миноры и алгебраические дополнения элементов третьего столбца определителя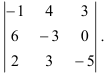 
Решение:
1. Минор элемента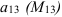 
получаем вычеркиванием из определителя первой строки и третьего столбца:
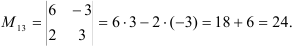
2. Алгебраическое дополнение элемента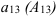 
найдем по формуле: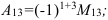 
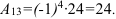
3. 
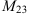получаем вычеркиванием из определителя второй строки и третьего столбца:
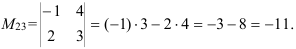
4. 
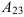найдем по формуле: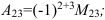 
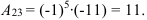
5. 
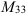получаем вычеркиванием из определителя третьей строки и третьего столбца:
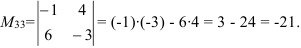
6. 
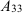найдем по формуле: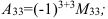 
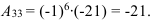
Ответ: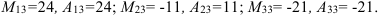 
Пример 4.
Вычислите определитель четвертого порядка: 
Решение:
1. Разложим определитель по элементам первой строки: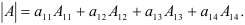 
Так как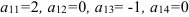 
, то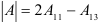 
.
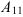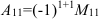2. Вычислим алгебраическое дополнение 
:
, где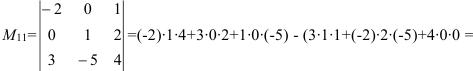 
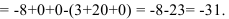
Тогда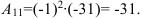 
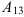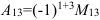3. Вычислим алгебраическое дополнение 
:
, где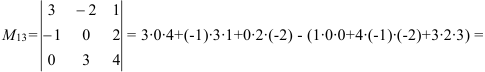 
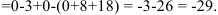
Тогда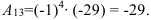 
4. Поскольку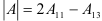 
, получим: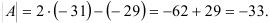 
Ответ: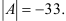 
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:
