Для решения некоторых задач действительных чисел может оказаться недостаточно и поэтому возникает необходимость в расширении множества действительных чисел. Попробуем, например, решить уравнение
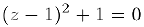
Действительных решений оно не имеет, однако формально мы можем найти его корни, если введем в рассмотрение символ
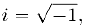
который мы назовем мнимой единицей. Тогда из данного уравнения следует, что
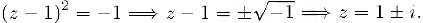
Введем теперь следующее важное
Определение 1. Комплексным числом называется выражение вида
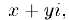
где 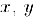 — действительные числа,
— действительные числа, 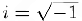 — мнимая единица.
— мнимая единица.
Множество всех комплексных чисел мы обозначим через С.
Для комплексного числа 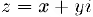 действительные числа и у называются, соответственно, его действительной и мнимой частями. Обозначаются действительная и мнимая части, соответственно, через
действительные числа и у называются, соответственно, его действительной и мнимой частями. Обозначаются действительная и мнимая части, соответственно, через  . Комплексные числа
. Комплексные числа 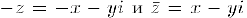 называются, соответственно, противоположным и сопряженным к комплексному числу
называются, соответственно, противоположным и сопряженным к комплексному числу 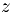 . Используя эту терминологию можно сказать, иго приведенное выше квадратное уравнение имеет пару комплексно-сопряженных корней
. Используя эту терминологию можно сказать, иго приведенное выше квадратное уравнение имеет пару комплексно-сопряженных корней 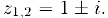 .
.
Комплексное число, мнимая часть которого равна нулю, т.е. число вида 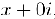 , которое мы будем обозначать через х, отождествляется с действительным числом х и, таким образом, множество действительных чисел R является подмножеством множества комплексных чисел С или, иначе, множество комплексных чисел является расширением множества действительных чисел. Здесь уместно отметить, что « формулированная идея расширения множества действительных чисел до комплексных оказалась чрезвычайно плодотворной как в самой математике, так и в ее приложениях, например, в физике, механике, электротехнике, где аппарат комплексных чисел очень активно используется.
, которое мы будем обозначать через х, отождествляется с действительным числом х и, таким образом, множество действительных чисел R является подмножеством множества комплексных чисел С или, иначе, множество комплексных чисел является расширением множества действительных чисел. Здесь уместно отметить, что « формулированная идея расширения множества действительных чисел до комплексных оказалась чрезвычайно плодотворной как в самой математике, так и в ее приложениях, например, в физике, механике, электротехнике, где аппарат комплексных чисел очень активно используется.
Комплексное число с нулевой действительной частью, а. именно, число  , которое мы будем записывать как
, которое мы будем записывать как 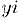 , называется чисто мнимым.
, называется чисто мнимым.
Два комплексных числа считаются равными, если действительная и мнимая части одного из них равны, соответственно, действительной и мнимой частям другого.
Чтобы иметь возможность использовать комплексные числа, следует определить алгебраические операции над ними. Этим мы сейчас и займемся.
Пусть 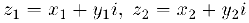 — два комплексных числа.
— два комплексных числа.
Суммой комплексных чисел 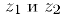 называется комплексное число
называется комплексное число 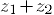 , которое находится сложением соответствующих выражений:
, которое находится сложением соответствующих выражений:
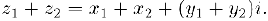
Тогда разностью этих комплексных чисел называется число 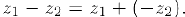 .
.
Произведением комплексных чисел 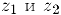 называется комплексное число
называется комплексное число 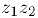 . которое мы можем найти, перемножив выражения для данных комплексных чисел и учитывая при этом, что
. которое мы можем найти, перемножив выражения для данных комплексных чисел и учитывая при этом, что 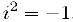 . В результате получим:
. В результате получим:
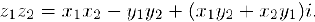
Прямой проверкой мы можем убедиться в том, что операции сложения и умножения комплексных чисел обладают свойствами коммутативности, ассоциативности и дистрибутивности, сформулированными для действительных чисел (глава IV, §1, свойства 1). 2). 5)). Роль комплексных. единицы и нуля выполняют действительные числа 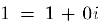 и
и  .
.
Чтобы определить операцию деления комплексных чисел, покажем сначала, что для любого 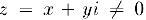 существует единственное обратное комплексное число
существует единственное обратное комплексное число 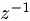 , т.е. число, для которого выполняется равенство
, т.е. число, для которого выполняется равенство 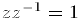 . Для этого умножим обе части последнего равенства на сопряженное к z комплексное число z. В результате получим:
. Для этого умножим обе части последнего равенства на сопряженное к z комплексное число z. В результате получим:
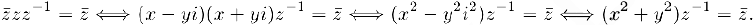
Так как 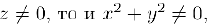 , следовательно.
, следовательно.
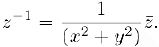
Частным от деления числа 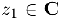 на число
на число 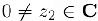 называется комплексное число
называется комплексное число
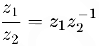
Учитывая приведенное выше представление для обратного комплексного числа, мы можем записать также следующую формулу для вычисления частного:
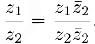
Целая степень комплексного числа определяется точно также, как и целая степень действительного числа.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
