Оглавление:
Рассмотрим функцию 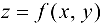 . Ее графиком является некоторая поверхность
. Ее графиком является некоторая поверхность 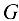 .
.
Определение 20.1. Касательной плоскостью к поверхности 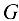 в данной точке
в данной точке 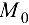 называется плоскость, которая содержит все касательные к кривым, проведенным на поверхности через эту точку.
называется плоскость, которая содержит все касательные к кривым, проведенным на поверхности через эту точку.
Получим уравнение касательной плоскости к поверхности 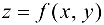 в точке
в точке 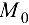 . Рассмотрим сечения поверхности
. Рассмотрим сечения поверхности 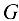 плоскостями
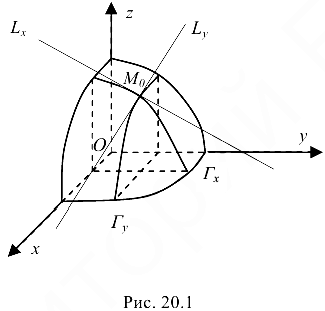
плоскостями 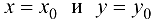 (рис. 20.1). Линия пересечения
(рис. 20.1). Линия пересечения 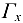 поверхности
поверхности 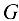 с плоскостью
с плоскостью 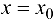 будет определяться системой
будет определяться системой 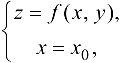 линия пересечения
линия пересечения 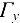 поверхности
поверхности 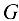 с плоскостью
с плоскостью 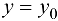 будет определяться системой
будет определяться системой 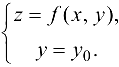
Уравнения касательных прямых 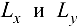 к линиям
к линиям 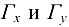 в точке
в точке 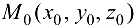 можно представить через пересечение плоскостей соответственно
можно представить через пересечение плоскостей соответственно
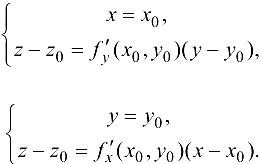
Уравнение плоскости по точке 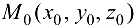 и вектору нормали
и вектору нормали 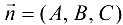 имеет вид
имеет вид 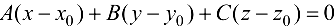 , откуда при
, откуда при 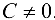 .
.
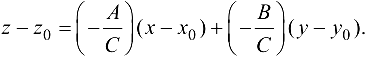
Касательные прямые 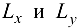 к линиям
к линиям 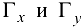 . получаются сечением плоскости (формула (20.3)) двумя плоскостями
. получаются сечением плоскости (формула (20.3)) двумя плоскостями 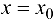 и
и 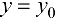 — Следовательно, уравнения касательной прямой
— Следовательно, уравнения касательной прямой 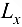 . имеют вид
. имеют вид
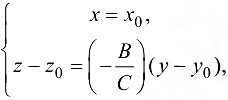
уравнения касательной прямой 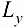 имеют вид
имеют вид
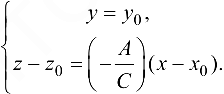
Сравнивая коэффициенты при 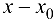 в формулах (20.2) и (20.5), при
в формулах (20.2) и (20.5), при 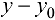 в формулах (20.1) и (20.4), получим
в формулах (20.1) и (20.4), получим
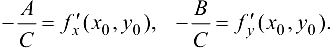
Подставим эти значения в уравнение (20.3), преобразуем и получим уравнение касательной плоскости Р, проходящей через касательные прямые 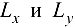 :
:
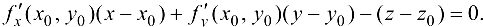
В случае неявного задания поверхности 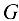 уравнением
уравнением 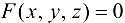 , так как
, так как
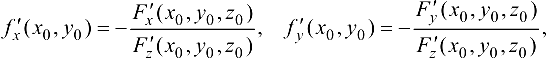
уравнение касательной плоскости Р, проходящей через касательные прямые 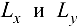 , принимает вид
, принимает вид
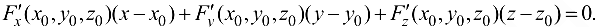
Заметим, что точка, в которой хотя бы одна из частных производных 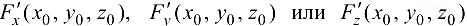 не существует или обращается в пуль, называется особой точкой поверхности. В такой точке поверхность может не иметь касательной плоскости.
не существует или обращается в пуль, называется особой точкой поверхности. В такой точке поверхность может не иметь касательной плоскости.
Определение 20.2. Нормалью к поверхности 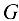 в точке называется прямая, проходящая через эту точку перпендикулярно к касательной плоскости, проведенной в данной точке поверхности.
в точке называется прямая, проходящая через эту точку перпендикулярно к касательной плоскости, проведенной в данной точке поверхности.
Воспользуемся условием перпендикулярности прямой и плоскости и запишем уравнения нормали к поверхности 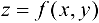 в точке
в точке 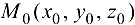 :
:
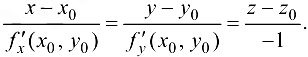
В случае неявного задания поверхности 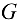 уравнением
уравнением 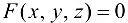 уравнения нормали к поверхности в точке
уравнения нормали к поверхности в точке 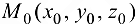 примут вид
примут вид
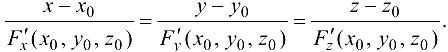
Пример 20.1.
Найти уравнения касательной плоскости и нормали к поверхности 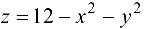 в точке
в точке 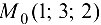 .
.
Решение:
Найдем частные производные функции 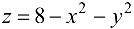 в точке
в точке 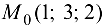 :
:
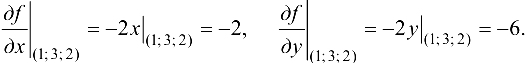
Уравнение касательной плоскости найдем по формуле (20.6):
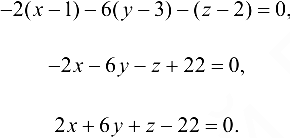
Уравнения нормали найдем по формуле (20.8):
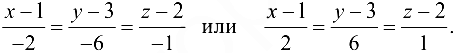
Ответ: 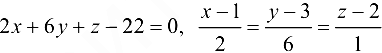 .
.
Пример 20.2.
Найти уравнения касательной плоскости и нормали к поверхности 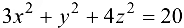 в точке
в точке 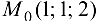 .
.
Решение:
Найдем частные производные функции 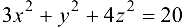 в точке
в точке 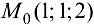 :
:
dF z I z dF о I л PF o ,
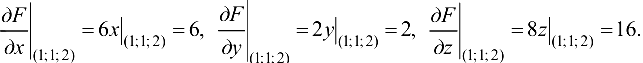
Уравнение касательной плоскости найдем по формуле (20.7):
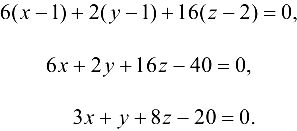
Уравнения нормали найдем по формуле (20.9):
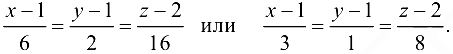
Ответ: 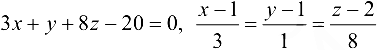 .
.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

