Оглавление:
Интегралы вида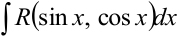 
всегда можно преобразовать к интегралам от рациональной дроби с помощью универсальной тригонометрической подстановки 
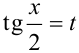. Тогда 
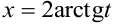, и
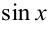Функции 
и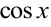 
выражаются через новую переменную 
:
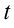Пример:
Найти интеграл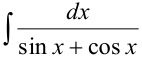 
.
Решение:
Преобразуем интеграл, используя формулы (6.12), (6.13).
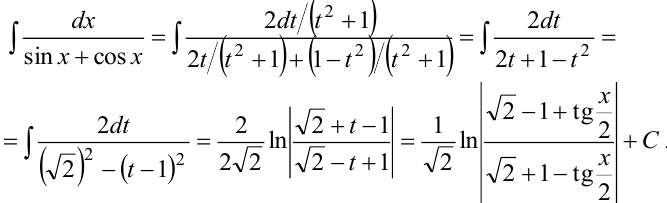
Универсальная тригонометрическая подстановка приводит к сложным рациональным дробям, когда функци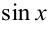и и 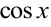присутствуют в степенях выше первой. Поэтому в отдельных частных случаях применяются другие подстановки, которые быстрее приводят к цели.
Частные случаи тригонометрических выражений
1) Интеграл вида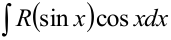 
приводится к виду 
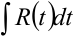подстановкой 
, 
.
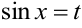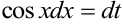2) Интеграл вида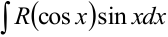 
приводится к виду 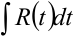подстановкой 
, 
.
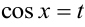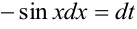3) Интеграл вида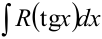 
приводится к виду 
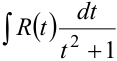подстановкой 
.
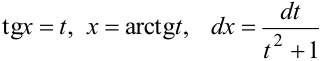4) В интегралах вида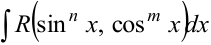 
, где показатели степени 
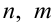— четные, используется подстановка, похожая на универсальную: 
.
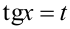Тогда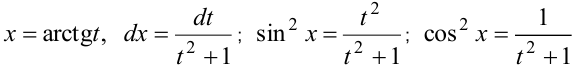 
.
5) Интегралы вида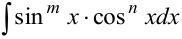 
, где 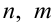— целые числа, положительные или отрицательные.
a) Один из показателей степени — нечетное число, например,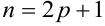 
, где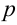 
— целое число. Тогда возможно следующее преобразование:
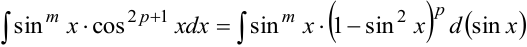. Затем .
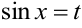b) Показатели степени положительные и четные:
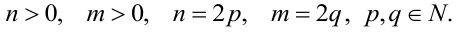
При вычислении интеграла применяются формулы понижения степени
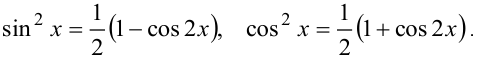
6) Интегралы от произведения тригонометрических функций
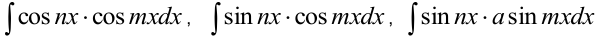
вычисляются с использованием формул, которые преобразуют произведение в сумму.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
