Градиент функции двух переменных
Для анализа направления изменения функции двух переменных в пространстве весьма полезной является векторная характеристика — градиент. Градиентом (или вектор — градиентом) функции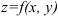 
называется вектор, координатами которого являются частные производные функции:
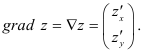
Здесь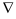 
— обозначение градиента (оператор Гамильтона «набла»}. Градиент функции 
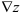в данной точке характеризует направление максимальной скорости изменения функции в этой точке. Зная градиент функции в нескольких точках, можно, по крайней мере, локально, строить линии уровня функции на основе следующей теоремы: пусть задана дифференцируемая функция 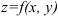и пусть в точке 
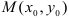величина градиента отлична от нуля. Тогда градиент перпендикулярен линии уровня (точнее, касательной к линии уровня), проходящей через данную точку.
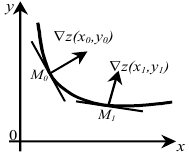
Таким образом, линии уровня можно построить следующим образом. Предположим, мы начинаем с точки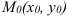 
. Построим в ней градиент. Задаем направление, перпендикулярное градиенту. Оно позволяет построить малую часть линии уровня. Далее рассмотрим близкую точку 
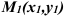и построим градиент в ней. Продолжая этот процесс, можно (с определенной погрешностью) построить линии уровня.
Как и в случае обычных векторов, длину (или модуль) вектора — градиента можно определить в каждой точке по формуле
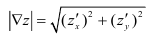
Модуль градиента — величина максимальной скорости изменения функции в данной точке по направлению, показываемому вектором — градиентом.
Остальные темы находится на этой странице и там же можно заказать любые работы по высшей математике:
Обратите внимание на эти страниц, возможно они вам будут полезны:
| Построение прямых. Расстояния |
| Абсолютные экстремумы функции двух переменных |
| Частные производные и дифференциалы |
| Формула трапеций |
