Оглавление:
Задача установления закона распределения функции от случайных величин по заданному закону распределения аргументов является основной.
Общая схема рассуждений здесь следующая. Пусть 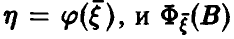 — закон распределения
— закон распределения 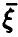 . Тогда очевидно имеем
. Тогда очевидно имеем
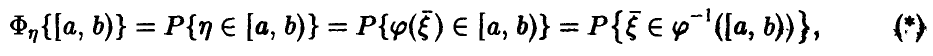
где 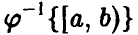 — полный прообраз полуинтервала
— полный прообраз полуинтервала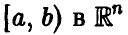 , т.е. совокупность тех значений вектора
, т.е. совокупность тех значений вектора 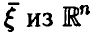 , для которых
, для которых 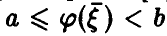 . Последняя вероятность легко может быть найдена, так как закон распределения случайных величин
. Последняя вероятность легко может быть найдена, так как закон распределения случайных величин 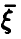 известен
известен
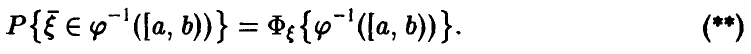
Аналогично, в принципе, может быть найден закон распределения и векторной функции случайных аргументов.
Сложность реализации схемы (*)-(**) зависит только от конкретного вида функции 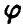 и закона распределения аргументов.
и закона распределения аргументов.
Настоящая глава посвящена реализации схемы (*)-(**) в конкретных, важных для приложений, ситуациях.
Функции одного переменного
Пусть 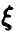 — случайная величина, закон распределения ко-торой задан функцией распределения
— случайная величина, закон распределения ко-торой задан функцией распределения 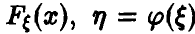 . Если
. Если 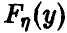 функция распределения случайной величины
функция распределения случайной величины 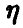 , то приведенные выше соображения дают
, то приведенные выше соображения дают
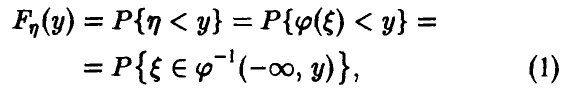
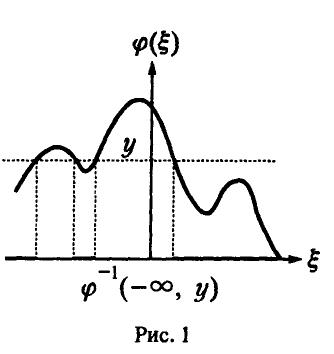
где через 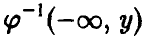 обозначен полный прообраз полупрямой
обозначен полный прообраз полупрямой 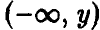 . Соотношение (1) является очевидным следствием (*) и для рассматриваемого случая проиллюстрировано на рис. 1.
. Соотношение (1) является очевидным следствием (*) и для рассматриваемого случая проиллюстрировано на рис. 1.
Монотонное преобразование случайной величины
Пусть 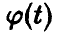 — непрерывная монотонная функция (для определенности — монотонно невозрастающая) и
— непрерывная монотонная функция (для определенности — монотонно невозрастающая) и 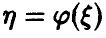 . Для функции распределения
. Для функции распределения 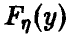 получаем
получаем
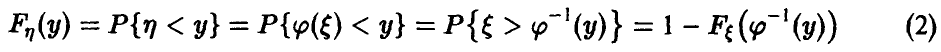
(здесь 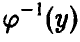 — функция, обратная к
— функция, обратная к 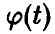 , существование которой обеспечивается монотонностью и непрерывность
, существование которой обеспечивается монотонностью и непрерывность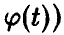 . Для монотонно неубывающей
. Для монотонно неубывающей 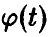 аналогичные выкладки дают
аналогичные выкладки дают

В частности, если 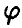 — линейна,
— линейна, 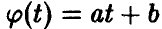 , то при а > 0 (рис. 2)
, то при а > 0 (рис. 2)
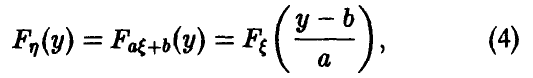
а при а < О
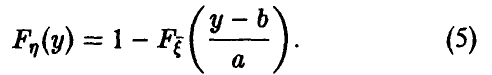
Линейные преобразования не меняют характера распределения, а сказываются лишь на его параметрах.
Линейное преобразование равномерной на [а, b] случайной величины
Пусть 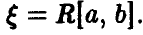 Тогда
Тогда 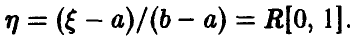
Линейное преобразование нормальной 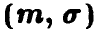 случайной величины
случайной величины
Пусть 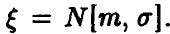 Тогда
Тогда 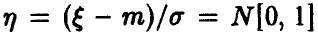 , и вообще, если
, и вообще, если 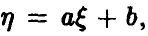 то
то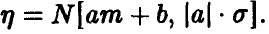
◄ Пусть, например, а > 0. Из (4) заключаем, что
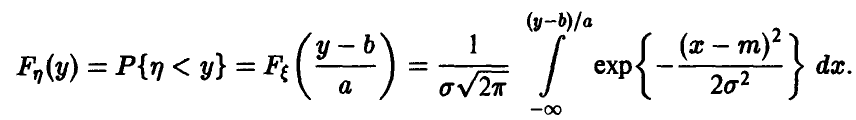
Положим в последнем интеграле u = ах + b. Эта замена дает
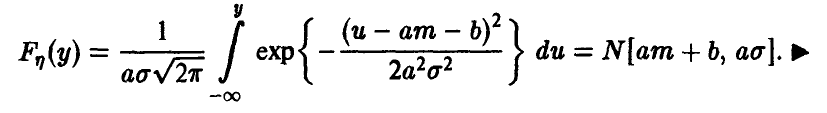
Важное тождество, являющееся источником многих интересных приложений, может быть получено из соотношения (3) при 
Лемма:
Если 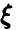 — случайная величина с непрерывной функцией распределения
— случайная величина с непрерывной функцией распределения 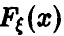 , то случайная величина
, то случайная величина 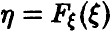 — равномерна на [0, 1].
— равномерна на [0, 1].
 Имеем
Имеем
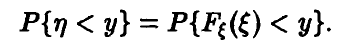
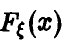 — монотонно не убывает и заключена в пределах от 0 до 1. Поэтому
— монотонно не убывает и заключена в пределах от 0 до 1. Поэтому
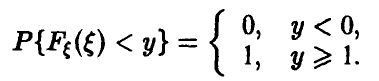
На промежутке же  получаем
получаем
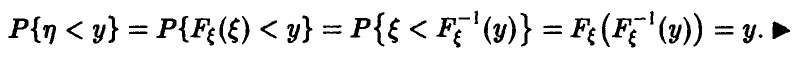
Одним из возможных путей использования доказанной леммы является, например, процедура моделирования случайной величины с произвольным законом распределения 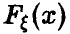 . Как следует из леммы, для этого достаточно уметь получать значения равномерной на [0, 1] случайной величины, тогда значения
. Как следует из леммы, для этого достаточно уметь получать значения равномерной на [0, 1] случайной величины, тогда значения 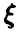 могут быть получены из тождества
могут быть получены из тождества
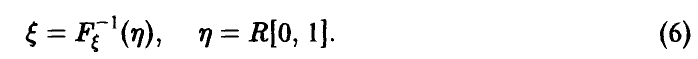
В заключение заметим, что если случайная величина 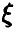 непрерывна и функция
непрерывна и функция 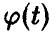 не только монотонна, но и дифференцируема, то
не только монотонна, но и дифференцируема, то 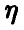 также непрерывна. При этом плотность случайной величины
также непрерывна. При этом плотность случайной величины 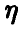 легко может быть получена из (2) или (3):
легко может быть получена из (2) или (3):
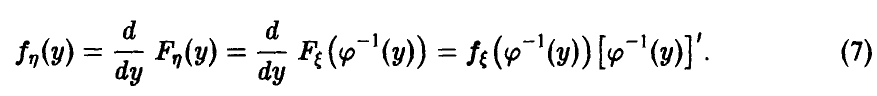
Если 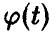 ) свойством монотонности не обладает, то результат может быть получен скрупулезным следованием логике соотношения (1), как показывают приводимые ниже примеры.
) свойством монотонности не обладает, то результат может быть получен скрупулезным следованием логике соотношения (1), как показывают приводимые ниже примеры.
Распределение квадрата равномерной на [—1, 1] случайной величины
Пусть 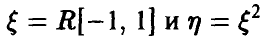 . Рассмотрим (рис. 3)
. Рассмотрим (рис. 3) 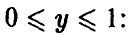
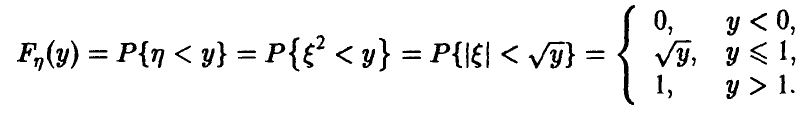
Отсюда для плотности 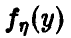 получим
получим
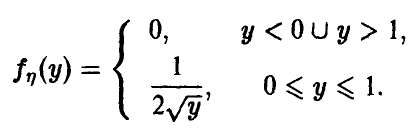
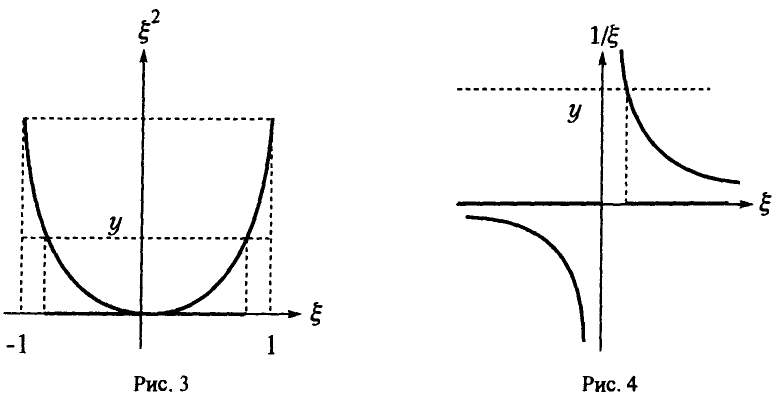
Распределение случайной величины, обратной к случайной величине с распределением Коши
Пусть  — случайная величина, имеющая распределения Коши (см. п. 2.1.1) и
— случайная величина, имеющая распределения Коши (см. п. 2.1.1) и 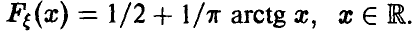 Положим
Положим 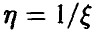 (рис. 4). Следуя (1), получаем:
(рис. 4). Следуя (1), получаем:
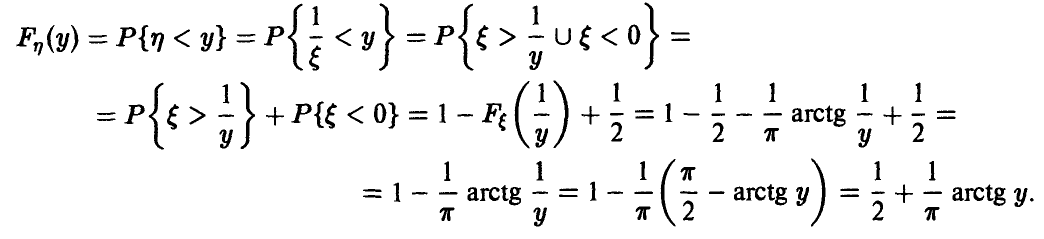
Таким образом, если 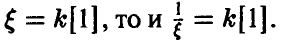
Функции двух переменных. Действия над случайными величинами
Пусть 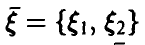 — двумерный случайный вектор с законом распределения
— двумерный случайный вектор с законом распределения 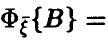
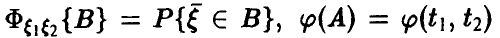 — борелевская функция двух переменных,
— борелевская функция двух переменных, 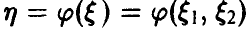 . Как и выше, задачу нахождения закона распределения случайной величины
. Как и выше, задачу нахождения закона распределения случайной величины 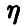 решает схема (*)-(**). В частности, умение решать эту задачу дает возможность производить арифметические действия над случайными величинами: складывать, вычитать, умножать, делить и т. п. Особенно важным для дальнейшего является случай независимых компонент вектора
решает схема (*)-(**). В частности, умение решать эту задачу дает возможность производить арифметические действия над случайными величинами: складывать, вычитать, умножать, делить и т. п. Особенно важным для дальнейшего является случай независимых компонент вектора 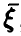 , на котором мы будем всякий раз останавливаться подробнее.
, на котором мы будем всякий раз останавливаться подробнее.
Распределение максимума двух случайных величин
Пусть 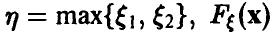 — функция распределения вектора
— функция распределения вектора 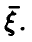
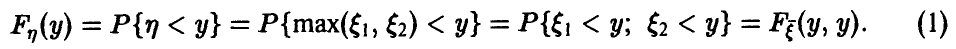
Если вектор 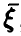 непрерывен и существует плотность распределения
непрерывен и существует плотность распределения 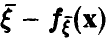 , то
, то 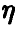 также непрерывна и, очевидно, ее плотность дается соотношением
также непрерывна и, очевидно, ее плотность дается соотношением
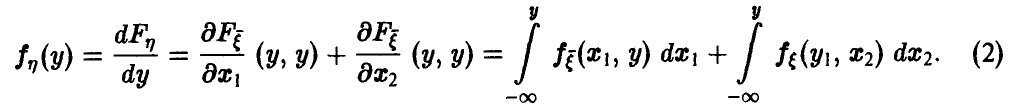
Если дополнительно компоненты 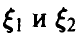 — независимы, то
— независимы, то

а в случае непрерывности
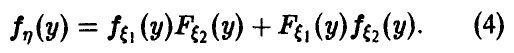
Распределение минимума двух случайных величин
Пусть 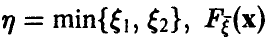 — функция распределения вектора
— функция распределения вектора 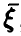 .
.
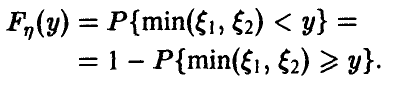
Для последней вероятности получаем (рис. 5).
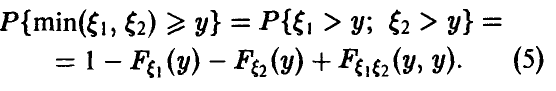
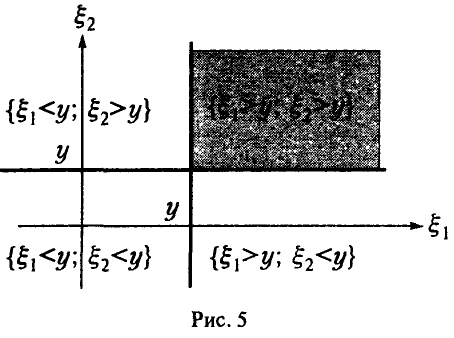
Действительно, из
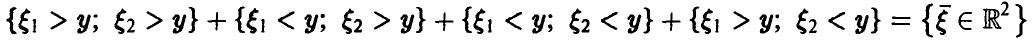
следует
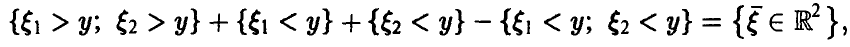
а из последнего легко получается (5).
Окончательно имеем
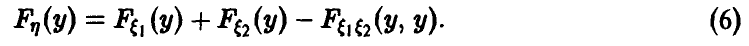
В случае непрерывности  с плотностью
с плотностью 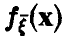 получаем, что
получаем, что  также непрерывна и
также непрерывна и
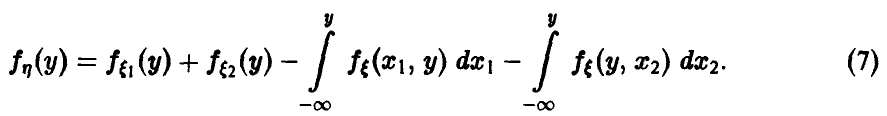
Если  — независимы, то
— независимы, то
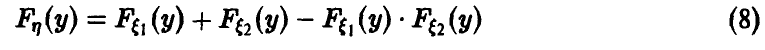
и для непрерывных 
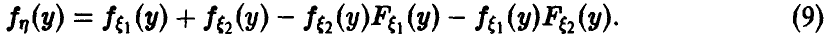
Отметим важную особенность экспоненциального распределения — если 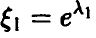 ,
, 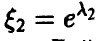 и они независимы, то
и они независимы, то 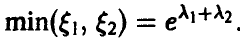
Действительно, (9) дает
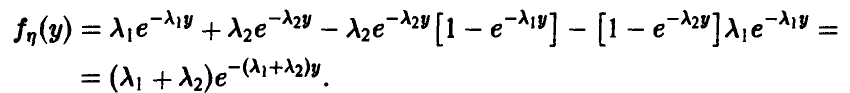
Более того, как будет показано ниже, при достаточно широких предположениях относительно распределения независимых случайных величин 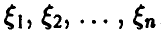 , величина
, величина 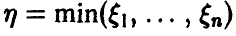 имеет распределение, близкое к экспоненциальному.
имеет распределение, близкое к экспоненциальному.
Сложение случайных величин. Свертка распределений
Пусть 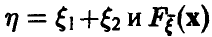 — функция распределения вектора
— функция распределения вектора 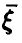 . Для удобства изложения будем предполагать, что
. Для удобства изложения будем предполагать, что 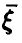 обладает обобщенной плотностью
обладает обобщенной плотностью 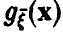 . Тогда получаем
. Тогда получаем
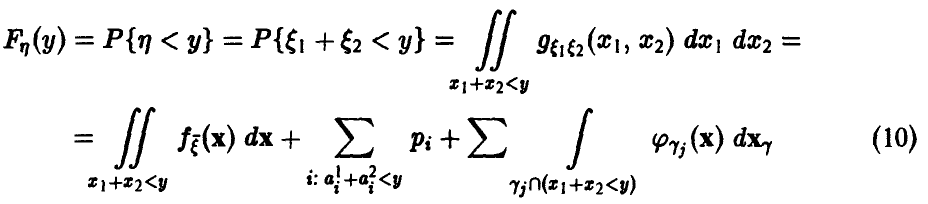
(здесь 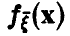 — абсолютно непрерывная составляющая распределения
— абсолютно непрерывная составляющая распределения 
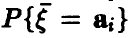 дискретна,
дискретна, 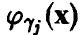 — абсолютно непрерывная составляющая, сосредоточенная на гладкой линии
— абсолютно непрерывная составляющая, сосредоточенная на гладкой линии 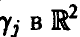 ).
).
В частности, если вектор 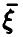 непрерывен, то сумма
непрерывен, то сумма 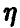 также непрерывна; соотношение (10) записывается в виде
также непрерывна; соотношение (10) записывается в виде
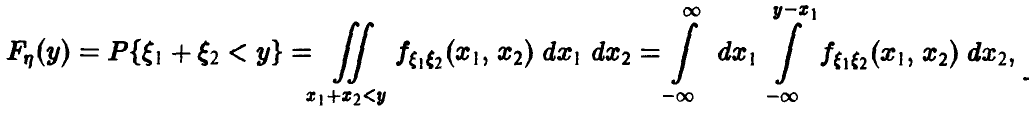
и плотность распределения ц дается соотношением
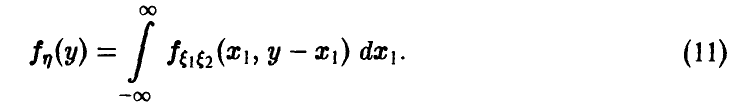
Если  дискретна с рядом распределения
дискретна с рядом распределения 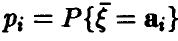 , то сумма также дискретна и
, то сумма также дискретна и
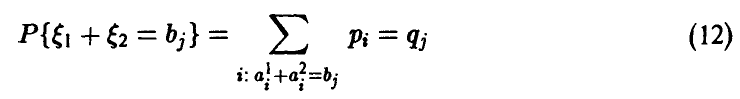
— ее ряд распределения.
Рассмотрим теперь процедуру сложения независимых случайных величин. В этом случае соотношения (10) и (12) приобретают более компактный и завершенный вид.
Пусть ) 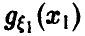 — плотность распределения случайной величины
— плотность распределения случайной величины 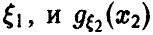 — плотность распределения случайной величины
— плотность распределения случайной величины 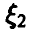
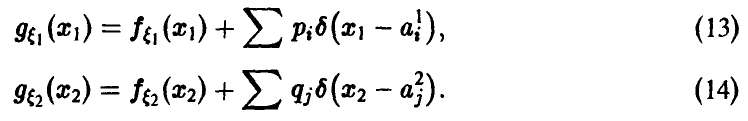
В случае независимости £i и £2 получаем
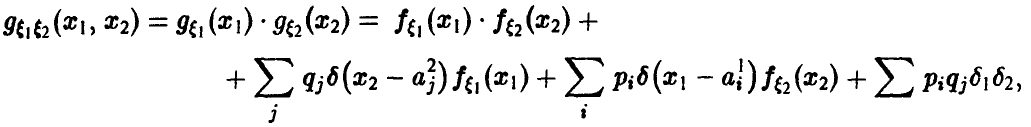
и соотношение (10) можно записать в виде
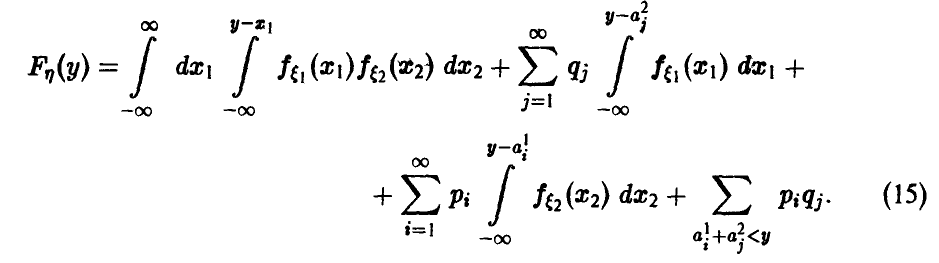
Обобщенная плотность суммы независимых случайных величин дается в этом случае соотношением
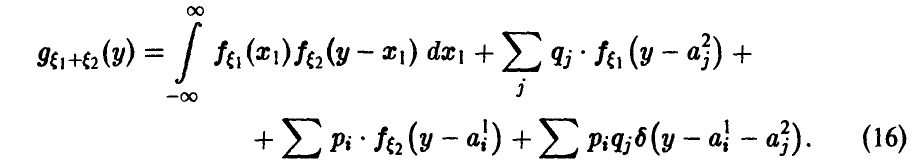
Отметим следующие, важные для приложений, частные случаи соотношений (15) и (16):
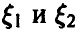 непрерывны и независимы, тогда сумма непрерывна и
непрерывны и независимы, тогда сумма непрерывна и
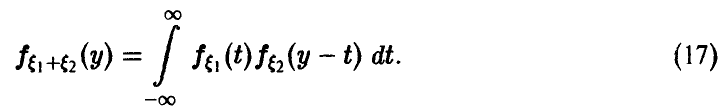
2. 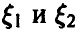 дискретны и независимы, тогда сумма дискретна и
дискретны и независимы, тогда сумма дискретна и
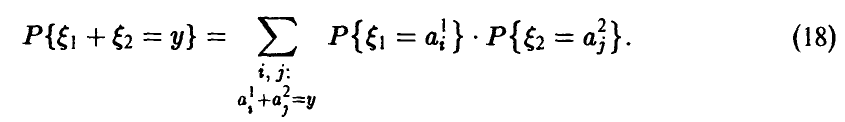
3. 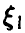 непрерывна,
непрерывна, 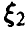 любая
любая
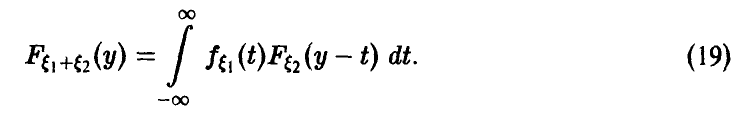
4. 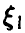 дискретна,
дискретна, 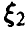 любая
любая
5. 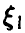 непрерывна,
непрерывна, 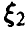 дискретна, в этом случае сумма непрерывна и
дискретна, в этом случае сумма непрерывна и
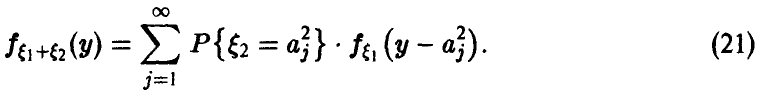
Закон распределения суммы независимых случайных величин называется сверткой законов распределения слагаемых.
Например, соотношение (17) дает формулу свертки плотностей, (18) — свертки рядов распределения, (20) — свертки плотности с рядом распределения. Обычно свертка обозначается знаком «*». Это обозначение дает возможность символически представить функцию распределения суммы независимых слагаемых в виде 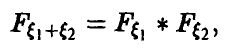
плотность распределения в виде
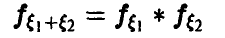
и т. д.
Как правило, при сложении независимых случайных величин характер распределения меняется, даже если складываются одинаково распределенные случайные величины.
Пример:
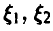 — независимые, равномерные на [0, 1] случайные величины. В соответствии с (15)
— независимые, равномерные на [0, 1] случайные величины. В соответствии с (15)
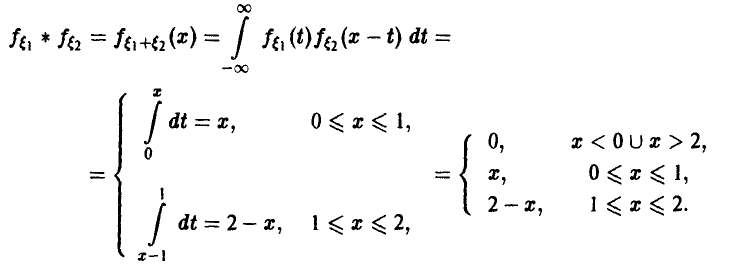
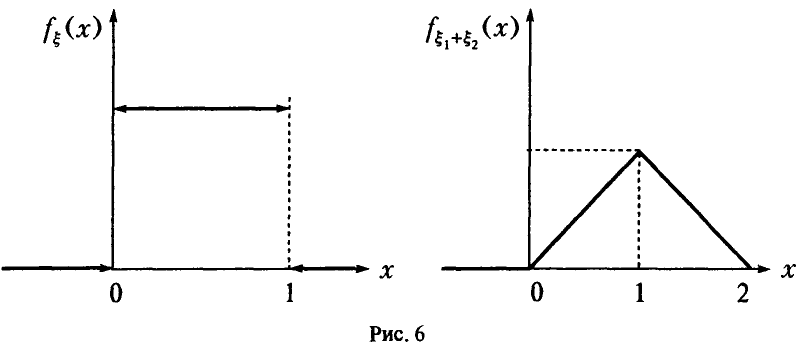
Таким образом, свертка двух равномерных на [0, 1] случайных величин есть «треугольная» случайная величина (рис. 6).
Пример:
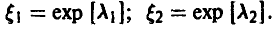 Тогда
Тогда
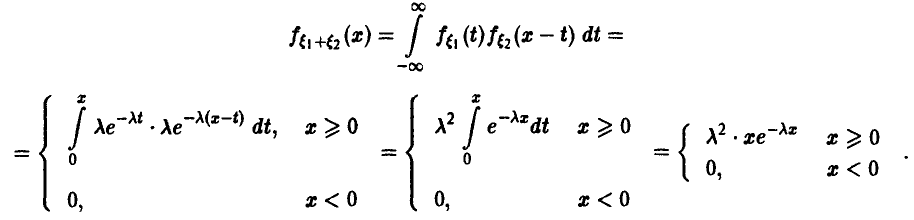
Свертка двух экспоненциальных не является экспоненциальной случайной величиной (рис. 7).
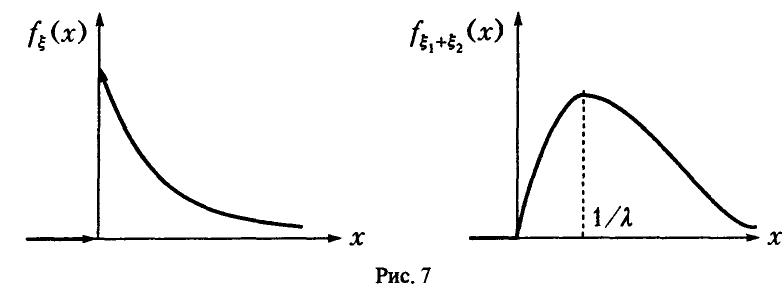
Она является представителем семейства гамма-законов распределения (см. ниже).
Устойчивые относительно свертки распределения играют важную роль в теории и приложениях. Не касаясь вопроса о том, каким условиям должны удовлетворять и как описываются распределения, инвариантные относительно свертки, отметим инвариантность следующих часто встречающихся в приложениях распределений: нормального, пуассонова, гамма-распределения, распределения Коши и распределения Бернулли.
Сформулируем и докажем соответствующие утверждения для нормального распределения, распределения Пуассона и для гамма-распределения.
Теорема:
Если
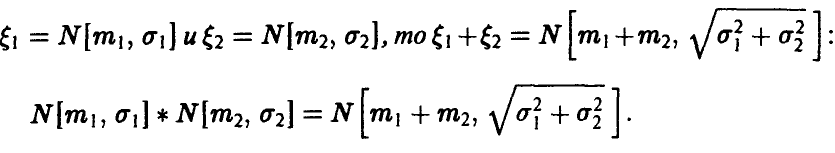
◄ По формуле (15) имеем
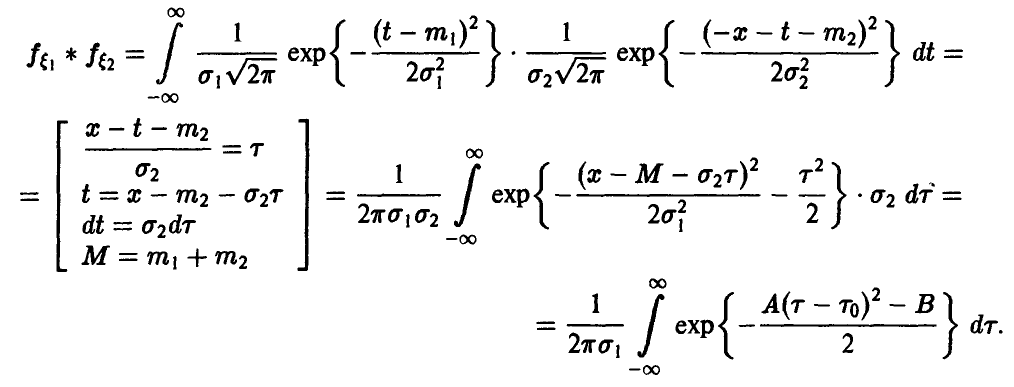
Элементарный (но несколько утомительный) подсчет дает
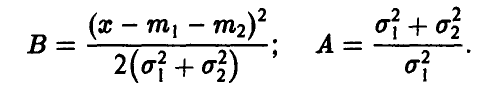
Поэтому
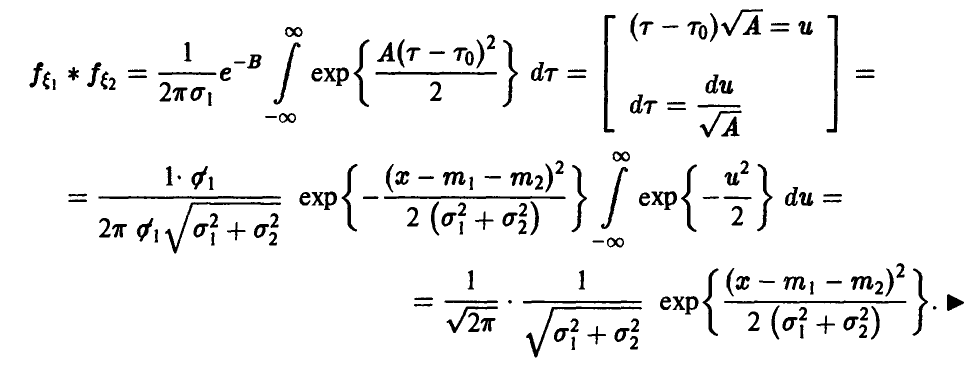
Отметим, что нормальное распределение в некотором смысле «устойчиво» относительно свертки, а именно, если сумма двух независимых случайных величин имеет нормальное распределение, то оказывается слагаемые обязательно нормальны!
Теорема:
Если
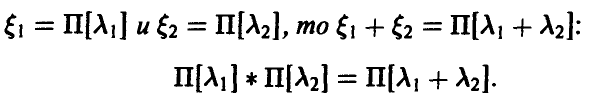
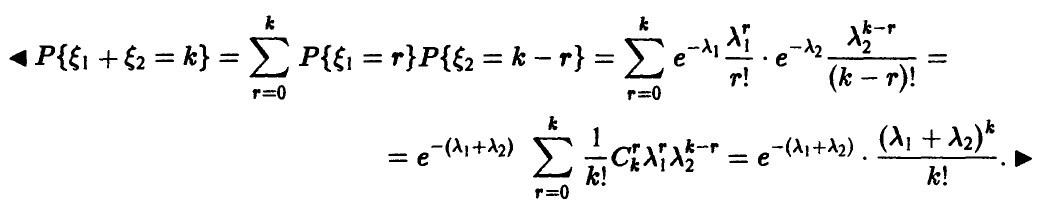
Гамма-плотности
Будем говорить, что случайная величина 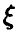 имеет гамма-распределение с параметрами
имеет гамма-распределение с параметрами 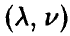 , если ее плотность распределения задается соотношением
, если ее плотность распределения задается соотношением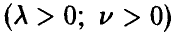
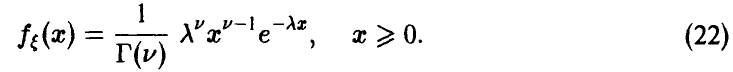
Обозначение: 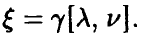
Здесь 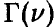 -гамма-функция Эйлера
-гамма-функция Эйлера
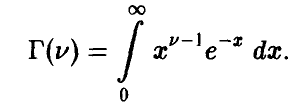
Отметим следующие, хорошо известные свойства гамма-функции:
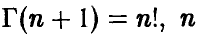 — натуральное.
— натуральное.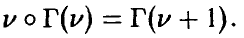
В справедливости этих свойств легко убедиться, интегрируя (22) по частям.
Определение плотности (22) корректно, так как для любых 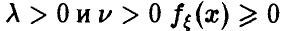 и выполнено условие нормировки
и выполнено условие нормировки
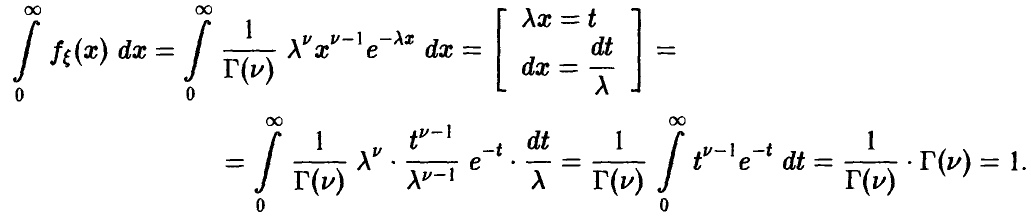
Имеет место теорема.
Теорема:
Если
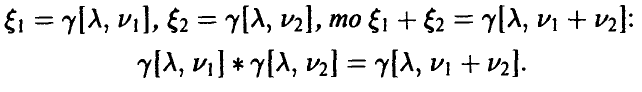
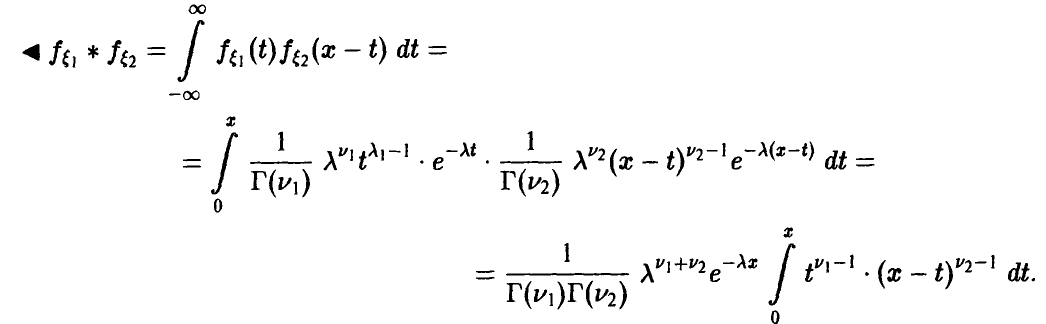
В последнем интеграле положим 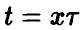 . Тогда
. Тогда
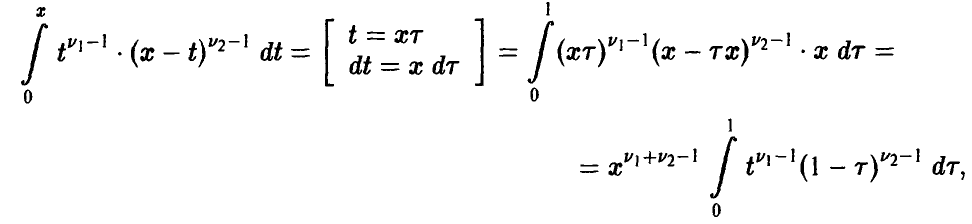
откуда
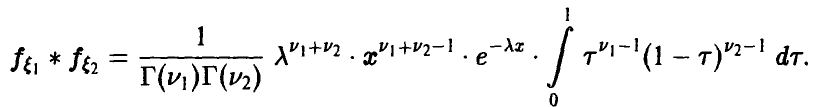
Поскольку 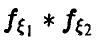 — плотность, то для нее должно быть выполнено условие нормировки, поэтому
— плотность, то для нее должно быть выполнено условие нормировки, поэтому
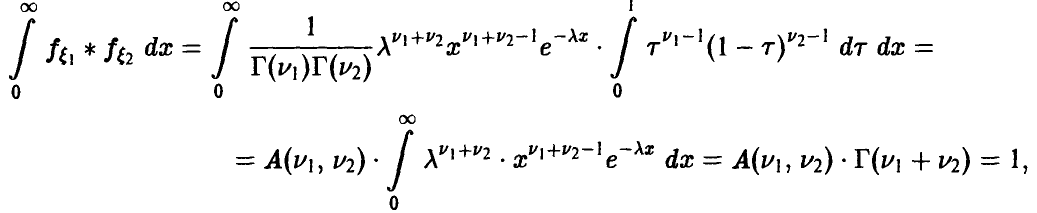
где
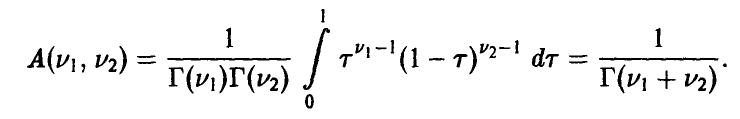
Отсюда окончательно заключаем, что
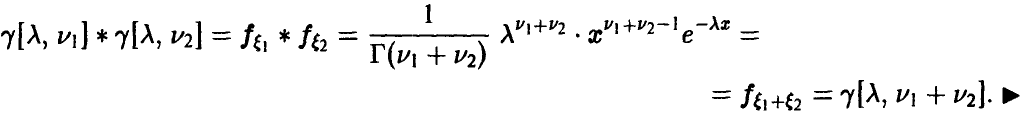
Другие действия над случайными величинами
Задача нахождения закона распределения результата других арифметических действий над случайными величинами решается аналогично. Отметим здесь основные соотношения для случая независимых операндов, следующие из (*)-(**).
Вычитание
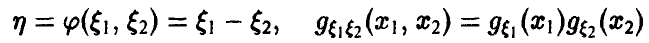
(см. соотношения (13)—(14)).
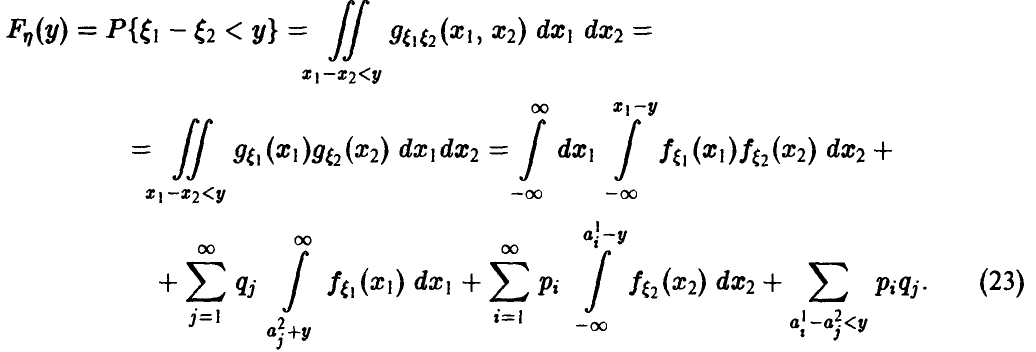
Обобщенная плотность разности 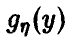 при этом имеет вид
при этом имеет вид
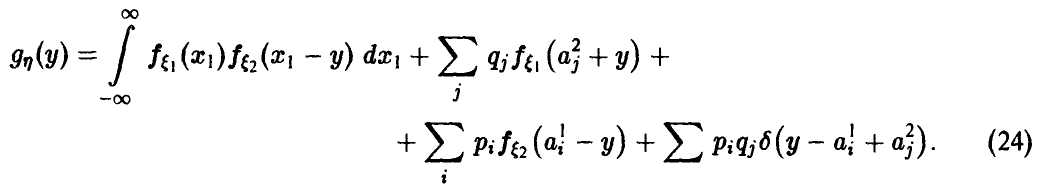
Частные случаи (24), соответственно, для непрерывных
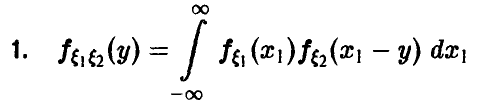
и дискретных случайных величин
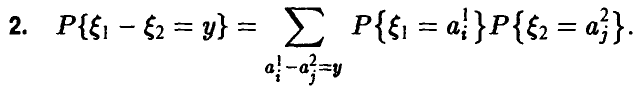
Аналоги соотношений (19), (20) и (21) очевидны.
Умножение
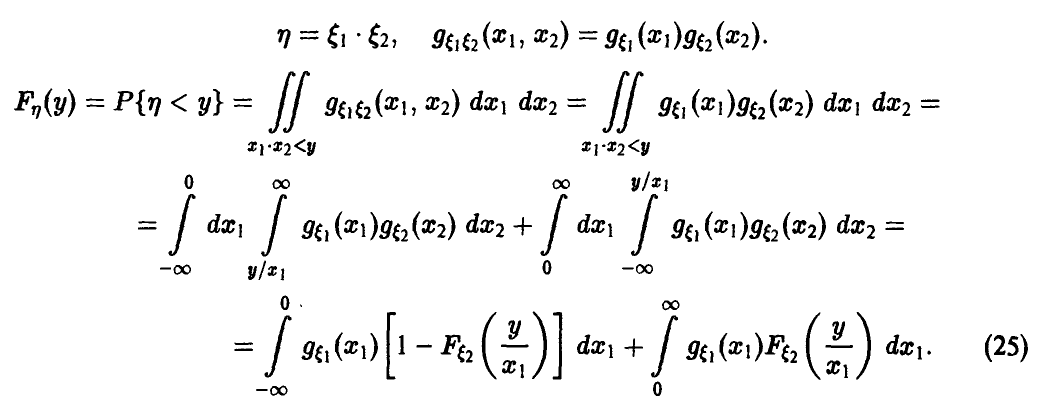
Выражение для обобщенной плотности произведения
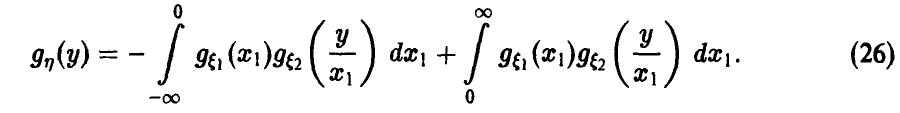
Аналоги соотношений (17)-(21) очевидны.
Деление
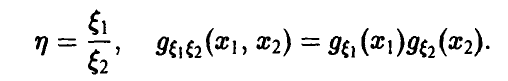
Будем дополнительно предполагать, что 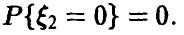
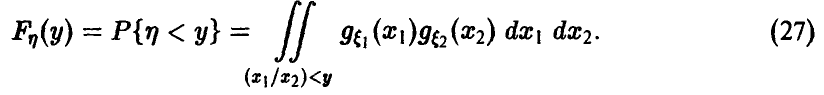
Аналогично для у > 0 имеем
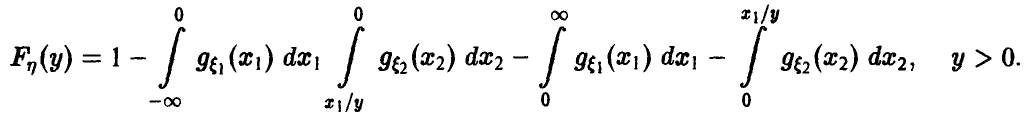
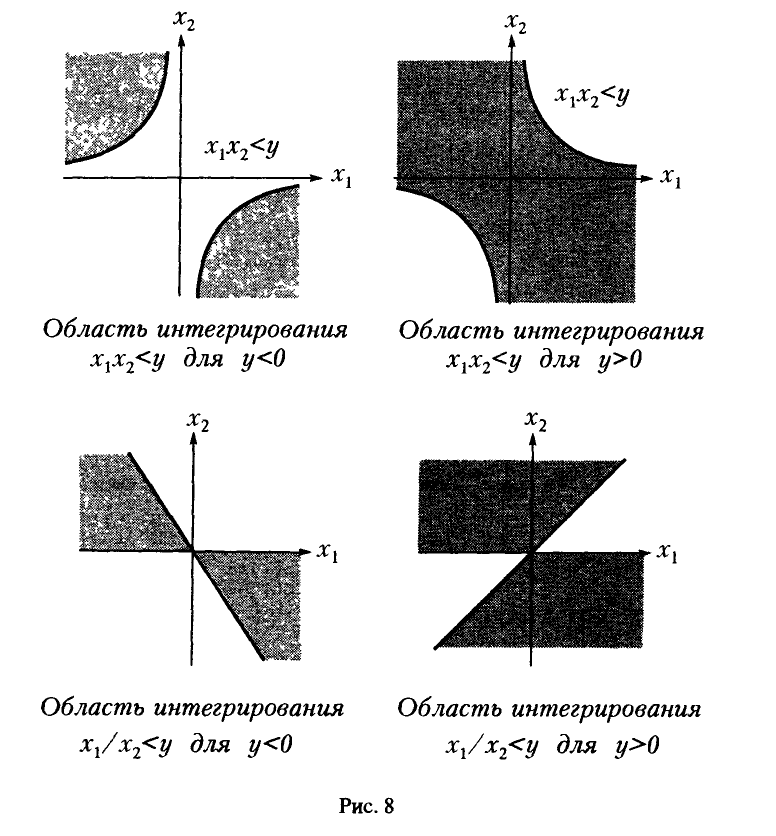
Для дальнейшего нам понадобится выражение функции и плотности распределения частного в предположении, что знаменатель неотрицателен: 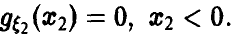
Учитывая вид области интегрирования (рис. 8, 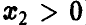 , удобно в (27) расставить пределы интегрирования так, чтобы внешне интегрирование велось по
, удобно в (27) расставить пределы интегрирования так, чтобы внешне интегрирование велось по 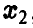 , а внутренне
, а внутренне 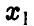
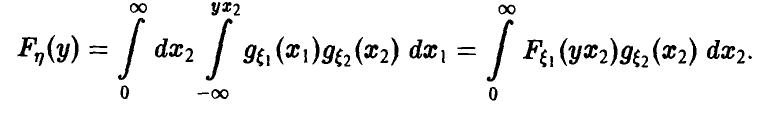
Обобщенная плотность при этом дается равенством
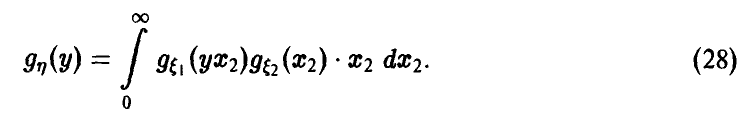
Функции нескольких переменных
В этом разделе мы остановимся на некоторых специфических функциях п переменных и их законах распределения, часто встречающихся в приложениях и играющих важную роль в статистике.
Экстремумы и порядковые статистики
Распределение максимума n случайных величин
Очевидное обобщение рассуждений предыдущего пункта (см. (1)) дает: если 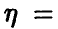
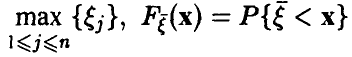 — функция распределения
— функция распределения 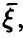 то
то
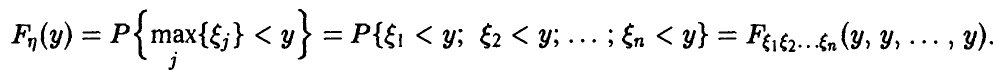
Если вектор 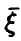 непрерывен с плотностью
непрерывен с плотностью 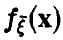 , то плотность
, то плотность 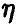 дается соотношением
дается соотношением
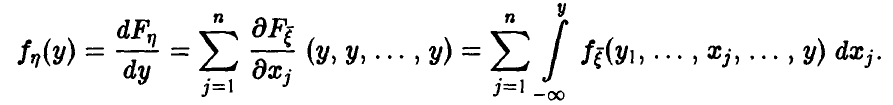
В случае независимости компонент вектора 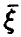 в совокупности
в совокупности

а в предположении непрерывности 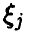
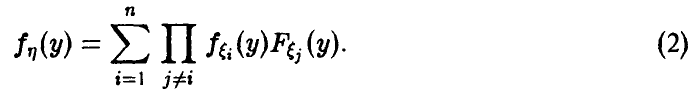
Распределение минимума n случайных величин
Обобщая соотношение (8) дословным повторением выкладок, получаем для вектора 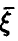 с независимыми в совокупности компонентами
с независимыми в совокупности компонентами
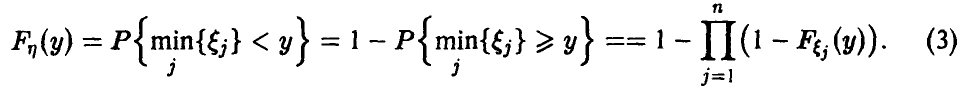
Для непрерывных 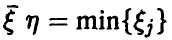 также непрерывна и
также непрерывна и
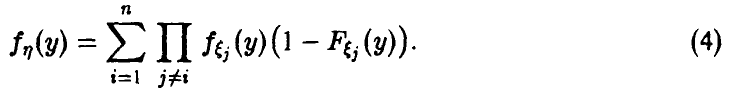
Заметим, что здесь, как и для случая двухкомпонентного вектора  , из условия экспоненциальное компонент следует экспоненциальное минимума.
, из условия экспоненциальное компонент следует экспоненциальное минимума.
Если n достаточно велико, то оказывается, что этот результат — экспоненциальное минимума — слабо зависит от характера распределения компонент. Точнее, имеет место следующее утверждение.
Теорема:
Пусть случайные величины 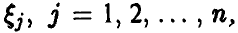 — независимы в совокупности, непрерывны на
— независимы в совокупности, непрерывны на 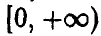 и одинаково распределены. Тогда при
и одинаково распределены. Тогда при  распределение минимума
распределение минимума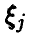 близко к экспоненциальному:
близко к экспоненциальному:
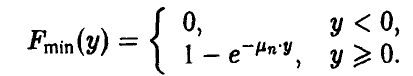
Здесь 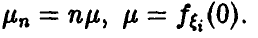
◄ Соотношение (3) в условиях теоремы дает
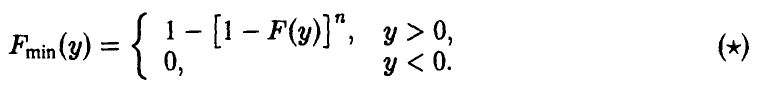
В силу непрерывности  , в окрестности нуля (точнее, в правой полуокрестности) выполняется равенство
, в окрестности нуля (точнее, в правой полуокрестности) выполняется равенство
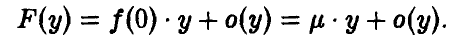
Из соотношения (*) ясно, что при 
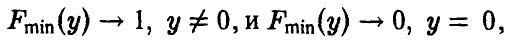 т. е. вся информация о поведении минимума сосредоточена в окрестности нуля. Положим
т. е. вся информация о поведении минимума сосредоточена в окрестности нуля. Положим 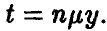 Тогда
Тогда
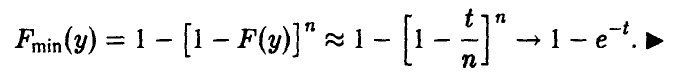
Указанное обстоятельство является теоретическим осмыслением т. н. «принципа слабого звена», широко используемого в теории надежности — надежность агрегата, функционирование которого необходимо зависит от надежности большого количества составляющих, определяется надежностью самого ненадежного из них и описывается экспоненциальным распределением.
Распределение порядковых статистик
Пусть 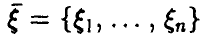 — случайный вектор с законом распределения
— случайный вектор с законом распределения 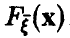 . Вектор
. Вектор 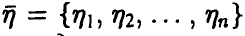 назовем вектором порядковых статистик, а его компоненты —
назовем вектором порядковых статистик, а его компоненты —
порядковыми статистиками, если 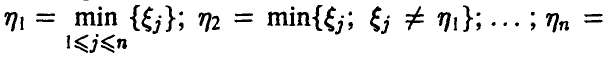
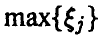 Компоненты вектора
Компоненты вектора 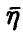 расположены в порядке неубывания
расположены в порядке неубывания
Найдем закон распределения m-й компоненты 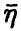 в предположении независимости и одинаковой распределенности компонент
в предположении независимости и одинаковой распределенности компонент 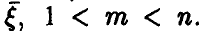 Логику рассуждений рассмотрим на примере n = 3, m = 2.
Логику рассуждений рассмотрим на примере n = 3, m = 2.
Для того, чтобы вторая порядковая статистика приняла значение, меньшее у, нужно чтобы не менее двух из трех компонент вектора 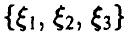 приняли значения, меньшие у. Это значит, что
приняли значения, меньшие у. Это значит, что
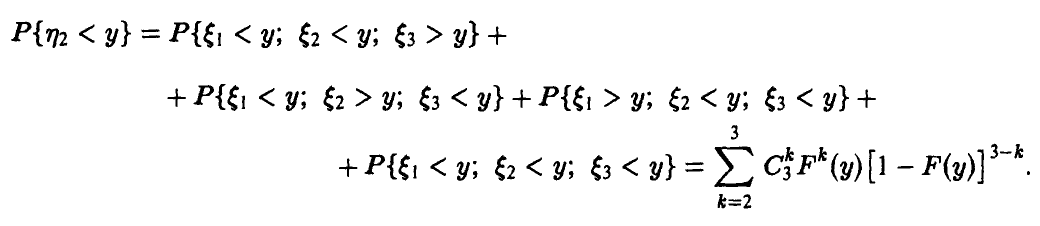
Аналогично для произвольных m и n
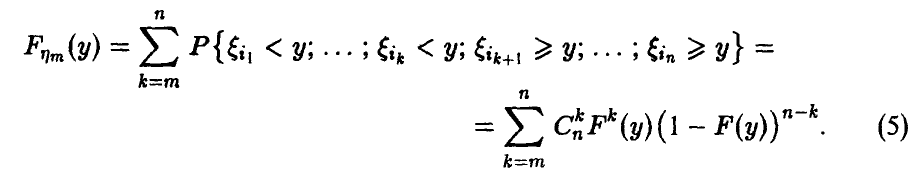
Кратные свертки. Некоторые специальные распределения
Столь же очевидно обобщается на случай произвольного конечного числа слагаемых понятие свертки случайных величин
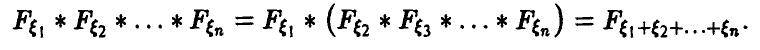
Общие формулы при этом уже достаточно громоздки и необозримы, если только сворачиваемые распределения не являются устойчивыми относительно свертки — в последнем случае ситуация в техническом плане не сложнее, чем в случае двух переменных.
Особо отметим, что для нормальных, независимых в совокупности случайных величин из свойств линейного преобразования и теоремы 1 следует, что, если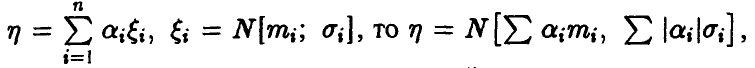 т. е. линейная комби нация независимых нормальных случайных величин является нормальной случайной величиной.
т. е. линейная комби нация независимых нормальных случайных величин является нормальной случайной величиной.
Распределение 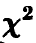 — Пирсона
— Пирсона
Пусть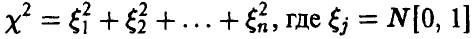 независимы в совокупности.
независимы в совокупности.
Распределение суммы квадратов п независимых нормальных с параметрами (0, 1) случайных величин называется 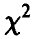 —распределением Пирсона с n степенями свободы.
—распределением Пирсона с n степенями свободы.
Читается — хи-квадрат. Обозначение: 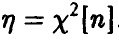 . Устойчивость
. Устойчивость 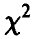 -распределения относительно свертки усматривается непосредственно из определения
-распределения относительно свертки усматривается непосредственно из определения
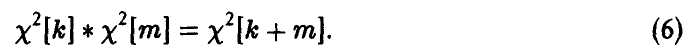
Для нахождения закона распределения случайной величины 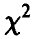 , заметим, что если
, заметим, что если 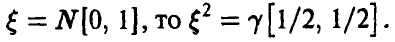
◄ Действительно,
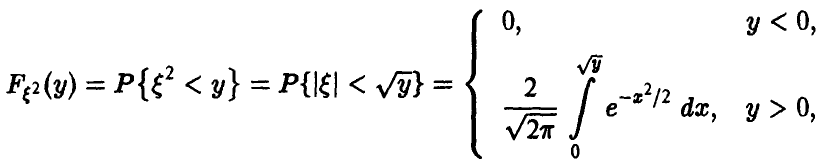
откуда
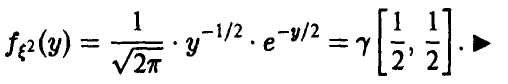
В силу устойчивости гамма-распределения относительно свертки получаем
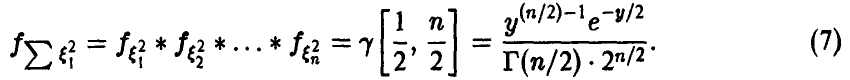
t-распределение Стьюдента
Пусть 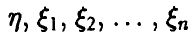 — независимые нормальные с параметрами (0, 1) случайные величины и пусть
— независимые нормальные с параметрами (0, 1) случайные величины и пусть

Распределение случайной величины t называется распределением Стьюдента с n степенями свободы.
Обозначение: t = t[n].
Найдем выражение для закона распределения t[n]. Отметим, что числитель рассматриваемого отношения нормален с параметрами 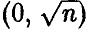 , а знаменатель неотрицателен и его распределение дается выражением
, а знаменатель неотрицателен и его распределение дается выражением
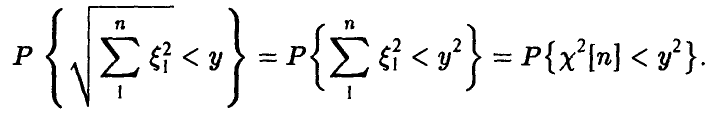
Из (7) заключаем, что
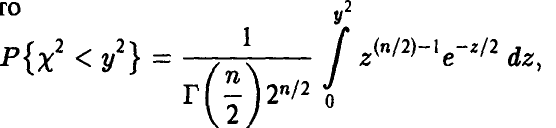
отсюда для плотности 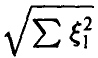 имеем
имеем
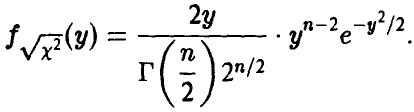
Поэтому для частного t[n], следуя (28), получаем
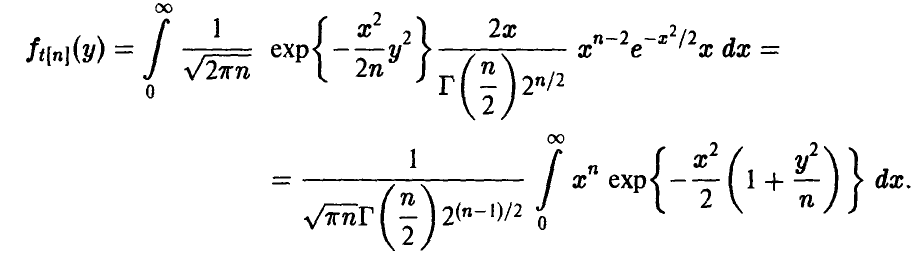
Делая в последнем интеграле замену
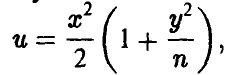
приходим к формуле
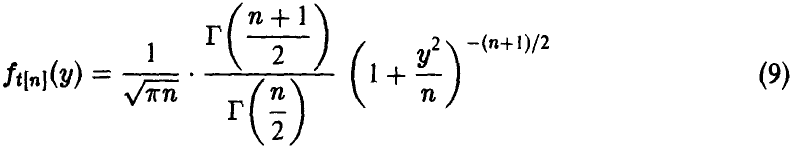
Заметим, что при 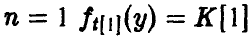 — плотность распределения Коши.
— плотность распределения Коши.
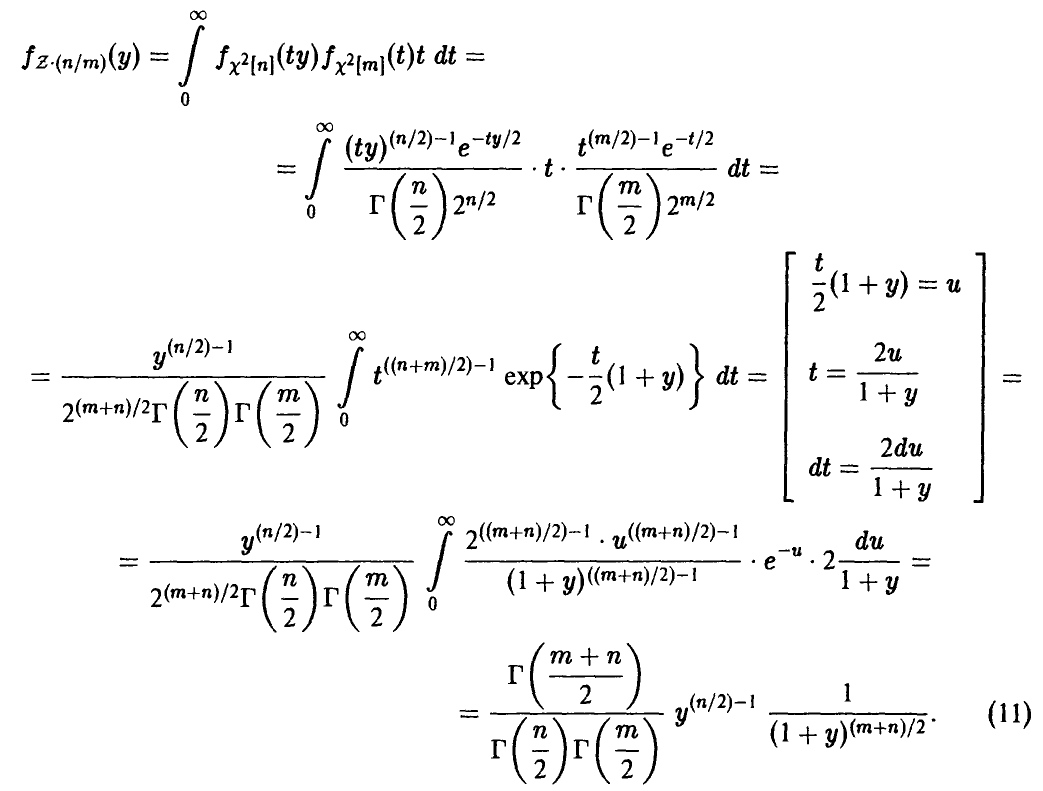
Z -распределение Фишера
Пусть 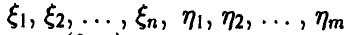 — независимые в совокупности нормальные с параметрами (0, 1) случайные величины. Положим
— независимые в совокупности нормальные с параметрами (0, 1) случайные величины. Положим
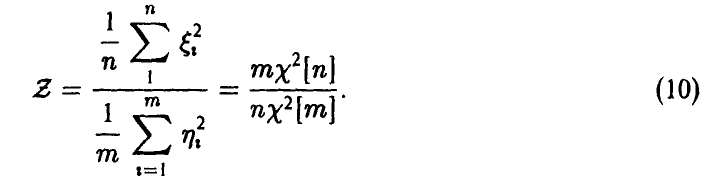
Величина Z называется случайной величиной Фишера-Снедекора. Обозначение Z = Z[n, m].
Закон распределения случайной величины Z найдем, используя (28) и (7). Имеем
Из соотношения (4) для линейного преобразования 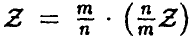 окончательно получаем
окончательно получаем
Многомерное нормальное распределение
Пусть 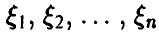 — независимые в совокупности нормальные с параметрами (0, 1) случайные величины,
— независимые в совокупности нормальные с параметрами (0, 1) случайные величины, 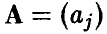 — невырожденная матрица порядка
— невырожденная матрица порядка 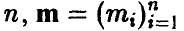 — столбец. Рассмотрим случайный вектор
— столбец. Рассмотрим случайный вектор 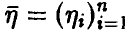 , задаваемый соотношением
, задаваемый соотношением

Отметим, что каждая компонента 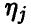 является линейной комбинацией нормальных с параметрами (О, 1) случайных величин
является линейной комбинацией нормальных с параметрами (О, 1) случайных величин
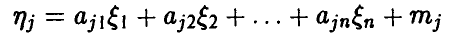
и, в силу сделанного выше замечания, является нормальной случайной величиной.
Найдем закон распределения вектора (13). Пусть 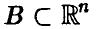 — борелевское, тогда
— борелевское, тогда
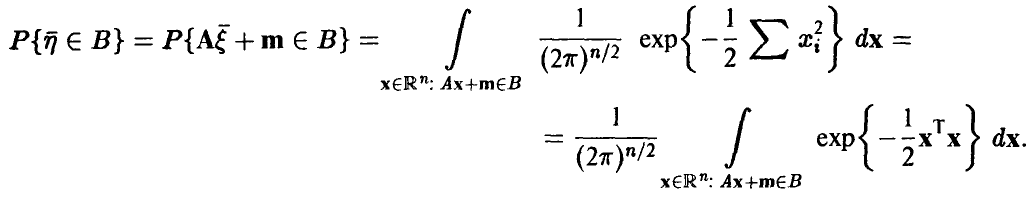
Сделаем в последнем интеграле замену переменных, положив
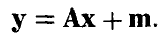
В силу невырожденности А эта замена невырождена и ее якобиан равен 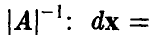
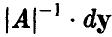 Получим
Получим
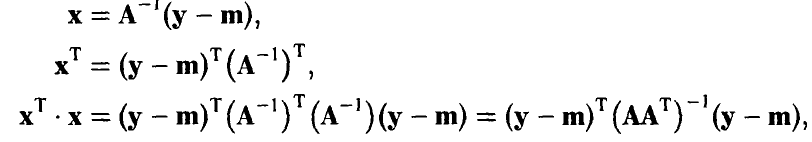
поэтому для любого борелевского  имеем
имеем
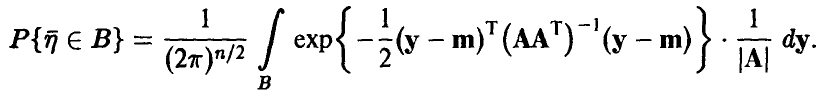
Положим 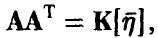 тогда
тогда 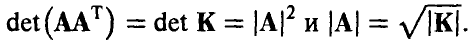
Для закона распределения вектора 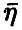 получим
получим
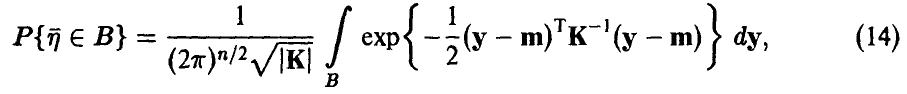
отсюда следует, что 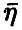 — непрерывный вектор, плотность которого дается равенством
— непрерывный вектор, плотность которого дается равенством
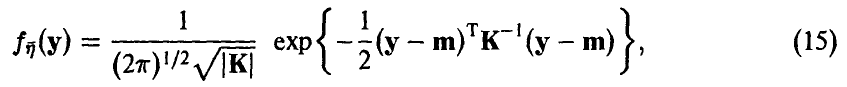
т. е. полностью определяется матрицей К и вектором m.
Распределение (14)-(15) называется невырожденным нормальным п-мерным распределением с параметрами (К, m). Обозначение 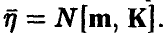
Отметим, что здесь К — симметричная, положительно определенная матрица, 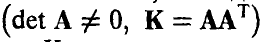 , m — произвольный вектор из
, m — произвольный вектор из 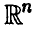
Компоненты нормального случайного вектора — нормальные случайные величины. Однако нормальности компонент недостаточно для того, чтобы вектор был нормальным в смысле определения, данного выше.
Пример:
Пусть 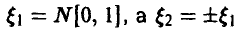 с равными вероятностями
с равными вероятностями
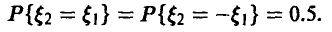
◄ Компонента 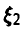 нормальна с параметрами (0, 1), что немедленно следует из выкладок
нормальна с параметрами (0, 1), что немедленно следует из выкладок
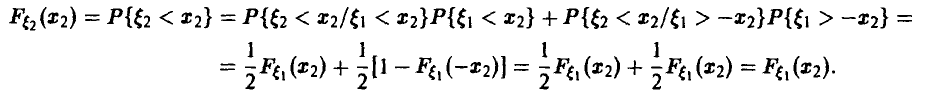
В то же время, совместное распределение  сосредоточено на паре прямых
сосредоточено на паре прямых  , так что обобщенная плотность распределения этого вектора может быть представлена в виде
, так что обобщенная плотность распределения этого вектора может быть представлена в виде
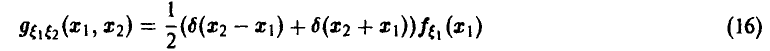
и не является плотностью совместного нормального распределения (15). ►
Отметим еще одно важное свойство компонент нормального вектора: они независимы тогда и только тогда, когда матрица К — диагонально.
◄ Действительно, если 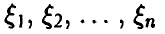 независимы и нормальны
независимы и нормальны 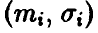 , то для совместной плотности получаем
, то для совместной плотности получаем
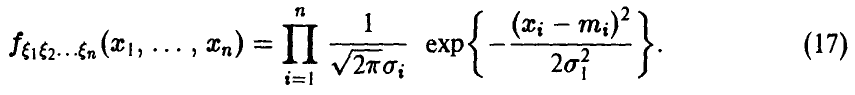
Легко убедиться в том, что плотность (17).имеет вид (15) с 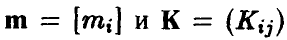
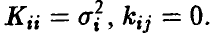
Обратно, пусть 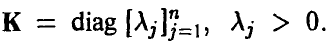 Тогда
Тогда 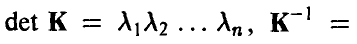
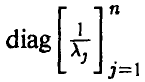 и плотность (15) принимает вид
и плотность (15) принимает вид
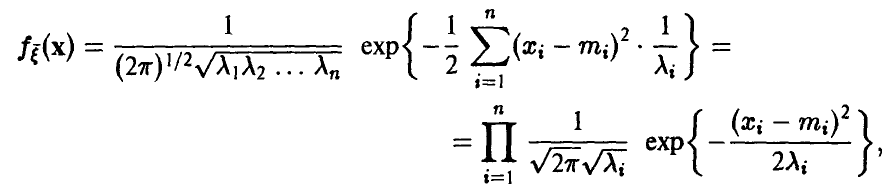
т. е. представима в виде произведения нормальных плотностей, каждая из которых является индивидуальной плотностью распределения г-й компоненты, что и означает независимость компонент  . ►
. ►
Пусть теперь 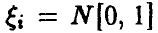 — независимые, А — m х n-матрица, ранг которой rang А = r. Можно показать, что вектор
— независимые, А — m х n-матрица, ранг которой rang А = r. Можно показать, что вектор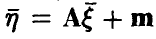 имеет r-мерное нормальное распределение, которое в случае r = m является невырожденным в
имеет r-мерное нормальное распределение, которое в случае r = m является невырожденным в 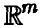 с параметрами
с параметрами 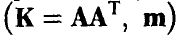 , в случае же r < m это распределение вырождено в
, в случае же r < m это распределение вырождено в 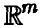 и сосредоточено на некотором подпространстве L, dim L = r.
и сосредоточено на некотором подпространстве L, dim L = r.
Независимость функций независимых аргументов
В заключение этой главы рассмотрим одно важное свойство функций случайных аргументов.
Пусть 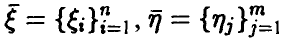 — случайные векторы, законы распределения которых даются, соответственно, функциями
— случайные векторы, законы распределения которых даются, соответственно, функциями 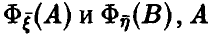 — борелевское из
— борелевское из 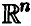 , В — борелевское из
, В — борелевское из 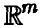 . Пусть
. Пусть — борелевские функции в
— борелевские функции в 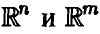 соответственно. Тогда имеет место
соответственно. Тогда имеет место
Теорема:
Если векторы 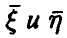 независимы, то случайные величины
независимы, то случайные величины 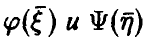 — независимы.
— независимы.
◄ Из независимости векторов 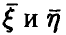 получаем
получаем
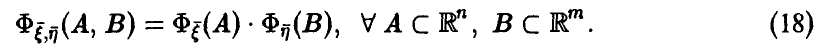
Рассмотрим
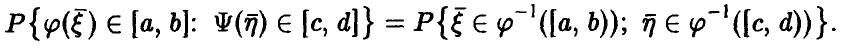
В силу соотношения (18) последняя вероятность представима в виде
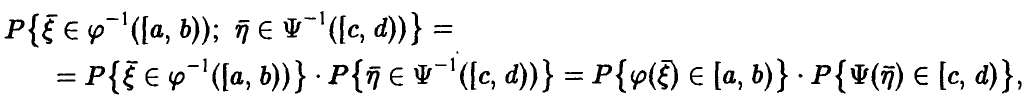
откуда и следует искомое. ►
Функция распределения случайной величины
Функцией распределения случайной величины называют функцию 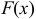 , определяющую вероятность того, что случайная величина
, определяющую вероятность того, что случайная величина 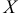 в результате испытания примет значение, меньше
в результате испытания примет значение, меньше 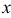 , т.е.
, т.е.
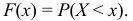
Геометрически 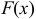 есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки
есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки 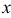 .
.
Иногда вместо термина «Функция распределения» используют термин «Интегральная функция».
Случайную величину называют непрерывной, если её функция распределения есть непрерывная, кусочно — дифференцируемая функция с непрерывной производной.
Свойства функции распределения
1) Значения функции распределения принадлежат отрезку [0, 1]:
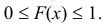
2) 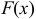 — неубывающая функция, т.е.
— неубывающая функция, т.е. 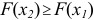 , если
, если 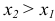 .
.
3) Вероятность того, что случайная величина 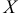 примет значение, заключённое в интервале
примет значение, заключённое в интервале 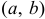 , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале: 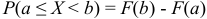 .
.
4) Вероятность того, что непрерывная, случайная величина 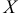 примет одно определённое значение, равна нулю. Тем самым имеет смысл рассматривать вероятность попадания непрерывной случайной величины в интервал, пусть даже сколько угодно малый.
примет одно определённое значение, равна нулю. Тем самым имеет смысл рассматривать вероятность попадания непрерывной случайной величины в интервал, пусть даже сколько угодно малый.
5) Если возможное значение случайной величины 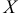 принадлежит интервалу
принадлежит интервалу 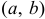 ,то:
,то: 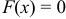 , при
, при 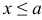 ;
; 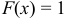 , при
, при 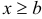 .
.
6) Если возможное значение непрерывной случайной величины расположены на всей оси, то 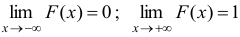 .
.
График функции распределения
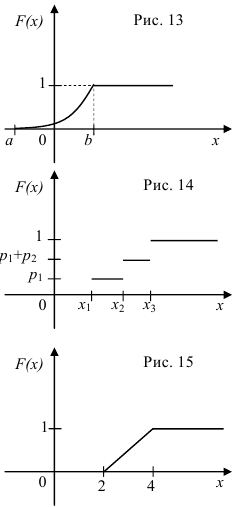
График функции распределения непрерывной случайной величины, возможные значения которой принадлежат интервалу 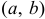 изображен на рис. 13.
изображен на рис. 13.
График функции распределения дискретной случайной величины имеет ступенчатый вид. На рис. 14 изображен график функции распределения дискретной случайной величины 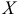 заданной таблицей распределения
заданной таблицей распределения
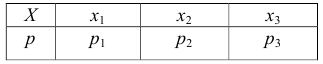
Пример:
Построить график функции
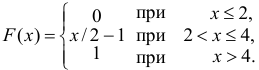
Найти вероятность того, что в результате испытания случайная величина 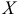 примет значение, заключенное в интервале (2; 3).
примет значение, заключенное в интервале (2; 3).
Решение:
График функции изображен на рис. 15. Вероятность того, что случайная величина 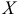 примет значение, заключённое в интервале (2, 3), равна приращению функции распределения на этом интервале:
примет значение, заключённое в интервале (2, 3), равна приращению функции распределения на этом интервале: 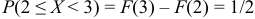 .
.
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:
Решение заданий и задач по предметам:
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность

