Геометрическая вероятность с примерами решения и образцами выполнения

Пусть рассматривается непрерывная вероятностная схема, т.е. пространство элементарных исходов представляет собой некоторую ограниченную область (отрезок, многоугольник, круг, параллелепипед, шар и т. п.) k-мерного пространства (прямой, плоскости, трехмерного пространства и т.д.). Естественно желание обобщить принцип равновероятности элементарных исходов классической вероятности и на эту схему. Однако в непрерывном случае число элементарных исходов бесконечно и, воспользовавшись принципом равновероятности, мы не смогли бы приписать каждому элементарному исходу иной вероятности, кроме нуля. Поэтому подойдем к определению геометрической вероятности по-другому. Рассмотрим сначала отрезок [0, 1] и предположим, что идеальная частица равномерно бросается на этот отрезок. Понятию равномерности придадим следующий смысл. Каждому отрезку 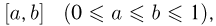Геометрическая вероятность независимо от его расположения, поставим в соответствие одинаковую вероятность попадания частицы на этот отрезок, равную его длине: 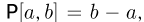а затем эту вероятность попытаемся с помощью трех аксиом 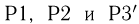Геометрическая вероятность продолжить на любое подмножество точек отрезка [0, 1]. Очевидно, что вероятность попадания частицы в любую точку х равна нулю, вероятность попадания на любой интервал (а, b) или полуинтервал 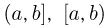Геометрическая вероятность (на отрезке [0, 1]) равна b — а, вероятность попадание в любое множество точек на отрезке [0, 1], состоящее из конечного и даже счетного объединения непересекающихся отрезков, интервалов и полуинтервалов равна сумме их длин, т. е. «длине», или лучше сказать, мере этого множества. В частности, вероятность попадания частицы в множество рациональных точек равна нулю.

Однако, как уже говорилось, имеется препятствие к такому продолжению, связанное с существованием подмножеств, которым разумным образом с сохранением трех аксиом вероятность мы никак не сможем приписать. Поэтому приходится ограничиваться только элементами борелевской 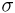Геометрическая вероятность —алгебры 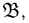порожденной всевозможными интервалами (т.е. подмножествами, имеющими меру), что, впрочем, более чем достаточно для практических потребностей.

В общем случае геометрическая вероятность определяется совершенно аналогично. Пусть 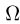некоторая область, имеющая меру 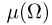(длину, площадь, объем и т.д.), такую, что 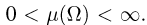Скажем, что точка равномерным образом попадает в 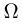Геометрическая вероятность (реализуется принцип геометрической вероятности), если вероятность Р(А) попадания ее в каждую область А, являющуюся подобластью 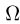, пропорциональна мере этой области 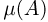Геометрическая вероятность или в силу аксиомы нормированности

Пример:

В круг радиусом 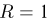Геометрическая вероятность равномерно бросается точка. Найдем вероятность события А, заключающегося в попадании этой точки в круг радиусом 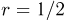с тем же центром (рис. 2).

Рассмотрим два способа решения этой задачи:

1)вероятность Р(А) определяется как отношение площади внутреннего круга к площади внешнего:

2) заметим, что в силу принципа геометрической вероятности как угол 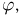Геометрическая вероятность так и расстояние 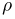от точки 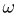до центра О должно быть распределено равномерно. Поскольку точки, равноотстоящие от центра, все либо одновременно принадлежат меньшему кругу, либо нет, то вероятность попадания в этот круг равна отношению радиусов: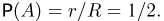 Геометрическая вероятность

Итак, мы получили в одной и той же задаче два разных ответа. Причина кроется в том, что понятие геометрической вероятности не инвариантно относительно преобразований рассматриваемой области 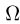Геометрическая вероятность . В частности, в нашем примере при втором способе решения мы считаем, что равновероятно попадание точки в области 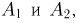заштрихованные на рис. 3. Но с точки зрения обычного понятия площади, используемого при первом способе решения, это не так. Значит, вероятность существенно зависит от способа определения понятия «равновероятно» или, иными словами, от того, как мы задали меру 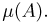Геометрическая вероятность Именно на неинвариантности понятия геометрической вероятности относительно преобразований основаны многочисленные парадоксы, часто приводимые в различных учебниках.

Возвращаясь к рассматриваемому примеру, отметим, что в приведенной постановке задачи предпочтительным нужно считать первый способ. Однако не следует думать, что второе решение относится к числу математических фокусов. Представляемая этим решением модель сигнала с равномерно распределенными фазой (углом) и амплитудой (радиусом) находит широкое применение в статистической радиофизике.

Пример:

На Землю параллельно плоскости экватора падает поток метеоритов. Найдем вероятность того, что упавший метеорит попадет между 15° и 45° северной широты (событие А). Естественно предполагать, что поток метеоритов равномерно распределен на плоскости, перпендикулярной плоскости экватора. Если мы теперь спроецируем земной шар на эту плоскость (рис. 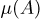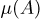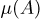4), то получим, что вероятность наступления события А пропорциональна площади Геометрическая вероятность заштрихованной области А. Определим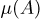

Окончательно получаем

Пример:

Поступление каждого из двух сигналов в приемник равновозможно в любой момент промежутка времени Т. Найдем вероятность того, что приемник будет «забит» (событие А), что происходит в том случае, когда промежуток времени между моментами поступления обоих сигналов меньше 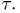Геометрическая вероятность Для этого обозначим моменты поступления сигналов через х и у. Ясно, что для наложения сигналов необходимо и достаточно, чтобы 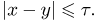Изобразим х и у как точки внутри квадрата со сторонами Т (рис.5). Тогда исходы, благоприятные для наложения сигналов, представятся заштрихованной областью А. В силу принципа геометрической вероятности искомая вероятность равна отношению площади заштрихованной фигуры к площади всего квадрата:

Пример:

Задача Бюффона. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстояние 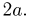Геометрическая вероятность На плоскость наудачу бросается тонкая игла длиной 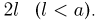Найдем вероятность того, что игла пересечет какую-нибудь прямую (рис. 6). Для этого прежде всего решим, что в данном случае соответствует понятию «наудачу». Ясно, что если игла бросается с достаточной высоты и ее начальное положение случайно, то под словом «наудачу» естественно подразумевать следующее: во-первых, центр иглы наудачу попадет на отрезок длиной 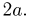Геометрическая вероятность во-вторых, угол 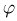между иглой и прямой равномерно распределен на 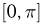и, в-третьих, на величину угла

не влияет расстояние от центра до прямой. Поэтому изобразим результат бросания точкой с координатами 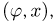Геометрическая вероятность лежащей внутри прямоугольника со сторонами 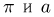(рис. 7), где х — расстояние от центра иглы до ближайшей прямой. Из рис. 6 видно, что пересечение иглы с прямой происходит тогда и только тогда, когда 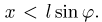Геометрическая вероятность Искомая вероятность равна отношению площади заштрихованной области А к площади прямоугольника:

Задача Бюффона может быть использована для экспериментального определения числа 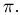Геометрическая вероятность Так, Вольф (Цюрих) бросал иглу 5000 раз и получил 2532 пересечения с прямыми; при этом 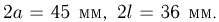Заменяя теперь Р(А) частотой пересечения прямых 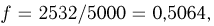получаем эмпирическое значение числа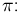 Геометрическая вероятность

Более точное определение числа 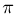Геометрическая вероятность таким путем вряд ли возможно, поскольку, с одной стороны, здесь влияют физические особенности опыта (толщина иглы, неточность при определении факта пересечения и т.д.), с другой стороны, как мы увидим дальше, необходимо производить очень большое число испытаний.

Геометрические вероятности

Вероятное пространство	Условные вероятности
Конечное вероятностное пространство. Классическое определение вероятности	Формула полной вероятности

Решение заданий и задач по предметам:

Дополнительные лекции по теории вероятностей: