Задача 1.28.
Для производства двух видов изделий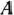 
и 
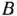предприятие использует три вида сырья. Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в табл. 1.2. В ней же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.
Учитывая, что изделия 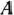и 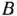могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной.
Решение:
Предположим, что предприятие изготовит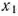 
изделий вида 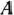и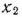 
изделий вида 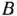. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьем каждого вида и количество изготовляемых изделий не может быть отрицательным, должны выполняться неравенства
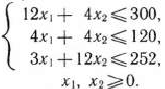
Общая прибыль от реализации 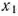изделий вида 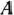и 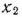изделий вида составит
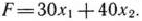
Таким образом, мы приходим к следующей математической задаче: среди всех неотрицательных решений данной системы линейных неравенств требуется найти такое, при котором функция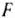 
принимает максимальное значение.
Найдем решение сформулированной задачи, используя ее геометрическую интерпретацию. Сначала определим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств и найдем соответствующие прямые:
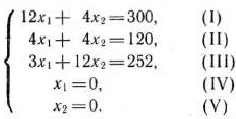
Эти прямые изображены на рис. 1.5. Каждая из построенных прямых делит плоскость на две полуплоскости. Координаты точек одной полуплоскости удовлетворяют исходному неравенству, а другой — нет. Чтобы определить искомую полуплоскость, нужно взять какую-нибудь точку, принадлежащую одной из полуплоскостей, и проверить, удовлетворяют ли ее координаты данному неравенству. Если координаты взятой точки удовлетворяют данному неравенству, то искомой является та полуплоскость, которой принадлежит эта точка, в противном случае — другая полуплоскость.
Найдем, например, полуплоскость, определяемую неравенством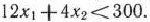 
. Для этого, построив прямую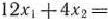 
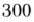(на рис. 1.5 эта прямая 
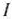), возьмем какую-нибудь точку, принадлежащую одной из двух полученных полуплоскостей, например точку 
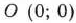. Координаты этой точки удовлетворяют
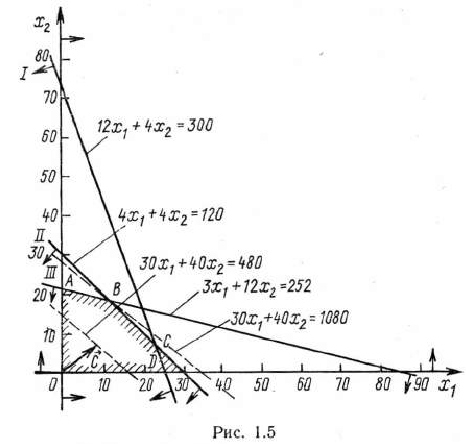
неравенству
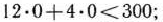
значит, полуплоскость, которой принадлежит точка 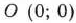, определяется неравенством
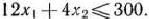
Это и показано стрелками па рис. 1.5.
Пересечение полученных полуплоскостей и определяет многоугольник решений данной задачи.
Как видно из рис. 1.5, многоугольником решений является пятиугольник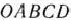 
. Координаты любой точки, принадлежащей этому пятиугольнику, удовлетворяют данной системе неравенств и условию неотрицательности переменных. Поэтому сформулированная задача будет решена, если мы сможем найти точку, принадлежащую пятиугольнику 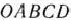, в которой функция 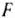принимает максимальное^ значение. Чтобы найти указанную точку, построим вектор 
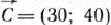и прямую
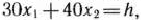
где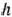 
— некоторая постоянная такая, что прямая 
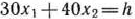имеет общие точки с многоугольником решений. Положим, например, 
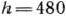и построим прямую 
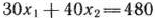(рис. 1.5).
Если теперь взять какую-нибудь точку, принадлежащую построенной прямой и многоугольнику решений, то ее координаты определяют такой план производства издели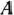й и 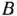, при котором прибыль от их реализации равна 480 руб. Далее, полагая 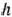равным некоторому числу, большему чем 480, мы будем получать различные параллельные прямые. Если они имеют общие точки с многоугольником решений, то эти точки определяют планы производства издели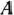й и 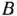, при которых прибыль от их реализации превзойдет 480 руб.
Перемещаядостроенную прямую 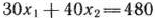в направлении вектора 
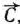, видим, что последней общей точкой ее с многоугольником решений задачи служит точка 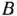. Координаты этой точки и определяют план выпуска издели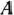й и 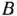, при котором прибыль от их реализации является максимальной.
Найдем координаты точки 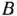как точки пересечения прямых II и III. Следовательно, ее координаты удовлетворяют уравнениям этих прямых
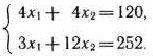
Решив эту систему уравнений, получим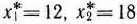 
. Следовательно, если предприятие изготовит 12 изделий вида 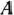и 18 изделий вида 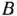, то оно получит максимальную прибыль, равную
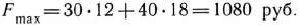
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
