Оглавление:
Дифференциал функции
Если функция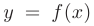 
имеет в точке 
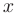отличную от нуля производную 
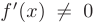, то в соответствии с определением производной. свойствами пределов и бесконечно малых функций приращение этой функции можно записать в виде суммы двух бесконечно малых функций при 
:
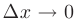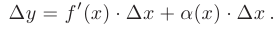
Причем первое слагаемое есть бесконечно малая одного порядка с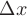 
, а второе слагаемое — бесконечно малая более высокого порядка, так как функция 
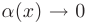при .
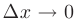Дифференциалом функции 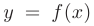в точке 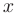называется главная часть ее приращения, линейная относительно 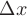, а так как дифференциал независимой переменной равен ее приращению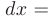 
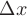, то дифференциал функции можно записать в виде:
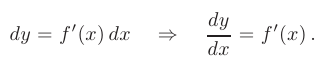
Из последней формулы следует, что производную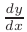 
можно обозначать как отношение дифференциала функции 
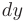к дифференциалу независимой переменной 
.
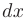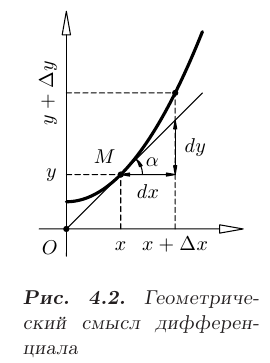
Геометрический смысл дифференциала. Построим график функции 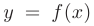и проведем касательную к графику в точке 
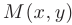. Сравнивая ординаты графика функции и его касательной для абсциссы 
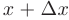; легко увидеть, что главная часть приращения ординаты 
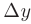линейна относительно приращения абсциссы 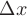и определяется тангенсом угла наклона касательной а к графику функции 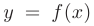, т.е. соответствует дифференциалу этой функции (см. рис. 4.2):
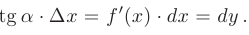
Основные свойства дифференциала. Основные свойства дифференциала функции легко получить, используя связь дифференциала с производной функции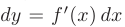 
и основные свойства производной, рассмотренные на стр. 75.
Пример помощи с заданием №4.2.
Требуется найти дифференциал функции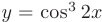 
.
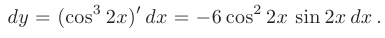
Применение дифференциала в приближенных вычислениях. Из определения дифференциала нам уже известно, что приращение любой дифференцируемой функции можно представить в виде:
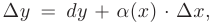
где 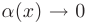при 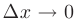. Отбрасывая бесконечно малую более высокого порядка, чем 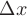получаем приближенное равенство:
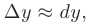
откуда следует, что
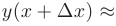
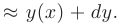
Последнее равенство тем точнее, чем меньше 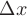. Так как дифференциал функции во многих случаях находится проще, чем ее приращение, то последняя формула получила широкое распространение в вычислительной математике.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
