Деление отрезка в заданном отношении на чертеже

Деление отрезка в заданном отношении на чертеже

На рис. 4.7 показано построение горизонтальной проекци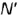и точки 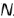, принадлежащей профильной прямой . Построение основано на одном из свойств параллельного проецирования: отношение отрезков прямой линии равно отношению их проекций.

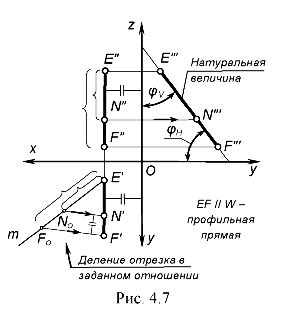
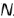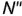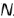Пусть точка делит отрезок в каком-то отношении. Следовательно, проекции отрезка делятся в том же отношении. Если, например, дана фронтальная проекция точки , принадлежащей отрезку , то для построения горизонтальной проекции 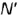на горизонтальной проекции 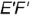отрезка нужно выполнить следующие графические действия:

• провести произвольную прямую 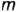из любой вершины горизонтальной проекции ;
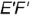• отложить на этой прямой два отрезка: отрезок равный по величине фронтальной проекции , и отрезок , равный по величине ;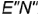
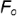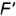• соединить прямой точки и на горизонтальной проекции; из построенной точки 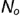провести прямую, параллельную прямой 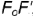— точка 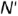и будет искомой.

Прямые проецирующие — перпендикулярные одной плоскости проекций (параллельные двум плоскостям проекций):

фронтально-проецирующие прямые — перпендикулярные плоскости проекций 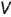(параллельные плоскостям проекци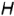й и );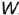

• горизонтально-проецирующие — перпендикулярные плоскости проекций 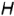(параллельные плоскостям проекци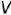й и );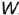
• профильно-проецирующие — перпендикулярные плоскости проекций 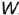(параллельные плоскостям проекци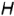й и ).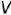

!!! Поскольку положение проецирующих прямых совпадает по направлению с проецирующим лучом к одной из плоскостей проекций, го одна из проекций прямых проецируется (вырождается) в точку. Говорят, что проецирующие прямые обладаю! «собирательным» свойством, так как их вырожденные проекции-точки «собирают», т.е. представляют собой проекции всех точек, лежащих на этих прямых.

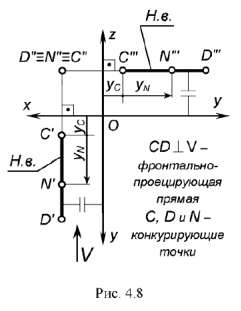
На рис. 4.8 изображены проекции фронтально-проецирующей прямой 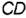и принадлежащей ей точки 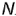. Запомните характерные признаки расположения проекций фронтально-проецирующей прямой на чертеже:

• фронтальная проекция 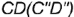представляет собой точку, т.е. фронтальные проекции точек 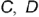и 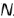совпадают как лежащие на одном проецирующем луче к плоскости проекций ;

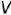• горизонтальная проекция 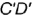расположена перпендикулярно оси проекций 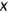и определяет натуральную величину прямой;

профильная проекция 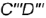но построению располагается перпендикулярно оси проекций 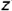и также определяет натуральную величину прямой.

!!! КОНКУРИРУЮЩИЕ ТОЧКИ — точки, лежащие на одном проецирующем луче.

На рис. 4.8 точк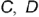и и 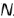на прямой 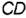являются конкурирующими и по их расположению на прямой относительно плоскости 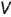(но координатам 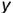) можно определить на горизонтальной проекции порядок их «видимости»: ближе к наблюдателю и дальше от плоскости 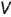(с наибольшей координатой 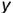) находится точка 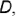. затем точка 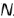и точка .

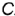На рис. 4.9 изображены проекции горизонтально-проецирующей прямой 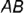и принадлежащей ей точки 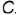. Запомните характерные признаки расположения проекций горизонтально-проецирующей прямой на чертеже:

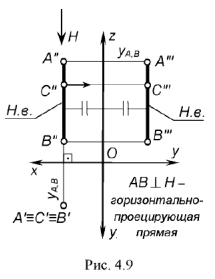
• горизонтальная проекция 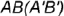представляет собой точку, т.е. горизонтальные проекции точек 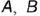и 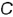совпадают как лежащие на одном проецирующем луче к плоскости проекций :
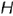• фронтальная проекция 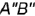расположена перпендикулярно оси 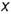и определяет натуральную величину прямой;
• профильная проекция но построению располагается параллельно оси 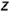и также определяет натуральную величину прямой.

На рис. 4.10 изображены проекции профильно-проецирующей прямой и принадлежащей ей точки 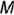. Запомните характерные признаки расположения проекций профильио-проецирую-шей прямой на чертеже:

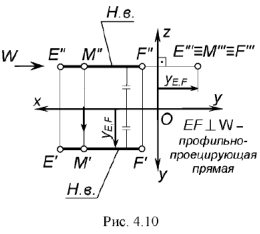
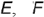профильная проекция представляет собой точку, т.е. профильные проекции точек и 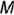совпадают как лежащие на одном проецирующем луче к плоскости проекций ;

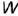фронтальная проекция 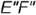расположена параллельно оси 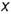и определяет натуральную величину прямой;

горизонтальная проекция по построению также располагается параллельно оси 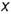и определяет натуральную величину прямой.

Построение на чертеже натуральной величины отрезка прямой общего положения способом прямоугольного треугольника и углов ее наклона к плоскостям проекци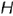й и .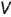

Натуральной величиной заданного на чертеже отрезка прямой общего положения является гипотенуза построенного прямоугольного треугольника, одним катетом которого может быть горизонтальная (или фронтальная) проекция отрезка, а вторым — разница координат 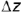(или 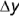) конечных точек этого отрезка относительно оси проекций .

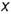На рис. 4.11 показано построение натуральной величины заданного отрезка 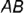способом прямоугольного треугольника относительно фронтальной и горизонтальной его проекций, для чего выполнен следующий графический алгоритм (графические действия):

1-е действие. Провести перпендикулярную линию 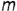к фронтальной проекции 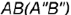отрезка

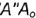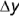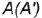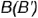2-е действие. Па этой прямой отложить отрезок . равный разнице координат конечных точек и отрезка относительно оси проекций ;

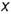3-е действие. Достроить гипотенузу 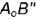треугольника, которая определяет искомую натуральную величину отрезка .

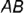Аналогичные построения выполнены проекции отрезка — гипотенуза 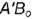величину заданного отрезка.

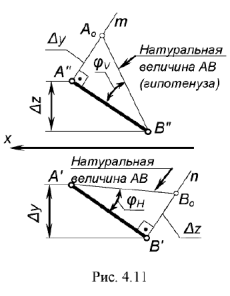
В построенных прямоугольных треугольниках углы между проекциями отрезка и гипотенузой определяют углы наклона прямой к плоскостям проекци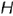й и :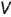

• угол 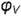между фронтальной проекцией 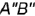отрезка и гипотенузой 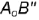определяет наклон отрезка к плоскости проекций ;
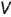• угол 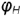между горизонтальной проекцией отрезка и гипотенузой 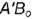определяет наклон отрезка к плоскости проекций .

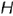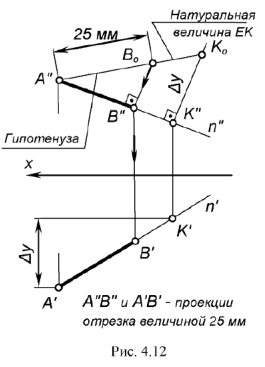
!!! В задачах по начертательной геометрии часто требуется построить на прямой общего положения, не имеющей второй конечной точки, проекции отрезка какой-либо заданной величины.

11а рис. 4.12 показано построение на прямой 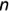с одной конечной точкой 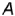проекций отрезка заданной величины 25 мм, для чего выполнен следующий графический алгоритм (графические действия):

1-е действие. Ограничить прямую 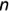произвольным отрезком :

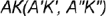2-е действие. Построить натуральную величину произвольного отрезка 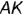способом прямоугольною треугольника относительно, например, фронтальной проекции 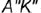— это гипотенуза — 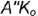(см. рис. 4.11).

3-е действие. На построенной натуральной величине 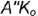(гипотенузе) от точки 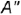отложить отрезок, равный 25 мм, и построить точку .

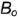4-е действие. Из построенной точки 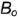провести перпендикуляр на проекцию 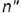заданной прямой 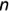и получить точку 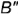, т.е. построить фронтальную проекцию 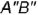отрезка заданной величины 25 мм; по линии связи определить горизонтальную проекцию 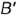точки 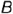, т.е. построить горизонтальную проекцию отрезка заданной величины 25 мм.

Эта теория взята со страницы задач по начертательной геометрии:

• Решение задач по начертательной геометрии

Возможно эти страницы вам будут полезны:

Точка в системе плоскостей проекций h v и w

Прямые общего и частных положений относительно плоскостей проекций

Взаимное положение двух прямых

Теорема о проекции прямого угла