Теорема о проекции прямого угла

Теорема о проекции прямого угла. Частное расположение прямых — перпендикулярные прямые

Пересекающиеся прямые в пространстве могут быть расположены под прямым углом, т.е. взаимно перпендикулярно. Прямой угол между перпендикулярными прямыми может проецироваться на чертеж в натуральную величину при определенном условии.

Теорема о проекции прямого угла :

• если одна сторона прямого угла параллельна какой-либо плоскости проекций, а вторая сторона ей не перпендикулярна, то на эту плоскость проекций угол проецируется в натуральную величину, т.е. прямым (90°).

Па рис. 4.17 дано изображение, поясняющее теорему о проекции прямого угла. Две перпендикулярные прямые 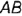и 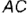, образующие плоскость проецируются на некоторую плоскость проекций 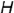. Прямая 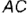по условию параллельна этой плоскости проекций. Доказательство теоремы основано на известной из геометрии теореме о грех перпендикулярах (обратная теорема): прямая 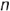, проведенная в плоскости 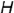перпендикулярно наклонной прямой 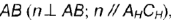, перпендикулярна и ее проекции; следовательно, угол 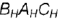— прямой.

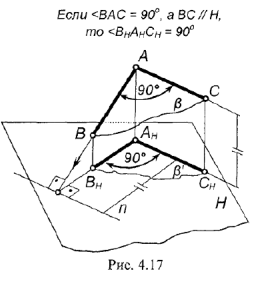
!!! Для решения многих задам начертательной геометрии требуется по условию строить проекции прямого угла.

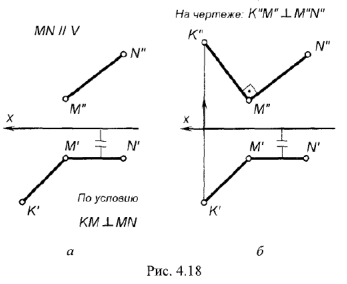
На рис. 4.18. а, б показано построение на чертеже недостающей фронтальной проекции прямого угла .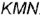

На рис. 4.18, а изображено графическое условие задачи: дана горизонтальная проекция 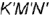прямого угла и фронтальная проекция 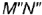одной стороны этого угла.

На рис. 4.18, б показано решение задачи: так как одна сторона 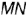прямого угла по условию является фронтальной прямой, т.е. параллельна фронтальной плоскости проекций 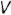, то по теореме о проекции прямого угла на плоскость 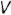заданный прямой угол 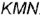должен проецироваться прямым; следовательно, фронтальную проекцию 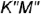стороны 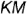прямого угла проводим перпендикулярно заданной фронтальной проекции стороны .

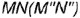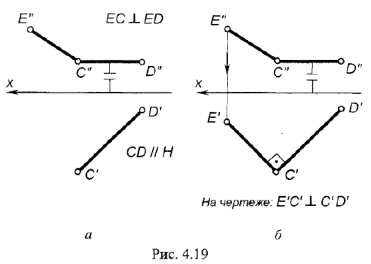
На рис. 4.19, а, 6 показано построение на чертеже недостающей горизонтальной проекции прямого угла .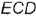

На рис. 4.19, а изображено графическое условие задачи: дана фронтальная проекция прямого угла и горизонтальная проекция 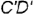одной стороны этого угла.

На рис. 4.19, б показано решение задачи: так как одна сторона 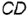прямого угла но условию является горизонтальной прямой. т.е. параллельна горизонтальной плоскости проекций 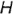, то по теореме о проекции прямого угла на плоскость 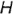заданный прямой угол 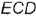должен проецироваться прямым; следовательно, горизонтальную проекцию 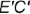стороны угла 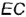проводим перпендикулярно заданной горизонтальной проекции стороны .

Эта теория взята со страницы задач по начертательной геометрии:

• Решение задач по начертательной геометрии

Возможно эти страницы вам будут полезны:

Деление отрезка в заданном отношении на чертеже

Взаимное положение двух прямых

Различные способы задания плоскости на чертеже

Прямые особого положения в плоскости