Контрольная работа К1а.
Даны уравнения движения точки в плоскости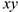 
:
(
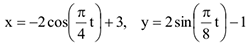
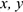— в сантиметрах, 
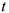— в секундах).
Определить уравнение траектории точки для момента времени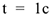 
. Найти скорость и ускорение точки, а также её нормальное и касательное ускорения и радиус кривизны в соответствующей точке траектории.
Решение:
1 Для определения уравнения траектории точки исключим из заданных уравнений движения время 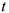. Учитывая конкретный вид функции 
, используем формулу:
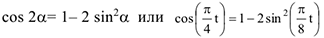
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (а). Получим
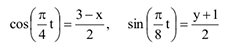
Следовательно,
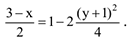
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. К 1а).
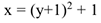
Найдем начало отсчета движения, т.е. точку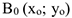 
при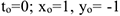 
, следовательно 
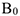(1;-1). Определим также координаты точки при .
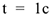Таким образом, точка движется от точки 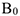к точке 
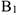и далее. Реализуется верхняя от точки 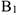ветвь параболы.
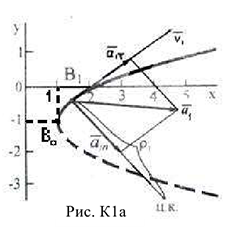
2 Скорость точки найдем по её проекциям на координатные оси
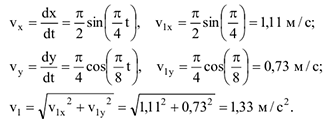
где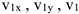 
— значения 
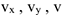при .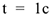
3 Аналогично находим ускорение:
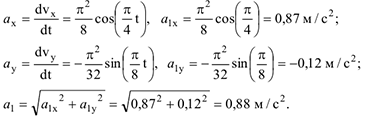
где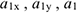 
— значения 
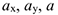при .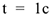
4 Касательное ускорение 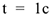находим по формуле:
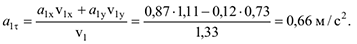
5 Нормальное ускорение 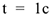определяем с выражения:
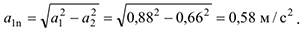
6 При 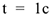радиус кривизны траектории для точки 
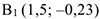равен:
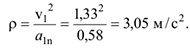
Ответ:
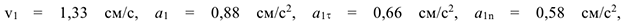
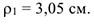
Векторы
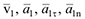
и схематично 
изображаем на рисунке К1а.
Эта контрольная работа взята со страницы готовых контрольных работ по теоретической механике:
Готовые контрольные работы по теоретической механике
Возможно эти контрольные работы будут вам полезны:
