Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной, случайной величины 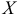, возможные значения которой принадлежат отрезку 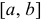, называют:

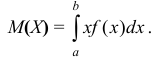
Если возможные значения принадлежат всей оси 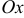, то .

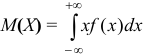Дисперсией непрерывной случайной величины называют математическое ожидание квадрата её отклонения:

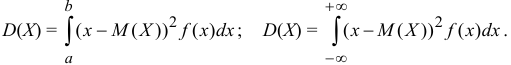
Пример №1

Случайная величина 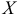распределена на отрезке [2; 4] с плотностью вероятности 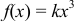Найти коэффициент .

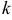Решение:

Все возможные значения случайной величины 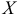принадлежат отрезку [2; 4]. Следовательно, 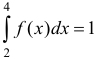. Найдя определенный интеграл, 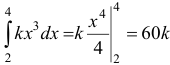, из уравнения 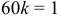получаем .

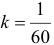Пример №2

Случайная величина задана функцией распределения:

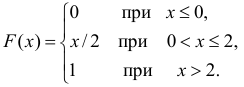
Найти плотность распределения вероятностей, математическое ожидание, дисперсию и вероятность попадания случайной величины в интервал (1/4; 1).

Решение:

Найдем плотность распределения вероятностей 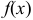. Для этого продифференцируем по 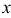интегральную функцию распределения :

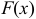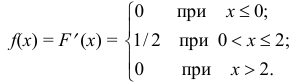
Математическое ожидание 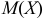для непрерывной случайной величины находится по формуле 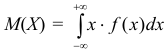, а так как 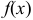вне интервала (0; 2] принимает значение ноль, то .

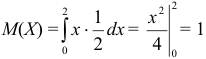Дисперсию удобно вычислить по формуле 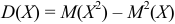, то есть

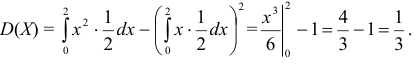
Вероятность попадания значений случайной величины в интервал (1/4; 1] равна определенному интегралу в пределах от 1/4 до 1 от функции плотности распределения вероятностей:

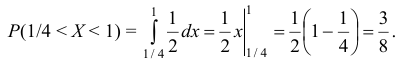
На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:

Теория вероятностей краткий курс для школьников и студентов

Возможно вам будут полезны эти страницы:

Функция распределения случайной величины: свойства и пример с решением

Плотность и свойства распределения вероятностей непрерывной случайной величины

Закон равномерного распределения вероятностей: определение и пример с решением

Закон нормального распределения вероятностей: определение и пример с решением