Если независимой переменной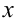 
функции 
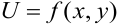дать приращение 
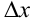не изменяя при этом вторую переменную 
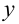, то функция 
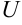получит частное приращение по : 
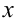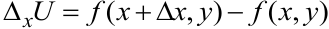. Аналогично определяется частное приращение функции 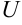по переменной :
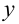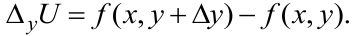
Частной производной по 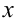функции 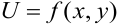называется предел отношения частного приращения функции по переменной 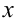, к приращению аргумента 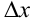при стремлении последнего к нулю.
Частная производная обозначается одним из символов:
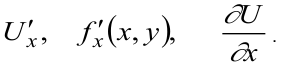
Таким образом,
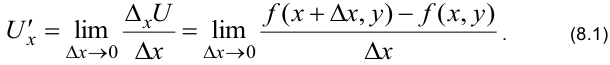
Аналогично, частная производная по
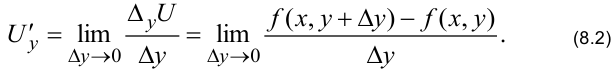
Из определений (8.1) и (8.2) следует, что частная производная по одной переменной вычисляется при условии, что другие независимые переменные являются постоянными величинами. Все правила дифференцирования функции одной переменной сохраняются.
Частные производные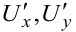 
функции двух переменных в общем случае также являются функциями двух переменных, которые можно дифференцировать по каждой независимой переменной. При этом получим четыре производных второго порядка:
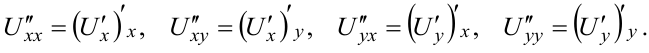
Частные производные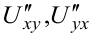 
называют смешанными.
Пример:
Определить частные производные первого и второго порядков от функции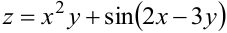 
.
Решение:
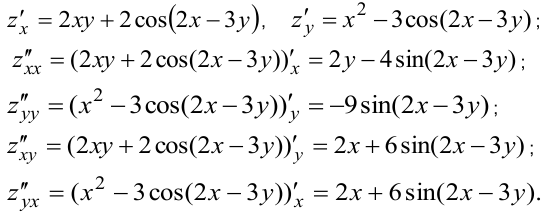
Равенство в примере двух частных смешанных производных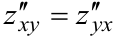 
не является случайным. На этот счёт существует теорема о равенстве частных смешанных производных:
Теорема. Если функция 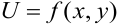и её частные производные первого и второго порядка определены и непрерывны в некоторой области 
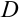, то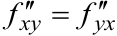 
.
Частные производные обозначаются также символами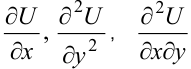 
, что позволяет указать по какой независимой переменной определяется частная производная.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
