Отбор важнейших факторов многофакторных регрессионных моделей
Проблема выбора существенных переменных (факторов) для включения их в модель тесно связана с исходными предпосылками регрессионного анализа. При построении модели два момента вступают в противоречие. В модель должны войти все переменные, которые с экономической точки зрения оказывают влияние на зависимую переменную. Но большое количество переменных, включенных в модель, требует большого числа наблюдений. Невыполнение первого требования может привести к неадекватности модели из-за того, что не учтены некоторые существенные факторы, а также к нарушению нормальности распределения случайной компоненты £ из-за того, что ее вариация будет обусловлена не только случайными факторами, но и систематически действующими, т.е. к нарушению гомоскедастичности. Дж. У. Юл и М. Дж. Кендалл считают, что максимальное число переменных, включенных в модель, не должно превышать десяти.
Сокращение числа переменных, входящих в модель, можно производить путем отсеивания менее существенных факторов в процессе построения регрессионной модели или путем замены исходного набора переменных меньшим числом эквивалентных переменных, полученных в результате преобразований исходного набора.
Процедура отсева несущественных факторов в процессе построения регрессионной модели называется многошаговым регрессионным анализом. Этот метод основан на построении нескольких промежуточных уравнений регрессии, в результате анализа которых получается конечная модель, включающая только факторы, оказывающие существенное влияние на исследуемый показатель. При этом выделяется три подхода.
- Строится уравнение регрессии по максимально возможному количеству факторов, предположительно оказавших влияние на исследуемый показатель. Затем с помощью
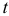 — критерия исключаются несущественные факторы.
— критерия исключаются несущественные факторы. - Строится парная регрессия по одному значимому фактору, а затем в уравнение регрессии последовательно вводятся по одному все значимые факторы. Этот метод называет методом пошаговой регрессии.
- Строится несколько уравнений регрессии, затем с помощью определенного критерия выбирается наилучшее.
Кратко охарактеризуем эти методы построения регрессионных моделей.
Применение 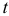 -критерия для отбора существенных факторов основано на предположении о нормальном распределении остатков
-критерия для отбора существенных факторов основано на предположении о нормальном распределении остатков 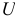 . Если это условие выполняется, то величина
. Если это условие выполняется, то величина 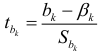 распределена по закону Стьюдента с
распределена по закону Стьюдента с 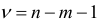 степенями свободы. Задавая уровень значимости
степенями свободы. Задавая уровень значимости 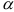 по числу степеней свободы
по числу степеней свободы 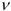 , находят квантиль
, находят квантиль 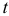 -распределения, с которым сравнивают
-распределения, с которым сравнивают 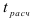 . При
. При 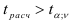 коэффициент регрессии признается статистически значимым с вероятностью
коэффициент регрессии признается статистически значимым с вероятностью 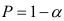 . Если все коэффициенты регрессии признаны значимыми, то уравнение регрессии считается окончательным и при общей проверке его адекватности по
. Если все коэффициенты регрессии признаны значимыми, то уравнение регрессии считается окончательным и при общей проверке его адекватности по 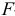 -критерию принимается в качестве модели исследуемого экономического процесса. Если же среди коэффициентов регрессии имеются незначимые, то соответствующие факторы следует исключить из уравнения регрессии, предварительно проранжировав коэффициенты регрессии по значению
-критерию принимается в качестве модели исследуемого экономического процесса. Если же среди коэффициентов регрессии имеются незначимые, то соответствующие факторы следует исключить из уравнения регрессии, предварительно проранжировав коэффициенты регрессии по значению 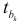 . В первую очередь исключается фактор, для которого значение
. В первую очередь исключается фактор, для которого значение 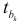 наименьшее. Исключив один фактор с наименьшим значением
наименьшее. Исключив один фактор с наименьшим значением 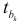 , строят уравнение регрессии без исключенного фактора и снова производят оценку коэффициентов регрессии по
, строят уравнение регрессии без исключенного фактора и снова производят оценку коэффициентов регрессии по 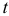 -критерию. Изложенную процедуру повторяют до тех пор, пока все коэффициенты регрессии в уравнении не окажутся значимыми. При этом на каждом шаге, кроме формальной статистической проверки значимости коэффициентов регрессии, проводят экономический анализ несущественных факторов и устанавливают порядок их исключения. В некоторых случаях, исходя из профессиональных соображений, оставляют фактор, для которого
-критерию. Изложенную процедуру повторяют до тех пор, пока все коэффициенты регрессии в уравнении не окажутся значимыми. При этом на каждом шаге, кроме формальной статистической проверки значимости коэффициентов регрессии, проводят экономический анализ несущественных факторов и устанавливают порядок их исключения. В некоторых случаях, исходя из профессиональных соображений, оставляют фактор, для которого 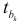 , незначительно меньше
, незначительно меньше 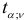 .
.
Отметим, что не существенность коэффициента регрессии по 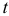 -критерию не всегда является основанием для исключения фактора из дальнейшего анализа. Т. Андерсон рекомендовал исключать переменную из уравнения регрессии лишь в том случае, когда средняя квадратичная ошибка коэффициента регрессии превышает абсолютную величину вычисленного коэффициента, т.е. в случае, если значение
-критерию не всегда является основанием для исключения фактора из дальнейшего анализа. Т. Андерсон рекомендовал исключать переменную из уравнения регрессии лишь в том случае, когда средняя квадратичная ошибка коэффициента регрессии превышает абсолютную величину вычисленного коэффициента, т.е. в случае, если значение 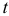 -критерия меньше единицы. При этом предполагается, что нет веских оснований для того, чтобы оставить переменную в модели. При пошаговом построении уравнения регрессии выбирают фактор
-критерия меньше единицы. При этом предполагается, что нет веских оснований для того, чтобы оставить переменную в модели. При пошаговом построении уравнения регрессии выбирают фактор 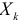 имеющий наибольший коэффициент парной корреляции с
имеющий наибольший коэффициент парной корреляции с 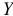 , и строят уравнение парной регрессии. Затем находят частные коэффициенты корреляции между
, и строят уравнение парной регрессии. Затем находят частные коэффициенты корреляции между 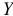 и остальными переменными при исключении выбранной переменной
и остальными переменными при исключении выбранной переменной 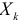 . Переменную с максимальным значением частного коэффициента корреляции включают в уравнение регрессии и вычисляют
. Переменную с максимальным значением частного коэффициента корреляции включают в уравнение регрессии и вычисляют 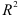 и частный
и частный 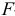 -критерий, который показывает, существенный ли вклад вносит в уравнение эта переменная по сравнению с уже введенными. Указанная процедура проводится до тех пор, пока расчетное значение
-критерий, который показывает, существенный ли вклад вносит в уравнение эта переменная по сравнению с уже введенными. Указанная процедура проводится до тех пор, пока расчетное значение 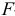 -критерия становится меньше табличного. Подчеркнем, что на каждом шаге с добавлением новой переменной определяется значимость не только новой переменной, но и переменных, уже включенных в модель. И если какие-то из них окажутся незначимыми, они исключаются из уравнения. Значимость определяется значением частного
-критерия становится меньше табличного. Подчеркнем, что на каждом шаге с добавлением новой переменной определяется значимость не только новой переменной, но и переменных, уже включенных в модель. И если какие-то из них окажутся незначимыми, они исключаются из уравнения. Значимость определяется значением частного 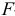 -критерия для всех переменных модели.
-критерия для всех переменных модели.
В многошаговом регрессионном анализе, основанном на методе случайного поиска с адаптацией, разработанным Г.С. Лбовым, применяют «поощрение» или «наказание» отдельных переменных исходя из их «ценности». В качестве критерию «ценности» используют коэффициент множественной корреляции 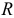 .
.
В начале поиска задают равные вероятности 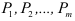 для каждого из факторов. Затем случайным образом выбирают
для каждого из факторов. Затем случайным образом выбирают 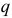 групп по
групп по 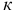 факторов и в этой системе определяют
факторов и в этой системе определяют 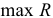 и
и 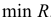 . Векторы факторов в первой системе
. Векторы факторов в первой системе 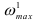 и
и 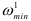 запоминают. Вероятность попадания в систему
запоминают. Вероятность попадания в систему 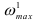 увеличивается, а в
увеличивается, а в 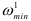 уменьшается на
уменьшается на 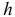 (
(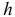 — произвольное число). Так образовывают
— произвольное число). Так образовывают 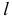 систем по
систем по 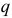 групп в каждой. За эффективную принимают ту группу, при которой
групп в каждой. За эффективную принимают ту группу, при которой
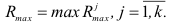
При переборе ряда групп вероятность выбора факторов, часто встречающихся в удачных сочетаниях, становится большей, и именно этот набор факторов повторяется гораздо чаще остальных. Число 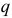 выбирают так, чтобы между значениями
выбирают так, чтобы между значениями 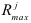 и
и 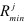 данной системы
данной системы 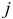 была заключена основная часть сочетаний, а величину шага
была заключена основная часть сочетаний, а величину шага 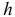 — такой, чтобы вероятность выбора фактора, если он будет встречаться на каждом этапе, оставалась большей или равной установленной вероятности
— такой, чтобы вероятность выбора фактора, если он будет встречаться на каждом этапе, оставалась большей или равной установленной вероятности 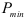 . При увеличении шага растет и доля случаев, когда эффективное сочетание факторов не будет найдено. При
. При увеличении шага растет и доля случаев, когда эффективное сочетание факторов не будет найдено. При 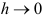 эффективный поиск сводится к методу Монте-Карло. В этом методе отсутствует статистическая проверка значимости коэффициентов регрессии.
эффективный поиск сводится к методу Монте-Карло. В этом методе отсутствует статистическая проверка значимости коэффициентов регрессии.
Из предложенных подходов построения регрессионной модели выделяют первый, основанный на оценке значимости коэффициентов регрессии по критерию Стьюдента.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

