Построение многофакторной линейной регрессионной модели
Связи между массовыми экономическими явлениями характеризуются тем, что в действительности некоторое явление детерминируется множеством одновременно и совокупно действующих причин. Поэтому в общем случае зависимая переменная может быть функцией нескольких переменных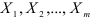 
и вместо парной регрессии рассматривается множественная регрессия:
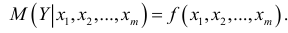
В каждом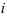 
-м наблюдении получаем совокупность значений независимых переменных 
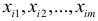и соответствующее значение зависимой переменной 
.
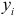Предположим, что между независимыми переменными 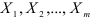и зависимой переменной 
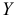существует линейное соотношение. Тогда уравнение
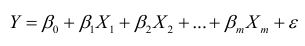
выражающее линейное соотношение между переменными, называется теоретическим уравнением множественной регрессии, а соответствующее эмпирическое уравнение регрессии будет иметь вид:
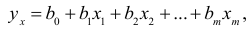
Ясно, что указанным уравнением невозможно охватить весь комплекс причин и учесть случайность, присущую в той или иной степени причинному действию и определенному им следствию. Ограничиваясь наиболее важными факторами, влияющими на развитие исследуемого явления, в выражение функции регрессии вводят аддитивную составляющую — возмущающую переменную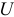 
, дающую суммарный эффект от воздействия всех неучтенных факторов и случайностей. Возмущение и является случайной переменной, математическое ожидание 
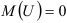, дисперсия возмущений 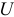постоянна. Поэтому эмпирическое значение величины 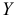можно представить следующим образом:
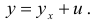
В выражении (2.1)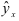 
— это среднее значение переменной 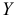в точке 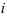при фиксированных значениях 
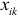независимых переменных
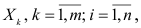
в предположении, что только эти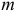 
переменных являются причиной изменения переменной 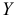. Значения 
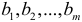— это оценки коэффициентов регрессии 
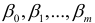. Так, например, 
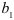указывает среднюю величину изменения 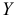при изменении 
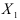на одну единицу при условии, что другие переменные остаются без изменения; 
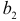указывает среднюю величину изменения 
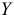при изменении 
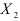на одну единицу при условии, что другие переменные остались без изменения, и т.д. Свободный член регрессии 
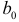определяет точку пересечения гиперповерхности регрессии с осью ординат. Итак, регрессия (2.1) охватывает совокупное одновременное влияние независимых переменных, а коэффициенты регрессии 
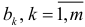, указывают соответствующие усредненные частные влияния переменных 
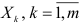в предположении, что остальные независимые переменные сохраняются на постоянном уровне.
Обозначив через
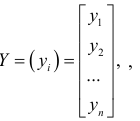
матрицу-столбец зависимой переменной , через
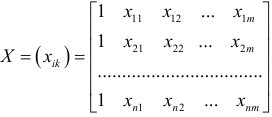
матрицу независимых переменных, размер которой определяется числом наблюдений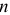 
и числом переменных 
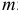; через
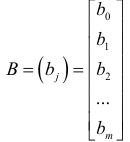
матрицу-столбец коэффициентов регрессии; через
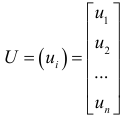
матрицу-столбец возмущений, перепишем линейную модель (2.2) в виде
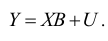
Для вычисления коэффициентов уравнения регрессии составим сумму квадратов отклонений:
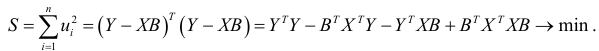
Так как
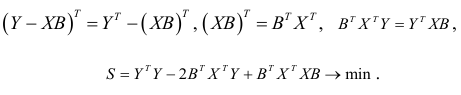
Необходимым условием экстремума служит обращение в нуль частных производных функции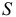 
по параметрам. Дифференцируем 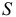по 
, по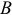лучаем
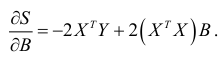
Приравнивая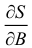 
нулю, находим систему нормальных уравнений, которая в матричной форме имеет вид
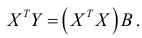
Решение полученной системы определяется по формуле
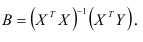
Оценку параметров уравнения регрессии, найденную по формуле (2.3) называют оценкой метода наименьших квадратов.
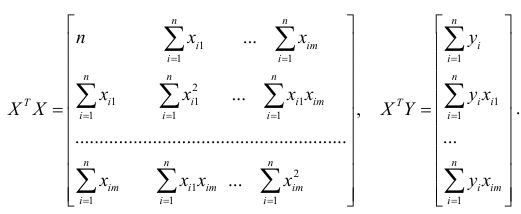
В уравнении (2.3) матрицы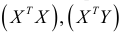 
записываются в следующем виде:
Рассмотрим процедуру построения множественной регрессии с двумя независимыми переменными, не прибегая к обращению матрицы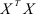 
. Функция линейной множественной регрессии в этом случае имеет вид
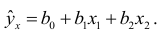
Сумма квадратов отклонений всех наблюдаемых значений зависимой переменной от значений, вычисленных по уравнению регрессии, должна быть минимальна:
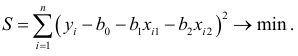
Продифференцировав 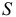по каждому из параметров 
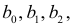приравняв частные производные нулю и выполнив элементарные преобразования, получаем следующую систему нормальных уравнений:
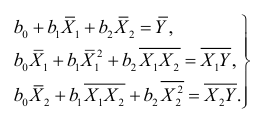
Из первого уравнения системы найдем
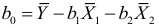
и, подставив в (2.4), получим уравнение регрессии
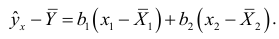
Продолжив решение системы (2.5), найдем параметры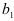 
и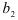 
уравнения регрессии (2.4) по формулам:
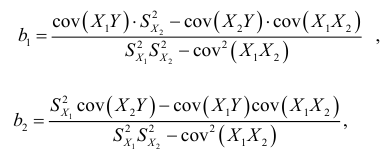
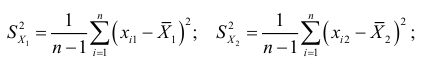
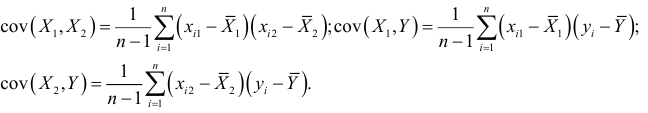
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
| Оценка адекватности регрессионной модели |
| Пример построения однофакторной регрессионной модели |
| Многофакторная линейная регрессионная модель в нормированной размерности |
| Линейная частная регрессия |
