Функциональным называется ряд, членами которого являются функции действительной переменной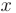 
и натуральной переменной 
:
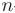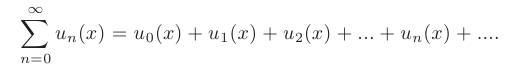
При любом фиксированном значении 
функциональный ряд вырождается в числовой ряд, который либо сходится (абсолютно или условно), либо расходится.
Степенным рядом называется функциональный ряд вида:
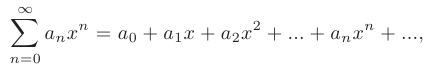
где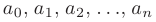 
— постоянные вещественные числа, называемые коэффициентами степенного ряда.
Областью сходимости степенного ряда называется множество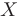 
всех значений 
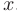, для которых он сходится. Доказано, что областью сходимости степенного ряда является интервал 
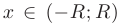. В каждой точке этого интервала ряд сходится, а вне этого интервала, т.е. при 
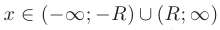— расходится. Интервал 
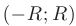называется интервалом сходимости степенного ряда, a 
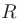— его радиусом сходимости. Для некоторых рядов интервал сходимости вырождается в точку: 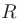= 0, а для других может совпадать с осью 
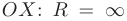. В точках 
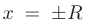ряд может как сходиться, так и расходиться. В каждом конкретном случае этот вопрос решается индивидуально, с помощью исследования соответствующих числовых рядов. Если степенной ряд является полным (т.е. содержит все степени переменной 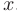), то наиболее часто употребляемые формулы для вычисления радиуса сходимости степенного ряда имеют вид:
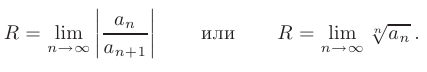
Свойства степенных рядов
- Сумма степенного ряда
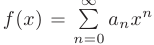есть непрерывная на отрезке 
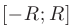функция. - Если степенной ряд 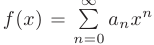сходится на интервале 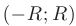, то степенные ряды, полученные почленным дифференцированием и почленным интегрированием этого ряда имеют тот же интервал сходимости .
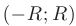Пример:
Найти область сходимости степенного ряда
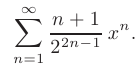
► Если обозначить радиус сходимости степенного ряда как 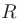, то областью его сходимости является интервал 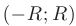и, возможно, границы этого интервала.
Заданный степенной ряд содержит все натуральные степени переменной 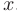, следовательно, радиус его сходимости может быть найден по формуле:
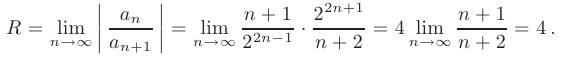
Вопрос о принадлежности границ интервала к области сходимости решается с помощью исследования поведения числового ряда 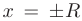при 
. При 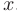= —4 получим знакочередующийся числовой ряд:
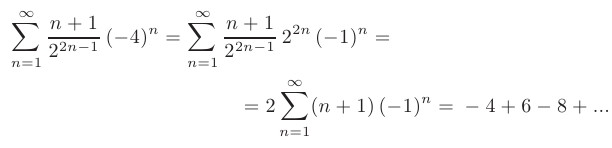
Предел абсолютного значения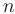 
-го члена полученного ряда не равен нулю:
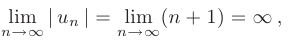
следовательно, согласно признаку Лейбница данный числовой ряд является расходящимся. При 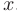= 4 получим знакопостоянный числовой ряд, который в силу необходимого признака сходимости также является расходящимся:
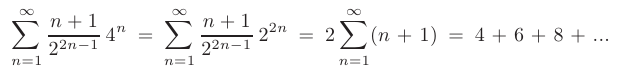
Объединяя полученные результаты, можно записать область сходимости заданного степенного ряда в виде открытого интервала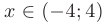 
.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
