Оглавление:
Производные основных элементарных функций
Нахождение производных (дифференцирование) непосредственно по определению даже для простых элементарных функций часто связано с определенными трудностями. Поэтому на практике подобные функции дифференцируют с помощью системы специально выведенных правил и формул. Перечень формул для производных основных элементарных функций приведен в приложении В. 10. Производные остальных элементарных функций можно получить, используя эти формулы и основные свойства производной.
Основные свойства производной. Пусть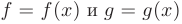 
две дифференцируемые на некотором интервале 
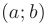функции.
- Производная суммы (разности) двух функций
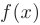и 
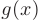равна сумме (разности) производных этих функций:
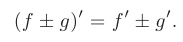
- Производная произведения двух функци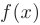й и 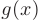равна сумме произведений производной первой функции на вторую и первой функции на производную второй:
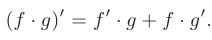
- Постоянную
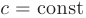можно выносить за знак производной:
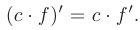
- Производная частного двух функци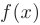й и 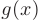, если делитель не равен нулю, равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а ее знаменатель есть квадрат прежнего знаменателя:
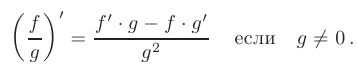
- Производная композиции или сложной функции
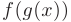равна произведению производной данной функции 
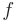по промежуточной переменной 
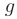на производную промежуточной переменной 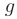по независимой переменной 
:
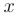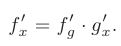
- Производная функции
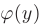, обратной к данной 
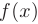, равна величине, обратной к производной данной функции:
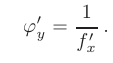
Заметим, что свойства 1, 2 и 5 остаются справедливыми для любого конечного числа слагаемых, сомножителей или промежуточных переменных.
Пример:
Требуется найти производные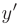 
от заданных функций, пользуясь основными правилами и формулами дифференцирования:
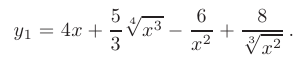
► Прежде чем дифференцировать функцию, целесообразно упростить ее выражение:
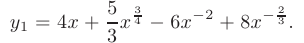
Тогда: 3
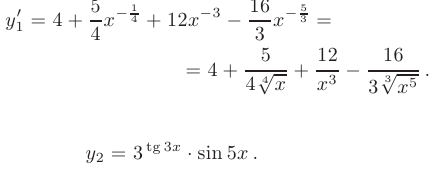
► Данная функция представляет произведение двух функций, каждая из которых является сложной функцией. Поэтому
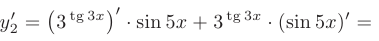
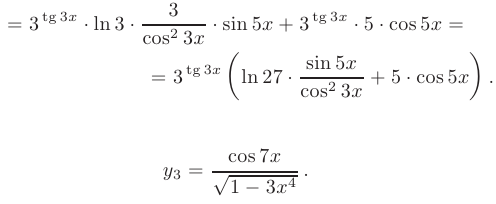
► По правилу дифференцирования частного двух сложных функций:
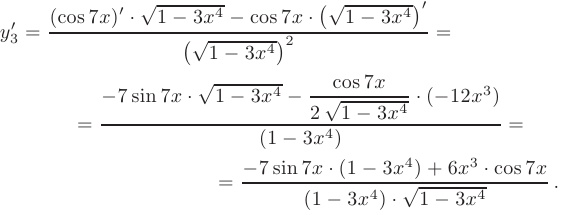
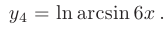
По правилу дифференцирования сложной функции:
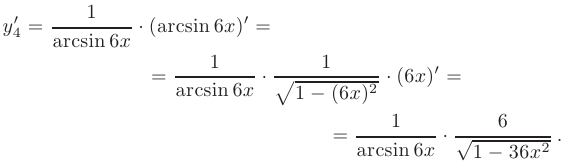
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Асимптоты графика функции в математике |
| Определение производной функции в математике |
| Дифференциал функции в математике |
| Производные и дифференциалы высших порядков в математике |
