Оглавление:
Непрерывность функции
Первое определение непрерывности
Функция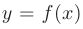 
, определенная в окрестности точки 
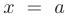, называется непрерывной в точке 
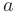, если существует предел функции при 
и он равен значению функции в этой точке:
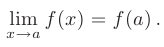
Из определения предела следует, что бесконечно малому приращению аргумента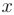 
соответствует бесконечно малое приращение функции 
:
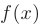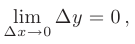
где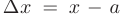 
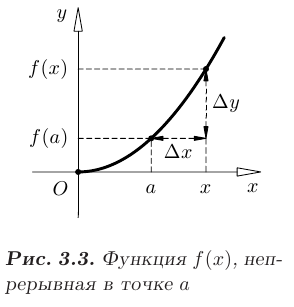
— приращение аргумента;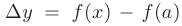 
— приращение функции. Пример графика функции 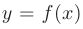, непрерывной в точке 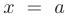показан на рис. 3.3.
Второе определение непрерывности
Функция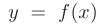 
, определенная в окрестности точки 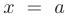, называется непрерывной в точке 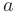, если существуют односторонние пределы функции при 
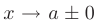и они равны значению функции в этой точке:
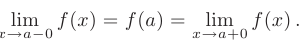
Свойства функций, непрерывных в точке
- Если функци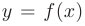и
и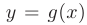 
непрерывны в точке 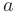, то непрерывными в этой точке являются и функции: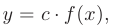 
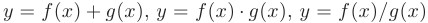при условии, что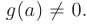 
- Если функция 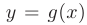непрерывна в точке 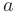, а функция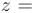
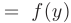непрерывна в точке 
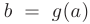, то сложная функция 
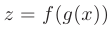также непрерывна в точке .
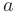Функция 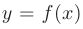называется непрерывной на интервале 
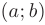, если она непрерывна в каждой точке этого интервала. Функция 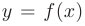называется непрерывной на отрезке 
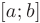если она непрерывна в каждой внутренней точке соответствующего интервала, а на концах отрезка непрерывность определяется односторонними пределами:
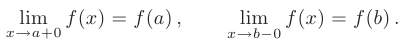
Все основные элементарные функции непрерывны при всех значениях аргумента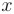 
, для которых они определены. Более того, всякая элементарная функция непрерывна в каждой точке, в которой она определена. Заметим, что основными элементарными функциями считаются: степенные 
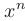, показательные 
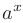, логарифмические 
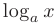, тригонометрические 
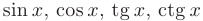и обратные тригонометрические 
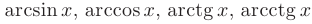функции. Свойства основных элементарных функций описаны в приложении В.8. При этом элементарной называется всякая функция, которую можно задать одной формулой с применением конечного числа арифметических действий и суперпозиций (операций образования сложной функции) над основными элементарными функциями.
Величины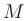 
и 
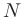называются наибольшим и наименьшим значениями функции 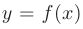на отрезке 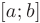, если на этом отрезке существуют такие значения аргумента функци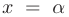и 
и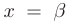 
, что для всех 
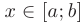верно:
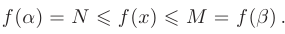
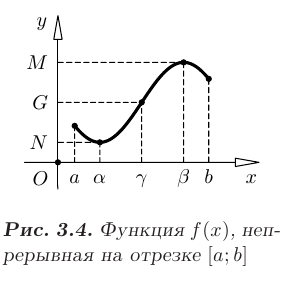
Пример графика функции 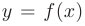, непрерывной на отрезке 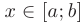показан на рис. 3.4.
Теорема Вейерштрасса. Если функция 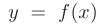непрерывна на отрезке 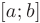, то она ограничена на этом отрезке и достигает на этом отрезке своего наибольшего (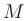) и наименьшего (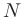) значений.
Теорема Больцано-Коши. Если функция 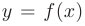непрерывна на отрезке 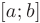, то для всякого значения 
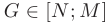найдется точка 
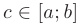такая, что 
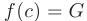(см. рис. 3.4).
Следствие. Если функция 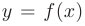непрерывна на отрезке 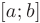и на его концах принимает значения разных знаков, то найдется хотя бы одна точка 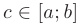такая, что 
.
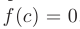Точки разрыва. Точки 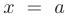, в которых нарушается хотя бы одно условие непрерывности функции 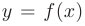, называются точками разрыва этой функции.
Все точки разрыва функции 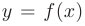разделяются на точки устранимого разрыва первого рода, точки конечного или неустранимого разрыва первого рода и точки бесконечного разрыва или разрыва второго рода.
- Функция 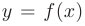определена в точке 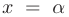и ее окрестности, существует предел
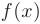при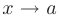 
, но этот предел не равен значению функции в предельной точке 
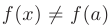при 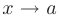. В этом случае точку 
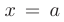называют точкой устранимого разрыва первого рода. Например, функция
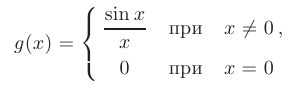
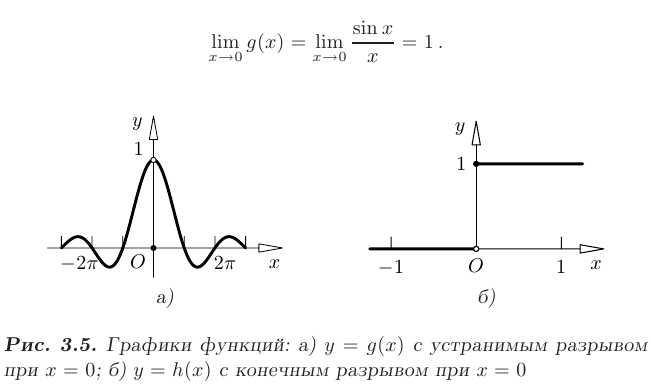
имеет в точке 
устранимый разрыв первого рода (см. рис. 3.5, а), так как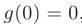 
, в то же время:
- Функция 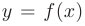определена в точке 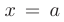и ее окрестности, но не существует предела 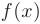при 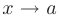. так как односторонние пределы в этой точке существуют, но не равны друг другу. В этом случае точку 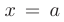называют точкой конечного или неустранимого разрыва первого рода. Например, функция
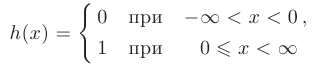
имеет в точке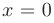 
конечный разрыв первого рода (см. рис. 3.5,6). Действительно, функция определена в точке 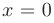, однако ее односторонние пределы в этой точке не равны друг другу:
- Функция
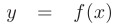определена в окрестности точки 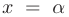, но не определена в самой точке 
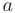. Это происходит когда хотя бы один из односторонних пределов функции 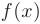в точке а не существует или равен бесконечности. В этом случае точку 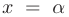называют точкой бесконечного разрыва или разрыва второго рода. Например, функция
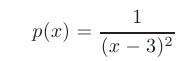
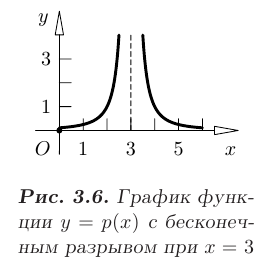
имеет бесконечный разрыв в точке 
(см. рис. 3.6), так как оба односторонних предела при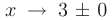 
равны бесконечности:
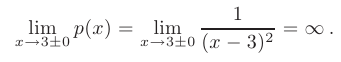
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Бесконечно малые и бесконечно большие функции в математике |
| Раскрытие неопределённостей в математике |
| Асимптоты графика функции в математике |
| Определение производной функции в математике |
