Ранг матрицы
Рангом матрицы называется наивысший порядок отличных от нуля миноров. Минор с наивысшим порядком называется базисным. Ранг матрицы 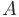 обозначается
обозначается 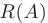 или
или 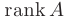 .
.
Элементарными преобразованиями прямоугольной матрицы 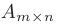 называются такие операции над ее элементами, которые не меняют ранга матрицы. К элементарным преобразованиям матрицы относятся следующие операции:
называются такие операции над ее элементами, которые не меняют ранга матрицы. К элементарным преобразованиям матрицы относятся следующие операции:
- Умножение любой строки матрицы на произвольной число, отличное от нуля;
- Перестановка двух любых строк матрицы;
- Сложение одной из строк матрицы с любой другой строкой той же матрицы, умноженной на произвольный коэффициент (линейное комбинирование строк).
Матрицу 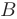 , полученную из
, полученную из 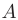 путем элементарных преобразований, называют эквивалентной матрице
путем элементарных преобразований, называют эквивалентной матрице 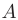 и записывают это утверждение в виде
и записывают это утверждение в виде 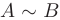 .
.
Заметим, что с помощью элементарных преобразований прямоугольную матрицу 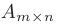 , где
, где  , всегда можно привести к трапециевидной форме, содержащей ровно
, всегда можно привести к трапециевидной форме, содержащей ровно 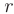 ненулевых строк, причем число таких строк
ненулевых строк, причем число таких строк 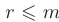 будет точно соответствовать рангу матрицы
будет точно соответствовать рангу матрицы 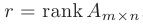 .
.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Обратная матрица в математике |
| Системы линейных уравнений n*n в математике |
| Системы линейных уравнений m*n в математике |
| Собственные значения и собственные векторы матрицы в математике |

