Определитель матрицы
Определителем или детерминантом квадратной матрицы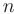 
-го порядка называют число, представляющее собой алгебраическую сумму произведений полного числа сочетаний элементов, принадлежащих различным строкам и столбцам матрицы.
Приняты следующие обозначения определителя матрицы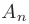 
:
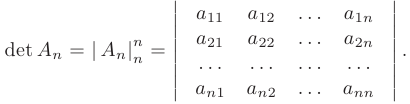
Определителем матрицы 1-го порядка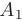 
называется число, равное ее единственному элементу: 
.
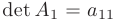Определителем матрицы 2-го порядка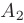 
называется число, равное разности произведений элементов ее главной и вспомогательной диагоналей: 
.
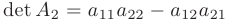Определители матриц более высоких порядков удобнее всего вычисляются с помощью разложения по элементам произвольной строки или столбца. Для вычисления определителей таких матриц рассмотрим новые понятия.
Минором элемента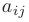 
квадратной матрицы 
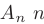-го порядка называется определитель матрицы ( 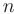— 1) порядка, полученной из матрицы 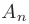после вычеркивания 
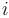-ой строки и 
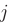-гo столбца, на пересечении которых находится элемент в^. Например, миноры для элементов 2-ой строки матрицы 3-го порядка будут иметь вид
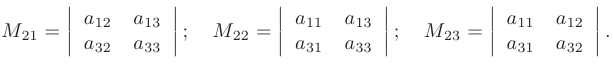
Алгебраическим дополнением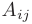 
элемента 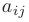матрицы 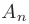называется его минор, взятый со знаком 
:
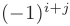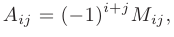
т.е., если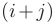 
— четное число, то 
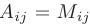, если 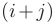— нечетное число, то 
.
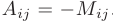Согласно теореме Лапласа определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Разложение по элементам 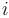-ой строки 
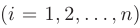определителя матрицы 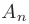имеет вид
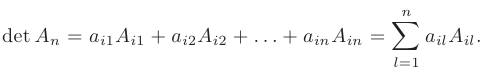
Разложение по элементам 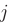-го столбца 
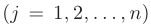определителя матрицы 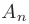имеет вид
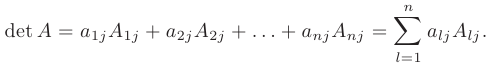
Например, разложение определителя матрицы 3-го порядка по элементам 2-ой строки имеет вид
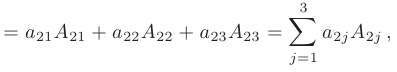
где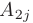 
— алгебраическое дополнение элемента 
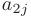матрицы 
.
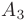Свойства определителей
- При транспонировании квадратной матрицы ее определитель не изменяется:
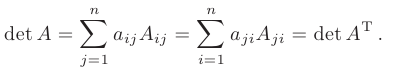
Из этого свойства следует, что все утверждения, сделанные для строк определителя, справедливы и для его столбцов.
- Если матрица содержит нулевую строку или столбец, то ее определитель равен нулю:
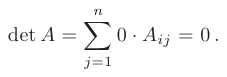
- Постоянный множитель для всех элементов какой-либо строки или столбца матрицы можно выносить за знак определителя:
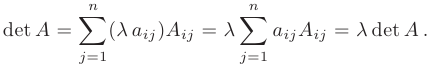
- Определитель, каждый элемент произвольной строки которого является суммой двух слагаемых, равен сумме двух определителей у одного из которых в указанной строке стоят первые слагаемые, а у другого — вторые, при условии, что остальные элементы у всех определителей совпадают, например:
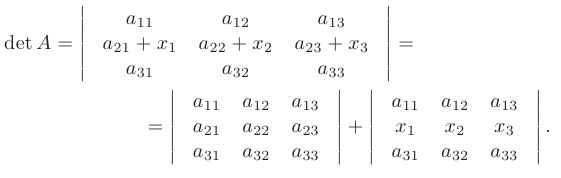
- Если матрица
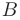получена из матрицы 
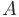путем перестановки двух произвольных строк или столбцов, то ее определитель изменит знак: 
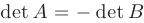. - Если матрица 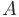имеет две одинаковые или пропорциональные строки или столбцы, то ее определитель равен нулю:
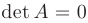. - Определитель матрицы не изменится, если к произвольной её строке прибавить другую строку, умноженную на любое число.
- Определитель произведения двух квадратных матриц одинакового порядка 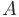и 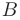равен произведению их определителей:
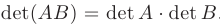. - Определитель треугольной матрицы равен произведению её диагональных элементов.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Матрица в математике |
| Операции над матрицами в математике |
| Обратная матрица в математике |
| Системы линейных уравнений n*n в математике |
