Векторная функция действительного аргумента
Зависимость, по которой каждому действительному числу t из некоторого интервала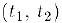 
ставится в соответствие определенный вектор 
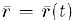на плоскости или в пространстве, называется векторной функцией действительного аргумента.
Для определенности всюду в этом параграфе векторную функцию мы будем рассматривать в пространстве. Пусть в нем выбрана декартова система координат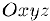 
. Поскольку вектор 
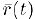в пространстве однозначно определяется своими координатами 
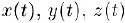в ортонормированием базисе 
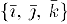и наоборот, то -задание векторной функции
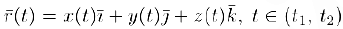
равносильно заданию трех ее функций-координат
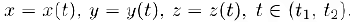
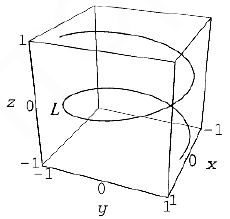
Если зафиксировать начало вектора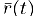 
в начале координат, то его конечная точка при изменении параметра t будет перемещаться по кривой L. имеющей параметрические уравнения (2). Эту кривую мы будем называть траекторией векторной функции 
.
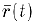Замечание 1. В физике и механике уравнение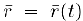 
представляет собой векторное уравнение движения материальной точки, а траектория движения этой точки представляет собой линию в пространстве с параметрическими уравнениями (2).
Введем теперь определение предельного вектора для векторной функции r(t), определенной в интервале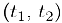 
, содержащем точку 
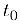за исключением, возможно, этой точки.
Определение 1. Вектор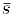 
называется предельным для векторной функции 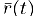при t стремящемся к 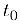, если для любого положительного числа с найдется положительное число 
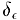, такое., что
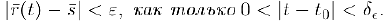
Обозначается этот, предельный вектор через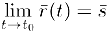 
.
Пусть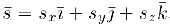 
Теорема. Предельный вектор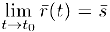 
существует тогда и только тогда, когда существуют пределы, координат (2) векторной функции (1) и
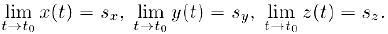
Для доказательства заметим прежде всего, что для любых действительных чисел
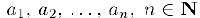
справедливо двойное неравенство
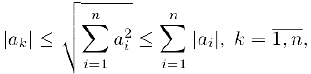
которое мы можем доказать возведением в квадрат всех трех его частей. Теперь, чтобы убедиться в справедливости приведенного выше утверждения, достаточно воспользоваться определением предельного вектора векторной функции и неравенством (3), благодаря которому
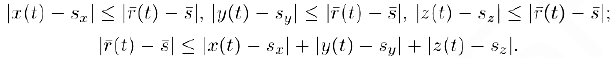
Действительно, из первых трех неравенств (4) следует, что как только
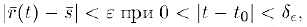
то и
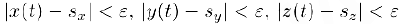
для тех же значений t. Таким образом,
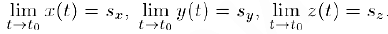
Наоборот, если имеют место последние равенства, то. выбрав по заданному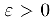 
положительное число 
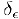так, чтобы
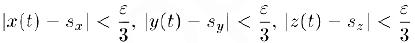
для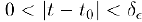 
, мы, воспользовавшись последним из неравенств (4). получим, что
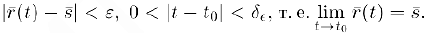
Tеoрeма доказанa.
Из доказанной теоремы и свойств предела функции (глава IV’, §4, пункт 2) следует, что. если существуют предельные векторы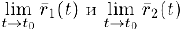 
, то
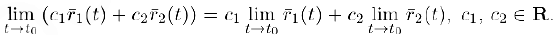
Использовав, кроме того, формулы для вычисления скалярного и векторного произведений (глава 11. §§3, 4). получим:
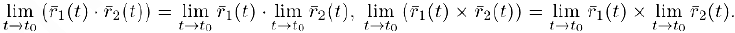
Если, вдобавок, существует еще и предельный вектор 
. то по формуле для представления смешанного произведения в координатах (глава II. §5) будем иметь:
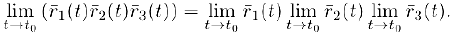
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
