Бесконечно малые (бесконечно большие) функции, их свойства и использование
Функция 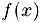 , определенная в некотором интервале, содержащем точку
, определенная в некотором интервале, содержащем точку 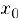 , кроме, возможно. самой этой точки, называется бесконечно малой (бесконечно большой) в точке
, кроме, возможно. самой этой точки, называется бесконечно малой (бесконечно большой) в точке 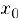 , если существует и равен нулю (бесконечности) предел
, если существует и равен нулю (бесконечности) предел 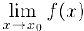 .
.
Изучим сначала свойства бесконечно малых. Очевидно, прежде всего, что вместе с бесконечно малыми 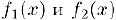 в точке
в точке 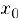 таковыми являются и функции
таковыми являются и функции
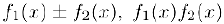
Произведение 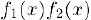 будет бесконечно малой и в случае, когда одна из этих функций является бесконечно малой, а вторая ограничена. Действительно, пусть
будет бесконечно малой и в случае, когда одна из этих функций является бесконечно малой, а вторая ограничена. Действительно, пусть 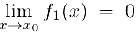 . а
. а 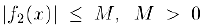 в области определения. Зафиксируем произвольное число
в области определения. Зафиксируем произвольное число 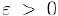 . По определению предела для положительного числа
. По определению предела для положительного числа 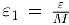 найдется положительное число
найдется положительное число 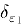 такое, что
такое, что 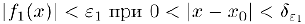 . Тогда при всех таких х
. Тогда при всех таких х
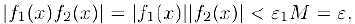
т.e. 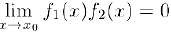 .
.
Частное 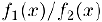 мы будем использовать для сравнения бесконечно малых
мы будем использовать для сравнения бесконечно малых 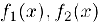 в точке
в точке 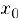 .
.
Будем говорить, что бесконечно малая  имеет, порядок малости k относительно бесконечно малой
имеет, порядок малости k относительно бесконечно малой 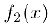 если существует
если существует
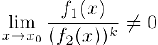
В частности, если 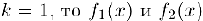 являются бесконечно малыми одного порядка. Если, сверх того.
являются бесконечно малыми одного порядка. Если, сверх того.
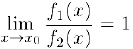
то бесконечно малые 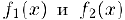 называются эквивалентными. Для эквивалентных бесконечно малых используется обозначение:
называются эквивалентными. Для эквивалентных бесконечно малых используется обозначение: 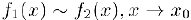 .
.
Наконец, если окажется, что
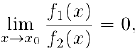
то условимся говорить, что бесконечно малая  имеет более высокий порядок малости относительно бесконечно малой
имеет более высокий порядок малости относительно бесконечно малой 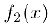 и обозначать этот факт через
и обозначать этот факт через 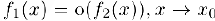 .
.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
| Предел функции: определение и его свойства |
| Два важных правила в анализе предела |
| Определение непрерывности функции. Общие свойства непрерывности |
| Классификация точек разрыва функции с примером |

