Пусть числовая функция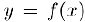 
определена в некотором интервале 
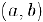. содержащем точку .То, кроме, возможно, самой точки 
.
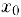Определение. Действительное число L называется пределом функции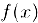 
при 
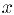стремящемся к 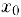. если для любого (можно считать, сколь угодно малого) положительного числа 
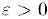существует положительное. число 
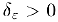такое, что при всех
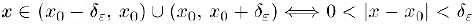
выполняется неравенство
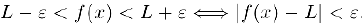
Обозначения для предела: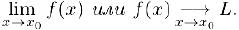 
.
Проиллюстрируем понятие предела функции на ее графике.
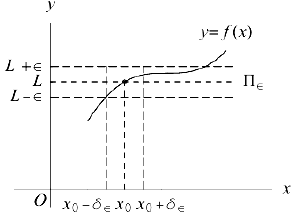
Число L является пределом функци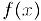и 
при 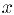стремящемся к 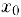, если для всякой сколь угодно узкой полосы 
между горизонтальными прямыми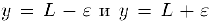 
найдется достаточно малый интервал, симметричный относительно точки 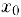, такой, что для всех чисел 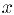из этого интервала соответствующие точки графика функции попадают в полосу .
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
