Оглавление:
Полный дифференциал фнп и его использование в приближенных вычислениях
Определение 15.1. Полным дифференциалом 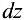 дифференцируемой в точке
дифференцируемой в точке 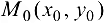 функции
функции 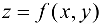 называется главная, линейная относительно приращений
называется главная, линейная относительно приращений 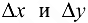 , часть полного приращения этой функции в точке
, часть полного приращения этой функции в точке 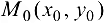 , т. е.
, т. е.
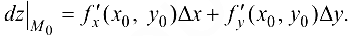
Напомним (см. раздел 2), что для независимых переменных 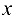 и
и 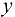 их любые приращения
их любые приращения 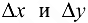 считают дифференциалами:
считают дифференциалами: 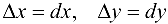 .
.
Тогда полный дифференциал функции 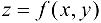 можно записать в виде
можно записать в виде
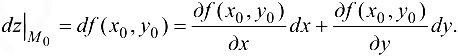
Полный дифференциал имеет широкое применение в приближенных вычислениях. Если рассмотреть функцию 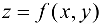 , дифференцируемую в точке
, дифференцируемую в точке 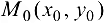 , то
, то
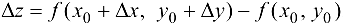
откуда
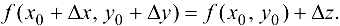
Так как 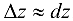 , то, используя представление
, то, используя представление 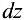 по формуле (15.1), получим
по формуле (15.1), получим
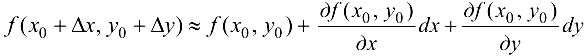
приближенная формула, верная с точностью до бесконечно малых более высоких порядков относительно 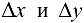 .
.
Пример 15.1.
Вычислить приближенно 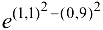 .
.
Решение:
Рассмотрим функцию 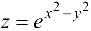 . Искомое число можно считать приращенным значением функции в точке
. Искомое число можно считать приращенным значением функции в точке 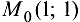 при
при 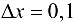 ,
, 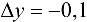 .
.
Согласно формуле (15.2): 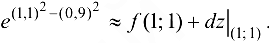 .
.
Поскольку 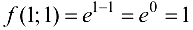 ,
,
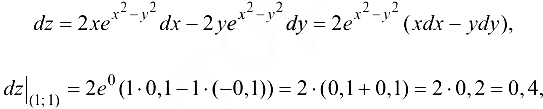
то окончательно получим 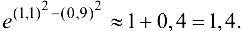 .
.
Ответ: 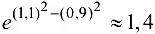 .
.
С помощью полного дифференциала функции можно также выяснить, как отражаются на значении функции погрешности ее аргументов.
Пример 15.2.
Определить предельную абсолютную погрешность 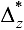 функции
функции 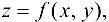 , зная предельные абсолютные погрешности
, зная предельные абсолютные погрешности 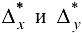 . ее аргументов
. ее аргументов 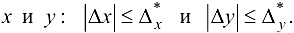
Решение:
По определению: 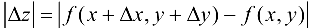 .
.
Заменяя приращение функции ее дифференциалом, получим
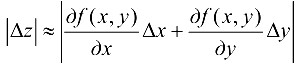
откуда можно получить оценку:
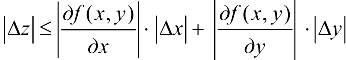
Следовательно, за предельную абсолютную погрешность функции 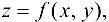 можно принять
можно принять
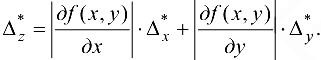
Используя (15.3), можно также определить относительную погрешность функции 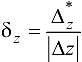 .
.
Ответ: 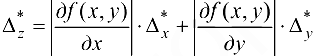
Определение 15.2. Полным дифференциалом второго порядка функции 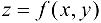 называется полный дифференциал от ее полного дифференциала.
называется полный дифференциал от ее полного дифференциала.
По определению, получим
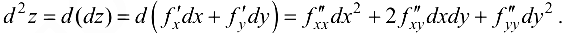
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

