Пример задачи 7.1
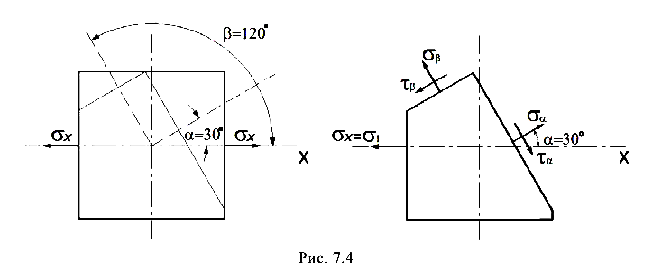
На элементарный параллелепипед, выделенный в окрестности некоторой точки деформированного стержня, действует нормальное напряжение 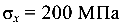 (рис. 7.4).
(рис. 7.4).
Определить значения нормальных и касательных напряжений по площадкам под углом 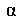 = 30° и
= 30° и 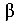 = 120° к исходной грани, а также значение наибольшего касательного напряжения.
= 120° к исходной грани, а также значение наибольшего касательного напряжения.
Решение
Элементарный параллелепипед находится в условиях линейного напряженного состояния, так как по его граням действуют только нормальные напряжения и только в одном направлении. Исходя из этого, 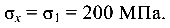
По площадкам параллелепипеда под углом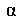 = 30° и
= 30° и 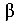 = 120° действуют нормальные и касательные напряжения (см. рис. 7.4), которые определяются по формулам (7.1), (7.2):
= 120° действуют нормальные и касательные напряжения (см. рис. 7.4), которые определяются по формулам (7.1), (7.2):
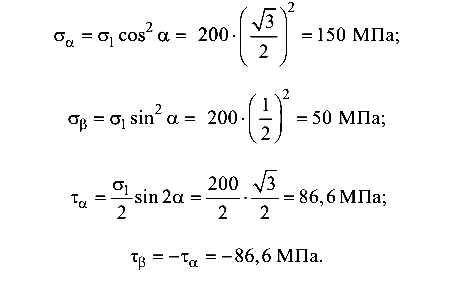
Наибольшее касательное напряжение будет действовать в сечении под углом 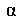 = 45° к оси Х:
= 45° к оси Х:
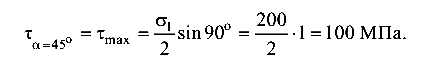
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
