Переменная величина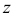 
называется функцией двух переменных величин 
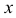и 
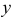, если каждой паре допустимых значени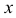й и 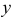соответствует единственное значение 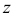(записывают так: 
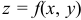). Существует понятие многозначной функции (самостоятельно изучите). Функцию двух переменных можно назвать как функцию точки 
.
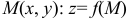Переменная величина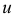 
называется функцией трех переменных величин 
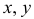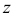и , если каждой тройке допустимых значени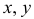й и 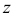соответствует единственное значение 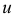(записывают так: 
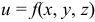). Функцию трех переменных можно назвать как функцию точки 
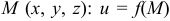. Аналогично определяется функция 
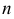переменных 
: 
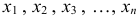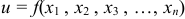. Совокупность значений 
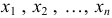называют точкой 
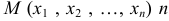— мерного пространства, а функцию 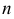переменных — функцией точки 
.
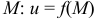Техника и естествознание дают много примеров функций нескольких переменных. Например, формула Клайперона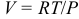 
, где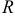 
— некоторая постоянная, 
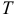— абсолютная температура, 
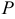— давление , 
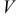— объем данной массы газа, позволяет рассматривать объем как функцию двух переменных 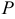и 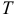. Объем прямоугольного параллелепипеда (
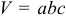) является функцией трех переменных 
.
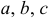Основные сведения будем излагать для функций двух и трех переменных. Многие понятия и формулы для этих функций легко распространяются по аналогии на случай 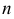переменных (читайте предлагаемую литературу).
Множество всех точек, в которых определена функция нескольких переменных, называется областью определения функции (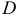
). Для функции двух переменных область определения 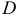— некоторая часть плоскости или вся плоскость (
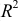). Для функции трех переменных область определения 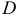— некоторая часть пространства или все пространство (
).
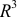Геометрическим изображением функции двух переменных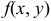 
называется некоторая поверхность в пространстве, проектирующая на плоскость 
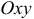в область 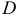. Функции трех переменных не имеют геометрического представления.
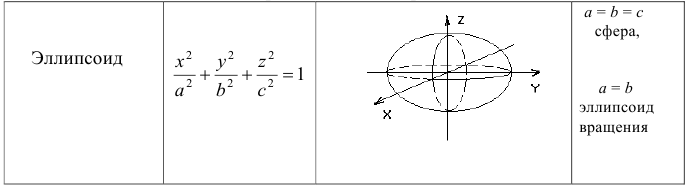
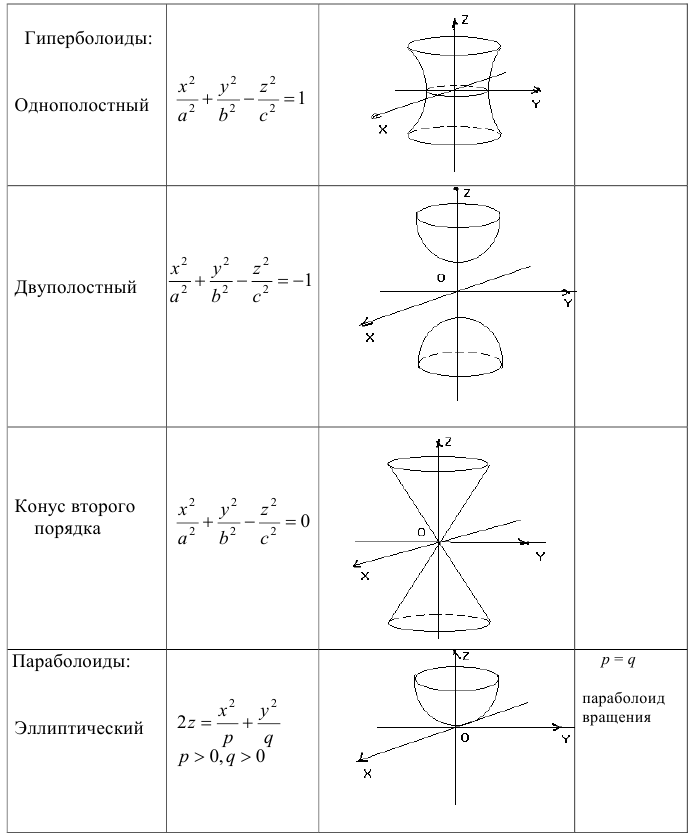
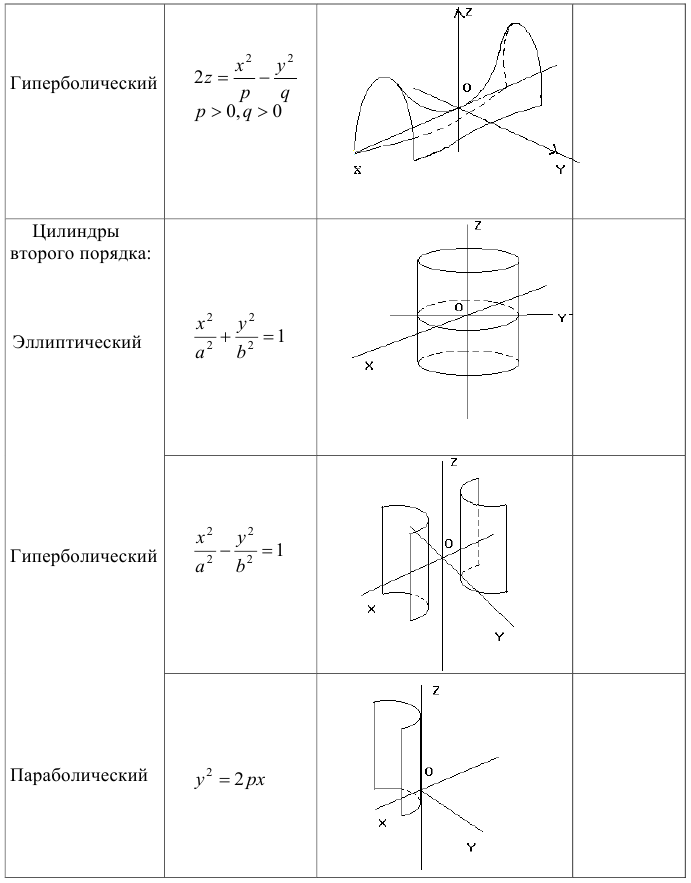
Поверхности 2 — го порядка
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
