Оглавление:
Пусть дана однородная система
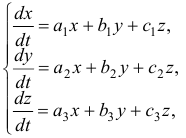
где 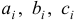 — постоянные. Будем искать частные решения системы в виде
— постоянные. Будем искать частные решения системы в виде 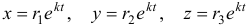 , где
, где 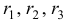 и
и 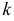 — неопределенные коэффициенты, которые следует найти. Уравнение
— неопределенные коэффициенты, которые следует найти. Уравнение
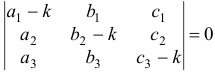
называется характеристическим уравнением системы. Отыскав корни этого уравнения, и поочередно подставляя их в исходную систему, определим коэффициенты 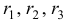 .
.
Пример №1
Найти общее решение системы
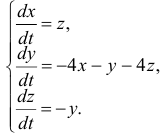
Решение:
Система в данном случае имеет вид: 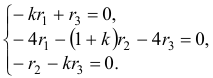
Характеристическое уравнение 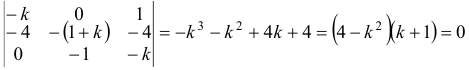 имеет корни
имеет корни 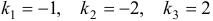 . Для
. Для 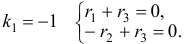 Решением этой системы будут, например, числа
Решением этой системы будут, например, числа 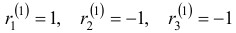 (здесь
(здесь 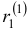 выбрано произвольно). Следовательно,
выбрано произвольно). Следовательно, 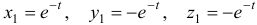 . Для
. Для 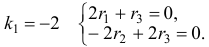 Решая эту систему, получим
Решая эту систему, получим 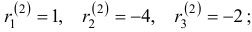 тогда
тогда 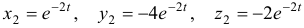 .
.
Наконец, для 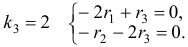 Здесь можно положить
Здесь можно положить 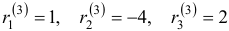 и будем иметь
и будем иметь 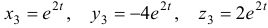 .
.
Общее решение данной системы дифференциальных уравнений таково:
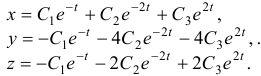
Пример №2
Решить систему
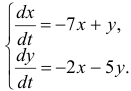
Решение:
Чаще системы дифференциальных уравнений записывают в виде: 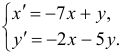 Составим характеристическое уравнение
Составим характеристическое уравнение 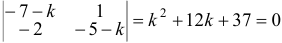 и найдем его корни
и найдем его корни 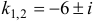 . Так как эти корни комплексные, система уравнений будет иметь комплексные коэффициенты и даст комплексные значения для чисел
. Так как эти корни комплексные, система уравнений будет иметь комплексные коэффициенты и даст комплексные значения для чисел 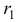 и
и 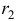 . В этом случае, учитывая возможность произвольного выбора
. В этом случае, учитывая возможность произвольного выбора 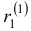 и
и 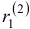 , целесообразно сразу положить
, целесообразно сразу положить 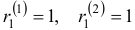 и, записав функцию
и, записав функцию 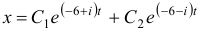 или, что то же самое,
или, что то же самое, 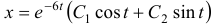 , найти функцию
, найти функцию 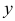 , используя первое уравнение системы:
, используя первое уравнение системы: 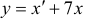 . Для этого найдем
. Для этого найдем 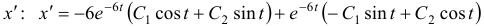 или
или 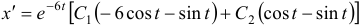 . Подставляя
. Подставляя 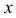 и
и 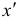 в первое уравнение системы, получим
в первое уравнение системы, получим 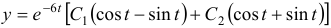 . Общим решением системы будет
. Общим решением системы будет 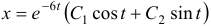 и
и 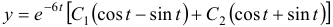 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Метод вариации произвольных постоянных |
| Сведение системы к одному дифференциальному уравнению высшего порядка |
| Задачи, приводящие к дифференциальным уравнениям с примером решения |
| Числовые поля |

