Уравнением Бернулли называется уравнение вида 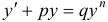 (здесь
(здесь 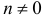 и
и 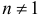 ).
).
Это уравнение приводится к линейному с помощью подстановки 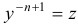 . Решим линейное уравнение относительно функции
. Решим линейное уравнение относительно функции 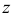 и подставим вместо
и подставим вместо 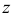 выражение
выражение 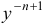 . Получим общий интеграл уравнения Бернулли.
. Получим общий интеграл уравнения Бернулли.
Пример:
Найти общее решение уравнения 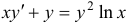 .
.
Решение:
Разделив обе части уравнения на 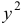 , получим:
, получим: 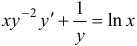 . Введем новую переменную
. Введем новую переменную 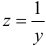 , тогда
, тогда 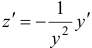 . Подставляя в уравнение, получим:
. Подставляя в уравнение, получим: 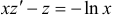 . Это линейное уравнение относительно функции
. Это линейное уравнение относительно функции 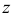 . Применим метод вариации произвольной постоянной:
. Применим метод вариации произвольной постоянной:
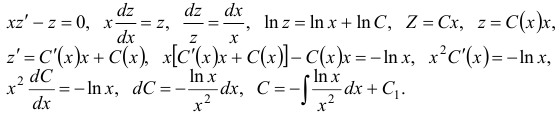
Интегрируя по частям, находим 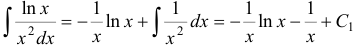 , следовательно,
, следовательно,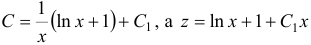 . Заменяя теперь
. Заменяя теперь 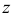 на
на 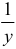 , получим:
, получим: 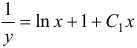 или
или 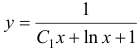 . Это и есть общее решение исходного уравнения.
. Это и есть общее решение исходного уравнения.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Однородные уравнения первого порядка |
| Линейные уравнения первого порядка |
| Уравнения вида y(n) = f(x) |
| Уравнения не содержащие: (y) |

