Теорема 1. Если два вектора 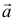 и
и 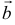 определены своими декартовыми прямоугольными координатами
определены своими декартовыми прямоугольными координатами 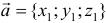 ,
, 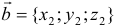 , то
, то
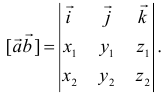
Следствие. Если два вектора 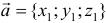 и
и 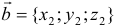 коллинеарны, то координаты их пропорциональны, т.е.
коллинеарны, то координаты их пропорциональны, т.е. 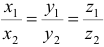 .
.
Иногда в знаменателях могут стоять нули. Чтобы избежать этого, мы будем понимать пропорции 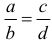 в смысле
в смысле 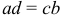 .
.
Теорема 2. Если три вектора 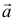 ,
, 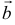 и
и 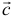 определены декартовыми прямоугольными координатами
определены декартовыми прямоугольными координатами 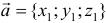 ,
, 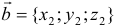 и
и 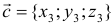 , то смешанное произведение
, то смешанное произведение 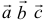 равняется определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е.
равняется определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е.
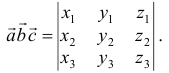
Следствие. Необходимым и достаточным условием компланарности трех векторов 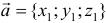 ,
, 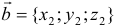 и
и 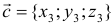 является равенство нулю определителя
является равенство нулю определителя
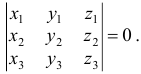
Если вектор 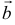 векторно умножается на вектор
векторно умножается на вектор 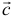 , а вектор
, а вектор 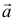 также векторно умножается на векторное произведение
также векторно умножается на векторное произведение 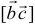 , то получившийся при этом вектор
, то получившийся при этом вектор 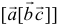 называется двойным векторным произведением.
называется двойным векторным произведением.
Теорема. Для любых векторов 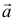 ,
, 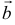 и
и 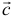 справедлива формула
справедлива формула
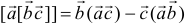 или
или 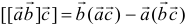 .
.
Для запоминания этой формулы удобно правило: двойное векторное произведение равно среднему вектору, умноженному на скалярное произведение двух остальных, минус другой вектор внутреннего произведения, умноженный на скалярное произведение двух остальных.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Векторное произведение векторов |
| Смешанное произведение трех векторов |
| Алгебраические линии и поверхности |
| Различные виды уравнения прямой на плоскости |
