Оглавление:
Определителем (детерминантом) второго порядка называется число
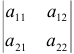, определяемое равенством 
.
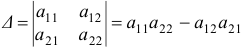Числа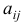 
(
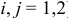) называются элементами определителя. Первый индекс 
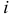указывает номер строки, второй 
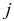— номер столбца. Строки и столбцы называют рядами определителя. Порядок определителя равен количеству его строк или столбцов.
Для вычисления определителя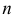 
-го порядка сформулируем теорему:
Определитель 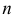-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения т. е.
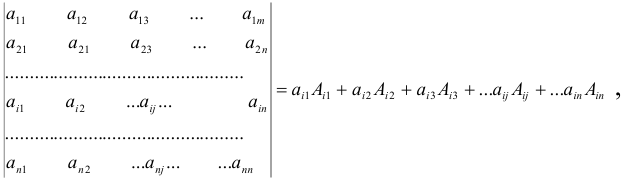
где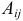 
— алгебраическое дополнение элемента 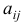. В частности,
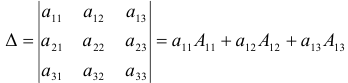
Алгебраическим дополнением 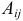элемента 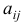называется минор 
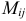, взятый со знаком «+», если сумма индексов — четное число и со знаком «-», если сумма индексов 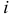и 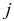— нечетное число, т.е 
.
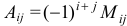Минором 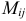элемента 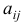определителя 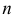-го порядка называется определитель 
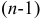-го порядка, получающийся из данного определителя в результате вычеркивания 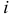-ой строки и 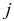-го столбца.
Пример 1.
Вычислить определитель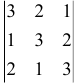 
.
Решение:
Разложим определитель по элементам первой строки, используя теорему
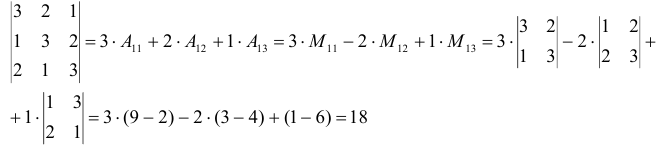
Ответ: 18
Если определитель третьего порядка разложить по первой строке, то получим формулу:
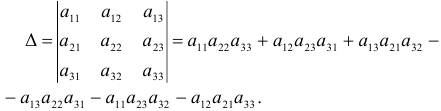
Элементы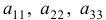 
образуют главную диагональ определителя, а элементы 
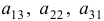— побочную диагональ определителя. Чтобы запомнить эту формулу, прибегают к графическому ее изображению.
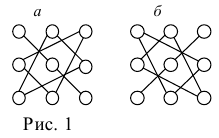
Такой метод вычисления определителя третьего порядка получил название правило «треугольников». При вычислении определителя со знаком «+» берутся произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников с основаниями, параллельными этой диагонали (рис. 1а); со знаком «-» берутся произведения элементов, стоящих на побочной диагонали и в вершинах двух треугольников с основаниями, параллельными этой диагонали (рис. 16).
Пример 2.
Вычислить определитель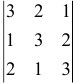 
Решение:
По правилу «треугольников»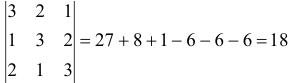 
.
Другой способ вычисления определителя третьего порядка — по правилу Саррюса. Для этого к определителю третьего порядка приписываются справа два первых столбца. Складывают произведения элементов со знаком «+» на диагоналях, параллельных главной, и со знаком «-» на диагоналях, параллельных побочной, т.е.
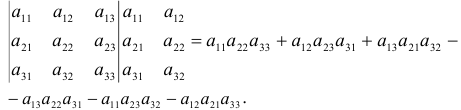
Пример 3.
Вычислить определитель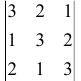 
Решение:
По правилу Саррюса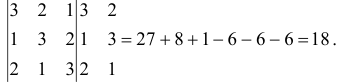 
Основные свойства определителей
- Величина определителя не изменится при замене всех его строк соответствующими столбцами.
- Величина определителя меняет знак на противоположный при перестановке двух соседних параллельных рядов.
- Общий множитель элементов какого-либо ряда определителя можно выносить за знак определителя.
- Определитель с двумя одинаковыми параллельными рядами равен нулю.
- Величина определителя не изменится, если к элементам какого-либо ряда прибавить соответственно элементы другого параллельного ряда, умноженные на произвольное число.
Пример 4.
Вычислить определитель:
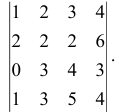
Решение:
Определитель четвертого порядка вычисляется разложением по элементам какого-либо ряда. Обычно выбирают ряд, у которого часть элементов равна нулю. Если нулевых элементов нет, то, используя 5-е свойство определителя, получают три нуля в каком-либо ряде.
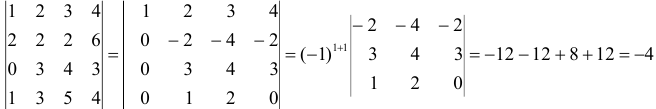
Из второй строки вычли первую, предварительно умноженную на два; из четвертой строки вычли первую; разложили определитель по элементам первого столбца.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Векторный анализ: основные понятия и пример с решением |
| Ряды в высшей математике |
| Матрицы. Операции над матрицами |
| Системы линейных уравнений |
