Оглавление:
Задание: Переход от алгебраической формы к тригонометрической и показательной и обратно.
Цель: формирование умения выполнять переход между различными формами комплексных чисел.
Задание для самостоятельной внеаудиторной работы:
54.1. Разберите технику перехода от тригонометрической, показательной и алгебраической форм ко всем остальным.
54.2. Закончите высказывания:
а) Алгебраическая форма комплексного числа имеет вид: 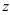 = …, где … — действительная часть, … -мнимая часть комплексного числа.
= …, где … — действительная часть, … -мнимая часть комплексного числа.
б) Тригонометрическая форма комплексного числа имеет вид: 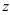 = …, где
= …, где 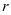 — …,
— …, 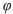 — ….
— ….
в) Показательная форма комплексного числа имеет вид: 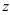 = …, где
= …, где 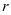 — …,
— …, 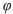 — ….
— ….
г) Алгоритм перехода от алгебраической формы к тригонометрической и показательной включает следующие 4 этапа: …
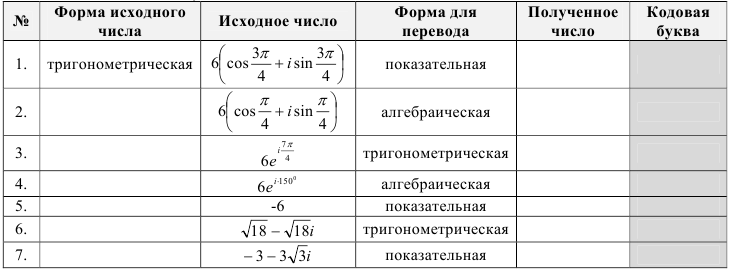
54.3. Заполните таблицу:
Мы уже знаем, что каждому комплексному числу соответствует точка на плоскости. Возведем число в квадрат — появляется другая точка, еще раз возведем в квадрат (или любую другую степень), появляется новая точка на плоскости. Потом эту простейшую операцию повторим многократно с получающимся каждый раз новым комплексным числом. В зависимости от начального числа могут быть несколько вариантов. Однако при некоторых начальных значениях новые числа группируются внутри какой-либо области, а при отображении их на плоскости появляются невероятные изображения. Это группирование возводимых в квадрат комплексных чисел впервые подметил и описал Жюлиа в 1916 году. Как называются эти удивительно красивые изображения. Вы узнаете, выполнив задание 54.3.

Мы видим геометрическую фигуру, в которой один и тог же мотив повторяется в последовательно уменьшающемся масштабе. Про такие фигуры говорят, что они моделируют сами себя. Такая геометрия тесно связана с теорией хаоса. В природе существует много примеров: от раковины и цветной капусты до гор и листьев. Эта теория нашла широчайшее применение в компьютерной графике.
Карта ответов:


Если Вас заинтересовала данная великолепная математическая теория, Вы можете посмотреть интересные видео в сети Интернет, перейдя по ссылкам:
- http://www.youtube.com/watch?v=b3adw5igSzI;
- http://www.voutube.com/watch?v=CfyOCXpR9Lo&feature=related;
- http://www.youtube.com/watch?v=fr05uRumlNA&feature=relmfu;
- http://www.youtube.com/watch?v=Yke32Oavr 11&feature=related.
54.4. Выполните задания для подготовки к практической работе:
а) решите уравнение: 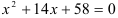 ;
;
б) вычислите: 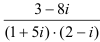 ;
;
в) вычислите: 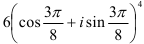 ;
;
г) представьте число в тригонометрической и показательной формах: 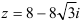 ;
;
д) представьте число в показательной форме: 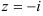 . Найдите все
. Найдите все 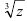 и постройте их на комплексной плоскости.
и постройте их на комплексной плоскости.
54.5. Найдите модуль и аргумент комплексного числа: 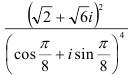 .
.
Методические указания по выполнению работы:
Итак, существуют три формы записи комплексного числа:
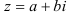 — алгебраическая форма (1);
— алгебраическая форма (1);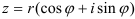 — тригонометрическая форма (2);
— тригонометрическая форма (2);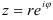 — показательная форма (3).
— показательная форма (3).
Переход от тригонометрической и показательной формы
Для того чтобы осуществить переход от тригонометрической формы комплексного числа к показательной и наоборот, достаточно выделить в записи числа значение модуля 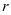 и аргумента
и аргумента 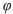 и подставить их в другую форму.
и подставить их в другую форму.
Для того чтобы осуществить переход от тригонометрической формы комплексного числа к алгебраической, необходимо вычислить значения 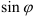 и
и 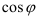 по таблицам значений тригонометрических функций.
по таблицам значений тригонометрических функций.
Пример 1.
Переведите комплексное число 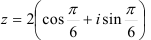 в показательную и алгебраическую формы.
в показательную и алгебраическую формы.
Решение:
Выделим в записи числа значение модуля 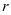 и аргумента
и аргумента 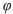 :
: 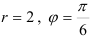 . Подставим их в формулу (3):
. Подставим их в формулу (3): 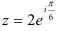 — показательная форма.
— показательная форма.
Для записи заданного комплексного числа в алгебраической форме вычислим 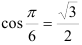 и
и 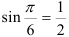 и подставим их в тригонометрическую форму:
и подставим их в тригонометрическую форму:
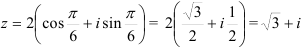 — алгебраическая форма.
— алгебраическая форма.
Ответ: 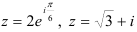 .
.
Пример 2.
Переведите комплексное число 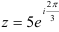 в тригонометрическую и алгебраическую формы.
в тригонометрическую и алгебраическую формы.
Решение:
Выделим в записи числа значение модуля 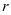 и аргумента
и аргумента 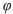 :
: 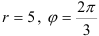 . Подставим их в формулу (2):
. Подставим их в формулу (2): 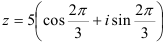 — тригонометрическая форма.
— тригонометрическая форма.
Для записи заданного комплексного числа в алгебраической форме вычислим с использованием формул приведения 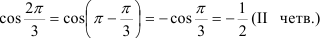 и
и 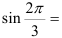
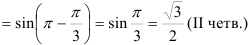 и подставим их в тригонометрическую форму:
и подставим их в тригонометрическую форму:
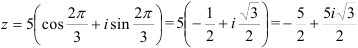 — алгебраическая форма.
— алгебраическая форма.
Ответ: 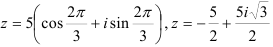 .
.
Переход от алгебраической формы к тригонометрической и показательной.
Для того чтобы осуществить переход от алгебраической формы к тригонометрической и показательной, будем использовать следующий алгоритм:
1. Выделите параметры 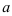 и
и 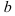 в алгебраической форме
в алгебраической форме 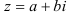 .
.
2. Найдите модуль комплексного числа 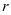 по формуле:
по формуле: 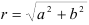 .
.
3. Для нахождения аргумента 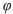 выполните вспомогательный чертеж и определите четверть, в которой расположен вектор
выполните вспомогательный чертеж и определите четверть, в которой расположен вектор 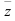 (а, следовательно, и угол
(а, следовательно, и угол 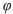 ).
).
4. В зависимости от четверти, в которой лежит угол 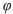 , воспользуйтесь одной из следующих формул:
, воспользуйтесь одной из следующих формул:
- если
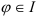 четверти, то
четверти, то 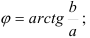
- если
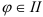 четверти, то
четверти, то 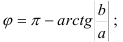
- если
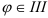 четверти, то
четверти, то 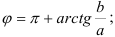
- если
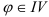 четверти, то
четверти, то 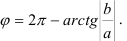
5. Подставьте найденные значения 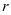 и
и 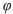 в тригонометрическую и показательную формы.
в тригонометрическую и показательную формы.
Пример 3.
Переведите комплексное число 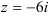 в показательную и тригонометрическую формы.
в показательную и тригонометрическую формы.
Решение:
1. Выделим параметры 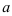 и
и 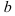 в алгебраической форме
в алгебраической форме
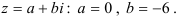
2. Найдем модуль комплексного числа 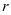 по формуле
по формуле 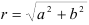 :
:
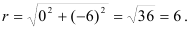
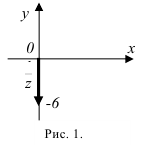
3. Для нахождения аргумента 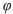 выполним вспомогательный чертеж (рис. 1). Видим, что полученный вектор образует с положительным направлением оси
выполним вспомогательный чертеж (рис. 1). Видим, что полученный вектор образует с положительным направлением оси  угол
угол 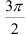 , следовательно, без применения дополнительных формул делаем вывод, что
, следовательно, без применения дополнительных формул делаем вывод, что 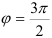 .
.
4. Так как 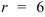 , а
, а 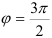 , то тригонометрическая форма комплексного числа имеет вид:
, то тригонометрическая форма комплексного числа имеет вид: 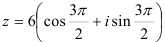 . Показательная форма того же числа равна
. Показательная форма того же числа равна 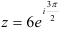 .
.
Ответ: 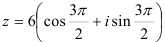 ,
, 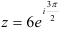 .
.
Пример 4.
Переведите комплексное число 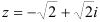 в показательную и тригонометрическую формы.
в показательную и тригонометрическую формы.
Решение:
1. Выделим параметры 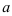 и
и 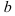 в алгебраической форме
в алгебраической форме 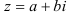 :
:

2. Найдем модуль комплексного числа 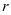 по формуле
по формуле 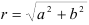 :
:
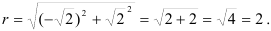
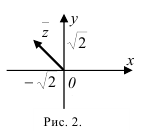
3. Для нахождения аргумента 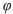 выполним вспомогательный чертеж (рис. 2). Видим, что полученный вектор (а, следовательно, и угол
выполним вспомогательный чертеж (рис. 2). Видим, что полученный вектор (а, следовательно, и угол 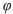 ) расположен во второй четверти.
) расположен во второй четверти.
4. Воспользуемся формулой: если 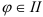 четверти, то
четверти, то 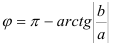 .
.
Тогда 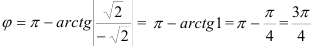 .
.
5. Так как 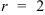 , а
, а 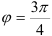 , то тригонометрическая форма комплексного
, то тригонометрическая форма комплексного
числа имеет вид: 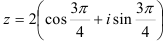 . Показательная форма того же числа равна
. Показательная форма того же числа равна 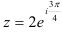 .
.
Ответ: 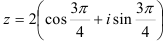 ,
, 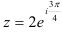 .
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

