Оглавление:
Задание:. Приложения двойных интегралов в геометрии.
Цель: формирование умения применять двойные интегралы для вычисления объёмов цилиндрических тел и площадей плоских геометрических фигур.
Задание для самостоятельной внеаудиторной работы:
37.1. Выучите определение цилиндрического тела. Выясните, как используется двойной интеграл для вычисления его объёма. Внимательно изучите пример вычисления объёма цилиндрического тела с помощью двойного интеграла.
37.2. Вычислите объём цилиндрического тела, ограниченного сверху поверхностью 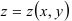 , а снизу — прямоугольной областью
, а снизу — прямоугольной областью 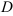 :
:
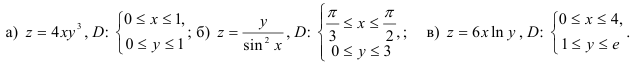
37.3. Вычислите объём цилиндрического тела, ограниченного сверху поверхностью 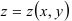 , а снизу — областью
, а снизу — областью 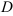 :
:
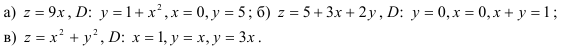
37.4. Выясните, как используется двойной интеграл для вычисления площади плоской геометрической фигуры. Внимательно изучите пример нахождения площади плоской фигуры с помощью двойного интеграла.
37.5. Вспомните, как вычисляется площадь плоской фигуры с помощью определённого интеграла. Проведите сравнительный анализ техник двойного и определённого интегрирования для вычисления площадей плоских фигур.
37.6. Вычислите площадь плоской геометрической фигуры, ограниченной линиями:
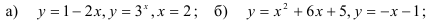
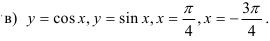
Методические указания по выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
Двойной интеграл используется для вычисления объёма цилиндрического тела и нахождения площади плоской геометрической фигуры.
Рассмотрим функцию 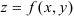 , непрерывную и неотрицательную в некоторой замкнутой области
, непрерывную и неотрицательную в некоторой замкнутой области  плоскости
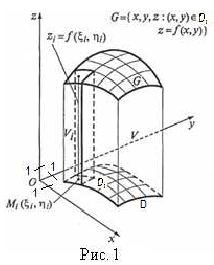
плоскости 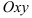 . Тело, ограниченное сверху поверхностью
. Тело, ограниченное сверху поверхностью 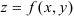 , снизу — замкнутой областью
, снизу — замкнутой областью 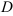 , с боков — цилиндрической поверхностью, образующая которой параллельна оси
, с боков — цилиндрической поверхностью, образующая которой параллельна оси 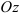 , а направляющей служит граница области
, а направляющей служит граница области 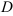 , называется цилиндрическим (цилиндроидом) (рис. 1).
, называется цилиндрическим (цилиндроидом) (рис. 1).
Геометрический смысл двойного интеграла заключается в том, что величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела: 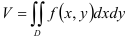 .
.
Рассмотрим пример вычисления объёма цилиндрического тела с помощью двойного интеграла.
Пример 1.
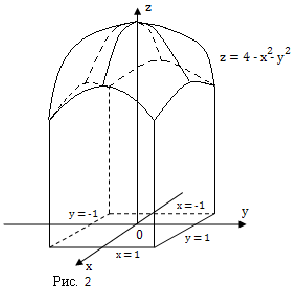
Найдите объём цилиндрического тела, изображённого на рисунке (рис.2), ограниченного сверху поверхностью 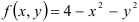 , снизу — плоскостью
, снизу — плоскостью 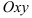 , с боков плоскостями
, с боков плоскостями 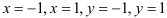 .
.
Решение:
Поскольку геометрически двойной интеграл от неотрицательной функции равен объёму цилиндрического тела, будем использовать формулу: 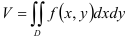 .
.
В нашем случае 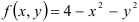 . Область интегрирования
. Область интегрирования 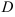 , что хорошо видно на рисунке, представляет собой фигуру на плоскости
, что хорошо видно на рисунке, представляет собой фигуру на плоскости 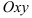 , ограниченную прямыми
, ограниченную прямыми 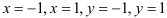 , т.е. является прямоугольной областью. Следовательно, для нахождения объёма данного цилиндрического тела надо вычислить двойной интеграл по прямоугольной области, т.е.
, т.е. является прямоугольной областью. Следовательно, для нахождения объёма данного цилиндрического тела надо вычислить двойной интеграл по прямоугольной области, т.е.
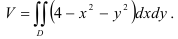
Будем использовать соответствующую формулу сведения двойного интеграла к повторному:
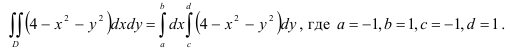
Таким образом, 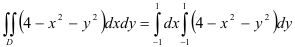 .
.
Вычислим полученный повторный интеграл:
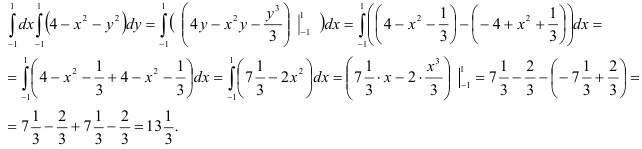
В итоге 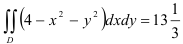 . Следовательно,
. Следовательно, 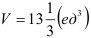 .
.
Ответ: 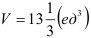 .
.
Пример 2.
Найдите объем цилиндрического тела, ограниченного сверху поверхностью 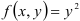 , снизу — областью
, снизу — областью 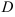 плоскости
плоскости 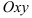 , представляющей собой прямоугольный треугольник, образованный координатными осями и прямой
, представляющей собой прямоугольный треугольник, образованный координатными осями и прямой 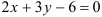 .
.
Решение:
В силу геометрического смысла двойного интеграла от неотрицательной функции, для нахождения объёма цилиндрического тела будем использовать формулу:
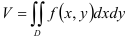
Вычислим двойной интеграл 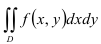 по области
по области 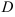 . Для этого построим область интегрирования
. Для этого построим область интегрирования 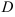 в прямоугольной декартовой системе координат на плоскости. Составим уравнение прямой
в прямоугольной декартовой системе координат на плоскости. Составим уравнение прямой 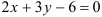 с угловым коэффициентом:
с угловым коэффициентом: 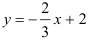 . Построим эту прямую по двум точкам:
. Построим эту прямую по двум точкам:
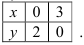
Изображенная на рисунке область интегрирования  (рис.З) является криволинейной областью. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
(рис.З) является криволинейной областью. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
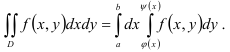
В нашем случае 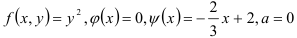 .
.
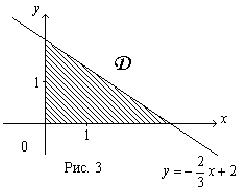
Найдем 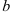 как абсциссу точки пересечения прямой
как абсциссу точки пересечения прямой 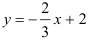 с осью
с осью 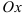 , решив уравнение:
, решив уравнение: 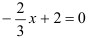 .
.
Получим 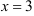 , значит
, значит 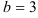 . Следовательно,
. Следовательно,
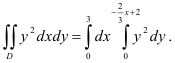
Вычислим полученный повторный интеграл:
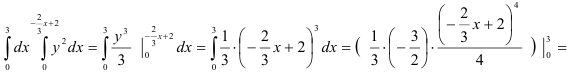
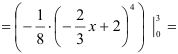
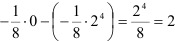 . В итоге,
. В итоге, 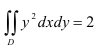 . Следовательно,
. Следовательно, 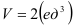 .
.
Ответ: 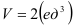 .
.
Рассмотрим в качестве 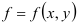 в формуле
в формуле 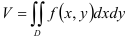 единичную функцию
единичную функцию 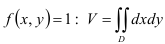 . Тогда цилиндрическое тело «превратится» в прямой цилиндр с высотой, равной 1, и основанием —
. Тогда цилиндрическое тело «превратится» в прямой цилиндр с высотой, равной 1, и основанием — 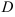 . Объём такого цилиндра
. Объём такого цилиндра 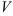 численно совпадает с площадью
численно совпадает с площадью 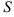 его основания
его основания 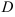 . Таким образом, площадь плоской фигуры
. Таким образом, площадь плоской фигуры 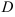 можно находить но формуле:
можно находить но формуле:
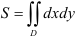
Геометрический смысл двойного интеграла от единичной функции заключается в том, что величина двойного интеграла от единичной функции по области 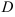 равна площади плоской фигуры, представляющей собой область интегрирования
равна площади плоской фигуры, представляющей собой область интегрирования 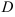 .
.
Рассмотрим пример вычисления площади плоской фигуры с помощью двойного интеграла.
Пример 3.
Найдите площадь плоской фигуры, ограниченной линиями 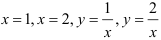 .
.
Решение:
Поскольку геометрически двойной интеграл от единичной функции по области 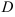 равен площади плоской фигуры, представляющей собой область интегрирования
равен площади плоской фигуры, представляющей собой область интегрирования 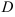 , будем использовать формулу:
, будем использовать формулу: 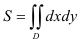 .
.
В нашем случае областью интегрирования 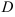 является фигура, ограниченная линиями
является фигура, ограниченная линиями 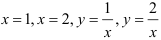 . Вычислим
. Вычислим 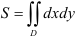 .
.
Для этого построим область интегрирования 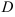 в прямоугольной декартовой системе координат на плоскости.
в прямоугольной декартовой системе координат на плоскости.
Линии, задаваемые уравнениями 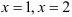 , — прямые, параллельные оси
, — прямые, параллельные оси 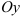 и проходящие соответственно через точки (1 ;0), (2;0). Линия, задаваемая уравнением
и проходящие соответственно через точки (1 ;0), (2;0). Линия, задаваемая уравнением 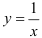 — гипербола, «ветви» которой расположены в I и III координатных четвертях. Гиперболу
— гипербола, «ветви» которой расположены в I и III координатных четвертях. Гиперболу 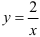 можно получить из гиперболы
можно получить из гиперболы 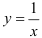 с помощью растяжения последней вдоль оси ординат в два раза.
с помощью растяжения последней вдоль оси ординат в два раза.
Описание линий, задающих область интегрирования 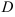 , позволяет при ее построении ограничиться I координатной четвертью.
, позволяет при ее построении ограничиться I координатной четвертью.
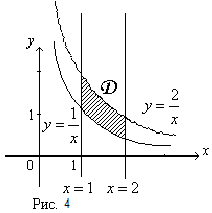
Изображенная на рисунке область интегрирования 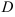 (рис.4) является криволинейной областью. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
(рис.4) является криволинейной областью. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
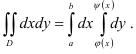
В нашем случае 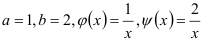 . Следовательно,
. Следовательно, 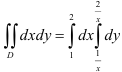 .
.
Вычислим полученный повторный интеграл:
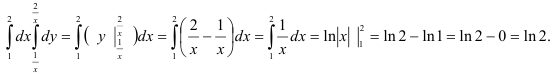
В итоге, 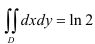 . Следовательно,
. Следовательно, 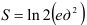 .
.
Ответ: 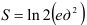 .
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

