Оглавление:
Задание 36. Нахождение двойных интегралов но прямоугольной области и произвольной области 1 типа -2 ч.
Целы формирование умения вычислять двойные интегралы по прямоугольной и криволинейной областям.
Задание для самостоятельной внеаудиторной работы:
36.1. Выясните, какая область интегрирования является прямоугольной. Запишите и запомните формулы сведения двойного интеграла к повторному по данной области. Внимательно изучите пример вычисления двойного интеграла по прямоугольной области.
36.2. Вычислите двойной интеграл от функции 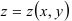 по прямоугольной области
по прямоугольной области 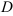 :
:
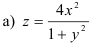 , область
, область 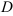 ограничена линиями:
ограничена линиями: 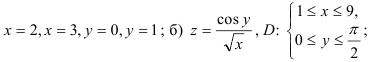
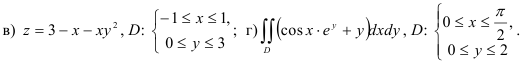
36.3. Выясните, какая область интегрирования является криволинейной. Запишите и запомните формулу сведения двойного интеграла к повторному по данной области. Внимательно изучите пример вычисления двойного интеграла по криволинейной области.
36.4. Вычислите двойной интеграл от функции 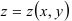 по криволинейной области
по криволинейной области 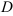 , ограниченной линиями:
, ограниченной линиями:
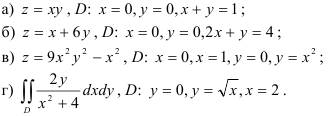
36.5. Вычислите двойной интеграл по произвольной области 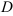 :
:
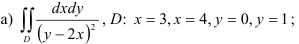
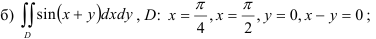
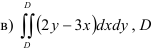 ограничена
ограничена 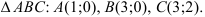
Методические указания no выполнению работы:
Для успешного решения задач необходимо знание следующего теоретического материала:
Двойным интегралом от функции 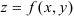 по области
по области 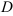 называется предел последовательности интегральных сумм, не зависящий ни от способа разбиения области
называется предел последовательности интегральных сумм, не зависящий ни от способа разбиения области 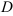 на элементарные области, ни от выбора точек в них, при условии, что число слагаемых каждой интегральной суммы неограниченно возрастает, а наибольший из диаметров разбиения стремится к нулю:
на элементарные области, ни от выбора точек в них, при условии, что число слагаемых каждой интегральной суммы неограниченно возрастает, а наибольший из диаметров разбиения стремится к нулю: 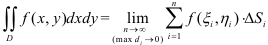 .
.
Двойной интеграл вычисляется путем сведения его к повторному с применением соответствующей формулы. Вид формулы, по которой осуществляется сведение, зависит от типа области интегрирования. Различают два типа области интегрирования: прямоугольную и криволинейную. Поэтому при вычислении двойного интеграла возникают две ситуации.
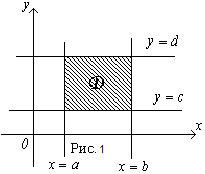
1. Область интегрирования 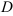 на плоскости
на плоскости 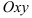 является прямоугольной, т.е. ограничена прямыми
является прямоугольной, т.е. ограничена прямыми 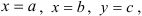
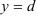 , причем
, причем 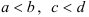 (рис.1). В этом случае формула сведения двойного интеграла к повторному имеет вид:
(рис.1). В этом случае формула сведения двойного интеграла к повторному имеет вид:
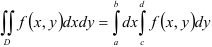 или
или
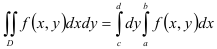
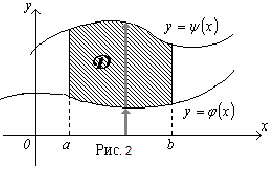
2. Область интегрирования 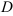 на плоскости
на плоскости 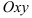 является криволинейной областью, т.е. ограничена снизу и сверху непрерывными кривыми
является криволинейной областью, т.е. ограничена снизу и сверху непрерывными кривыми 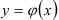 и
и 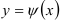 , а слева и справа — отрезками прямых
, а слева и справа — отрезками прямых 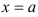 и
и 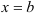 так, что любая прямая, параллельная оси
так, что любая прямая, параллельная оси 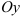 и проходящая внутри отрезка
и проходящая внутри отрезка 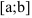 пересекает границу области (кривые
пересекает границу области (кривые 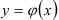 и
и 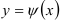 ) в двух точках (рис.2).
) в двух точках (рис.2).
В этом случае формула сведения двойного интеграла к повторному имеет вид:
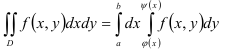
При вычислении двойных интегралов удобно использовать следующий алгоритм:
- Построить область интегрирования в прямоугольной декартовой системе координат на плоскости (исключением может быть случай прямоугольной области).
- Определить тип области и в соответствии с ним составить формулу сведения двойного интеграла к повторному.
- Вычислить полученный повторный интеграл.
Рассмотрим примеры вычисления двойных интегралов.
Пример 1.
Вычислите двойной интеграл 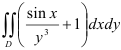 по прямоугольной области
по прямоугольной области 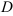 , ограниченной прямыми
, ограниченной прямыми 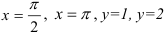 .
.
Решение:
Воспользуемся алгоритмом вычисления двойного интеграла. Поскольку область интегрирования является прямоугольной, мы не будем изображать её в прямоугольной декартовой системе координат на плоскости.
1. Для вычисления двойного интеграла но прямоугольной области используем соответствующую формулу сведения его к повторному интегралу:
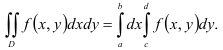
В нашем случае 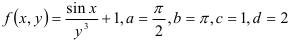 . Следовательно,
. Следовательно, 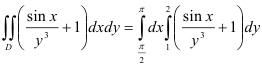 .
.
2. Вычислим полученный повторный интеграл:
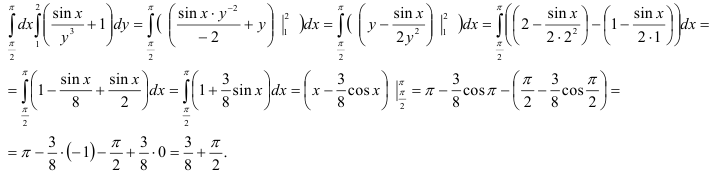
Таким образом, окончательно имеем:
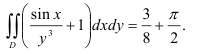
Этот двойной интеграл по прямоугольной области можно вычислить также с использованием формулы
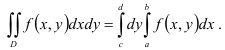
Тогда 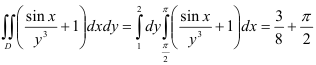 .
.
Ответ: 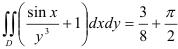 .
.
Пример 2.
Вычислите двойной интеграл 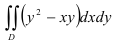 по области
по области 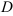 , ограниченной линиями
, ограниченной линиями 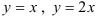 и
и 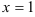 .
.
Решение:
Воспользуемся алгоритмом вычисления двойного интеграла.
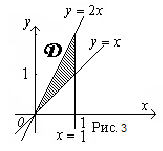
1) Построим область интегрирования 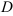 в прямоугольной декартовой системе координат на плоскости (рис.З) . Линия, задаваемая уравнением
в прямоугольной декартовой системе координат на плоскости (рис.З) . Линия, задаваемая уравнением 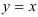 , — прямая, являющаяся биссектрисой I и III координатных углов.
, — прямая, являющаяся биссектрисой I и III координатных углов.
Линия, задаваемая уравнением 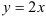 , — прямая. Построим ее по двум точкам:
, — прямая. Построим ее по двум точкам:
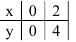
Линия, задаваемая уравнением 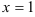 , — прямая, параллельная оси
, — прямая, параллельная оси 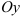 и проходящая через точку (1;0).
и проходящая через точку (1;0).
В итоге, область интегрирования 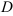 обозначена на рис. 29.5. штриховкой.
обозначена на рис. 29.5. штриховкой.
2) Область интегрирования 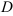 является криволинейной областью. Для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
является криволинейной областью. Для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
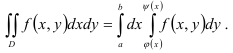
В нашем случае 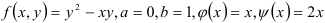 . Следовательно,
. Следовательно,
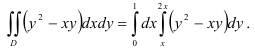
3) Вычислим полученный повторный интеграл:
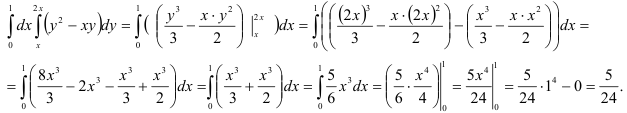
Таким образом, окончательно имеем:
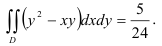
Ответ: 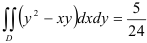 .
.
На этой странице вы сможете посмотреть все остальные темы готовых контрольных работ по высшей математике:
Готовые контрольные работы по высшей математике
Обратите внимание на похожие контрольные работы возможно они вам будут полезны:

