Оглавление:
Пусть задана функция 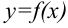 , непрерывная на промежутке
, непрерывная на промежутке 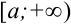 . Если существует конечный предел
. Если существует конечный предел 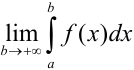 , то его называют несобственным интегралом первого рода и обозначают
, то его называют несобственным интегралом первого рода и обозначают 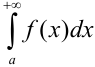 .
.
Таким образом, по определению 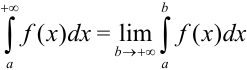 .
.
Если найденный предел равен конечному числу, то говорят, что несобственный интеграл 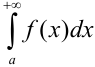 сходится. Если указанный предел не существует или бесконечен, то говорят, что интеграл
сходится. Если указанный предел не существует или бесконечен, то говорят, что интеграл 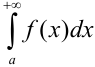 расходится.
расходится.
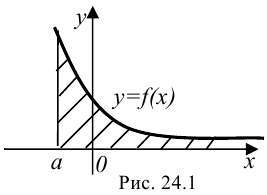
Геометрический смысл несобственного интеграла I рода заключается в следующем: если 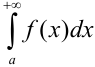 сходится (при условии, что
сходится (при условии, что 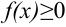 ), то он представляет собой площадь «бесконечно длинной» криволинейной трапеции (рис. 24.1).
), то он представляет собой площадь «бесконечно длинной» криволинейной трапеции (рис. 24.1).
Аналогично вводится понятие несобственного интеграла с бесконечным нижним пределом интегрирования для непрерывной на промежутке 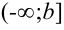 функции:
функции: 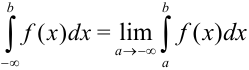 .
.
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется формулой: 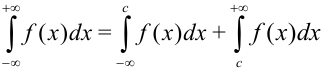 , где
, где 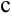 — произвольное число.
— произвольное число.
Рассмотрим примеры нахождения несобственных интегралов I рода.
Пример №24.1.
Вычислите несобственный интеграл или установите его расходимость: 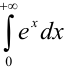 .
.
Решение:
Для нахождения несобственного интеграла с бесконечной верхней границей от непрерывной функции воспользуемся формулой: 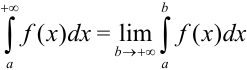 . Тогда
. Тогда 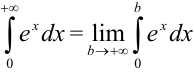 . Сначала вычислим интеграл от
. Сначала вычислим интеграл от 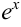 :
: 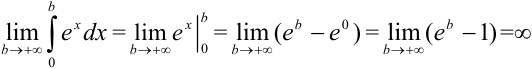 . Получили, что несобственный интеграл расходится.
. Получили, что несобственный интеграл расходится.
Ответ: 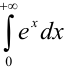 расходится.
расходится.
Пример №24.2.
Вычислите несобственный интеграл или установите его расходимость: 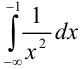 .
.
Решение:
Подынтегральная функция 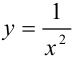 непрерывна на промежутке
непрерывна на промежутке 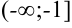 . Для нахождения несобственного интеграла I рода с бесконечной нижней границей воспользуемся формулой:
. Для нахождения несобственного интеграла I рода с бесконечной нижней границей воспользуемся формулой: 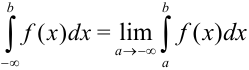 . Тогда
. Тогда 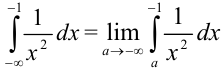 . Вычислим интеграл, содержащийся под знаком предела:
. Вычислим интеграл, содержащийся под знаком предела: 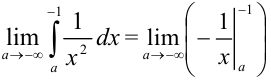 . Избавимся от знака «минус», поменяв границы интегрирования местами:
. Избавимся от знака «минус», поменяв границы интегрирования местами: 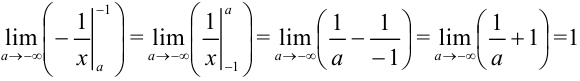 . Получили, что рассматриваемый несобственный интеграл сходится.
. Получили, что рассматриваемый несобственный интеграл сходится.
Ответ: 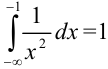 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Вычисление длины дуги плоской кривой и объема тел вращения. |
| Понятие несобственного интеграла |
| Несобственные интегралы II рода. |
| Задачи, приводящие к понятию функции нескольких переменных. |

