Оглавление:



Плоскости, касательные к поверхностям
- Самолет в контакте с IIOIIEPYIIOCTJIH 1. Проведите произвольные кривые a, b, c, … через нормальные точки M на кривой поверхности Q (рис. 180) и постройте касательные t \ t / 3 к этим кривым в точке M , Все касательные Плоскость называется касательной к поверхности.
- Следовательно, касательная плоскость — это геометрическая траектория всех касательных, нарисованных на определенной кривой поверхности, которая проходит через одну из точек. Очевидно, что для построения касательной плоскости на поверхности в точке M достаточно нарисовать только две кривые a и b на этой поверхности и построить касательные 0 и / 2 на них.
Эти две касательные определяют касательную плоскость. Людмила Фирмаль
Конечно, вам нужно выбрать простейшую линию в виде такой кривой на поверхности. Таким образом, для линейчатой поверхности одна из этих кривых действует как прямая образующая (соответствует касательной) и является параллельной для вращающейся поверхности.
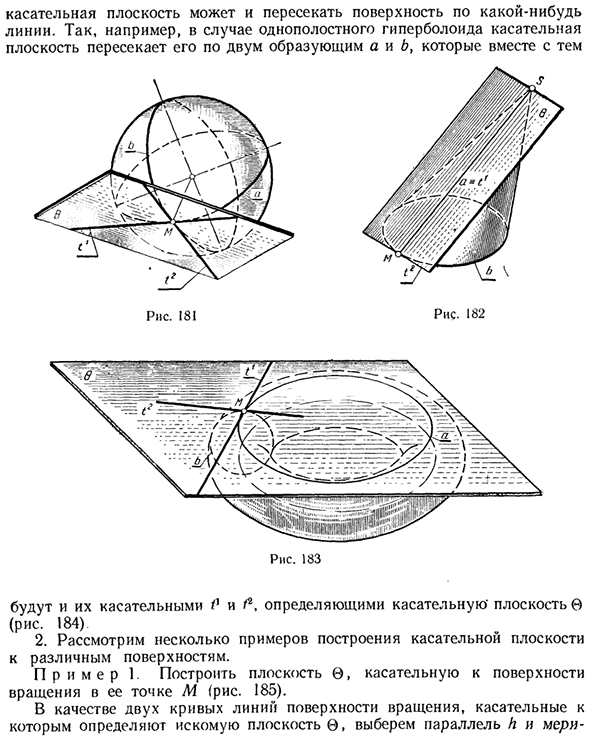
В зависимости от типа поверхности касательная плоскость является общей с поверхностью, например, в случае сферы (рис. 181) или в случае конической поверхности (рис. 182) или поверхности с бесчисленными общими точками, которые образуют прямую линию или кривую. Вы можете иметь только одно кольцо (рис. 183).
В приведенном выше случае поверхность находится на одной стороне касательной плоскости и не пересекает поверхность. но 1 Эта позиция была доказана в процессе дифференциальной геометрии. Итак, тангенциальная плоскость или Не ясно или уникально. Примером такой точки является пик Коническая поверхность. Касательная плоскость может пересекать поверхность на любой прямой.
- Так, например, для одного гиперболоида касательная плоскость пересекается вдоль двух генераторов a и b. Рис. 181 Рис. 183 Касательные линии 0 и f2. Определить касательную плоскость с помощью (рис. 184) 2. Рассмотрим некоторые примеры построения касательных плоскостей к различным поверхностям. Пример 1. Создайте плоскость, которая касается вращающейся поверхности в точке M (Рисунок 185).
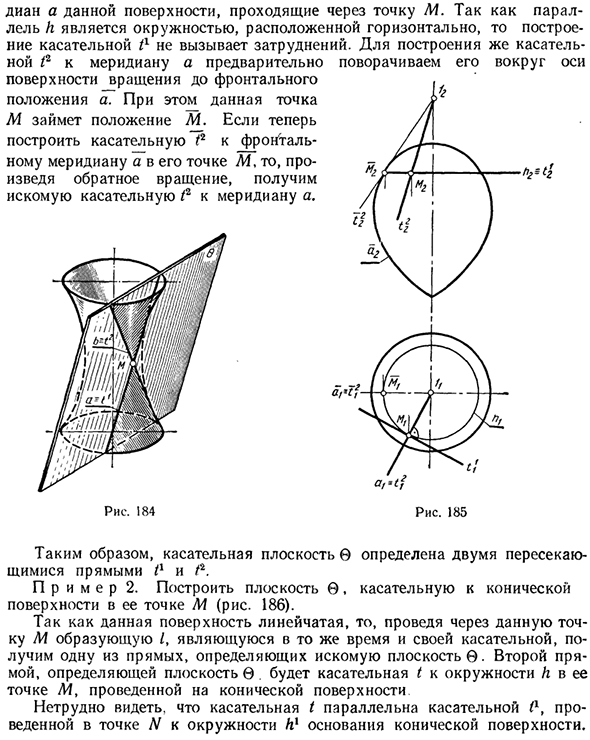
Выберите параллель h и измерьте в качестве двух кривых плоскости вращения тангенс, который определяет желаемую плоскость. Рис. 182 Диана заданной поверхности, проходящая через точку М. Поскольку параллель h является горизонтальной окружностью, нетрудно построить касательную tl.
Чтобы создать тангенс / 2 меридиана a, сначала поверните меридиан вокруг оси вращения. Людмила Фирмаль
Правило а. Кроме того, эта точка М занимает положение М. Создать касательную Т2 впереди Для основного меридиана А в этой точке М ^ /], Реверсирование вращения дает T «** 2 Желательная касательная к меридиану / 2. / Я г Рисунок \ B5 Следовательно, касательная плоскость определяется двумя пересекающимися линиями 0 и / 2. Пример 2. Создайте плоскость, которая касается конической поверхности в точке M (рис. 186).
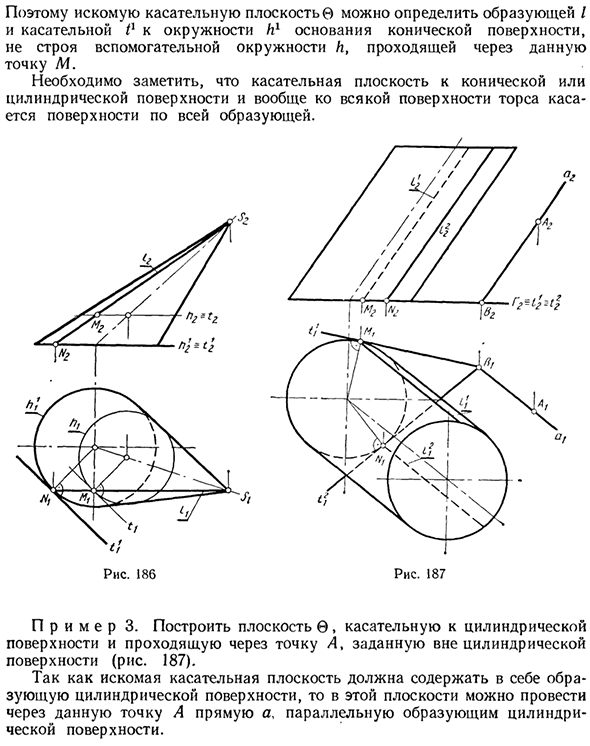
Поскольку эта поверхность проходит через указанную точку М и одновременно проходит через ее касательный генератор /, она получает одну из линий, определяющих интересующую плоскость. Вторая линия, определяющая плоскость 0, является касательной к окружности h в этой точке и нарисована на конической поверхности.
Легко видеть, что касательная t параллельна касательной il, нарисованной в точке N окружности hx на дне конической поверхности. Рис. 184 Таким образом, желаемую касательную плоскость можно определить по касательной к окружности 11 на нижней поверхности генератора / конической поверхности без построения вспомогательной окружности здания через конкретную точку М.
Обратите внимание, что коническая или цилиндрическая поверхность и, как правило, касательная к любой поверхности фюзеляжа, контактирует с поверхностью по всей образующей. Пример 3. Создайте плоскость, которая касается цилиндрической грани и проходит через точку А, определенную вне цилиндрической грани (Рисунок 187).
Поскольку целевая касательная плоскость должна содержать образующую цилиндрической поверхности, эта плоскость может рисовать прямую линию a, которая проходит через заданную точку A параллельно образующей цилиндрической поверхности. Если мы проходим через точку B-пересечение прямой a и плоскости.
Γ-касательных к окружности дна цилиндрической поверхности / 1 и / 2, линии a и касательные tl и / 3 являются двумя желаемыми касательными плоскостями b1 (ax / *) И определите B2 (Oh / 2). Эти плоскости контактируют с цилиндрической поверхностью вдоль ее генераторов Ix и / 2. Помимо определения касательной плоскости выше, она может быть указана в других условиях, но ее природа зависит от типа поверхности.
Таким образом, вы можете нарисовать касательную плоскость на сфере и установить следующие условия: Прошел определенную линию, которая не пересекает сферу. Был параллельно конкретной плоскости. такие как Касательная плоскость может быть нарисована в конус, который выглядит так: Пройдите через точку вне поверхности конуса. Это было параллельно прямой линии. такие как
Смотрите также:
Решение задач по начертательной геометрии

