Поверхности вращения

Оглавление:

Поверхности вращения

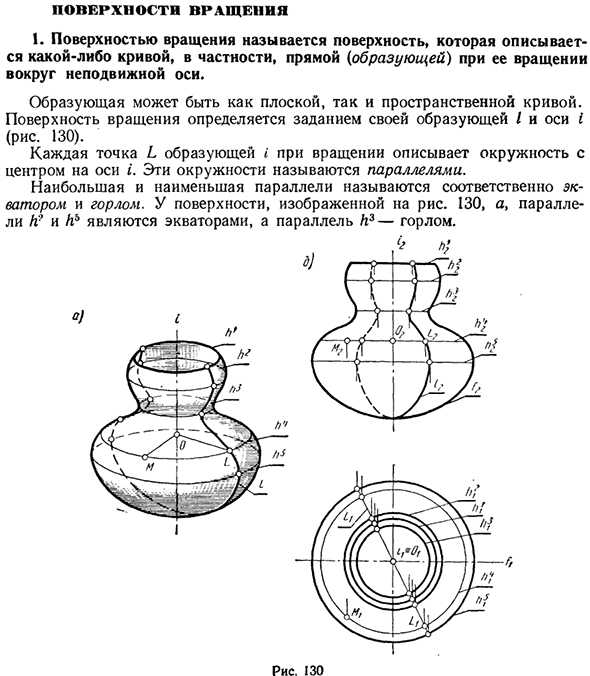
Поворотная поверхность 1. Поворотная поверхность — это поверхность, представленная произвольной кривой, особенно прямой линией (шиной) при вращении вокруг фиксированной оси. Генераторы могут быть как плоскими, так и пространственными кривыми. Плоскость вращения определяется настройкой ее шины / и оси I (рис. 130).

Каждая точка L вращающегося генератора i представляет круг с центром на оси i. На поверхности, показанной на схеме под позицией 130a, параллельные линии H} и hb представляют собой экватор, а параллельная линия L3 представляет собой горло. 6 А. » Рис. 130 Плоскость вращения изогнутой плоскости, проходящей через ось I, называется меридианом.

Эти круги называются параллелями. Максимальные и минимальные параллели называются экватором и горлом соответственно. Людмила Фирмаль

Легко видеть, что все меридианы равны друг другу. При рисовании вращающейся поверхности на сложном чертеже поверхность обычно располагается так, чтобы ось i была перпендикулярна плоскости проекции. Рисунок 130, b-ось tJLPi. Затем все параллельные линии проецируются на плоскость Ilj без искажений, а экватор hb и горловина L3 определяют горизонтальный контур поверхности.

Меридиан на фронтальной плоскости проецируется без искажения на плоскость А2. Этот меридиан называется основным меридианом и определяет фронтальный профиль поверхности. Чтобы выбрать точку M на плоскости вращения, выберите ее фронтальную проекцию M2. Затем вы можете легко построить горизонтальную проекцию Mi из точки M, используя параллель L4, нарисованную на уровне M.

130 точек М должны быть видны в передней проекции. Поворотные поверхности наиболее широко используются в различных механизмах и деталях машин. Основной причиной этого является, с одной стороны, широкое использование вращательного движения, а с другой стороны, простота обработки вращающейся поверхности.

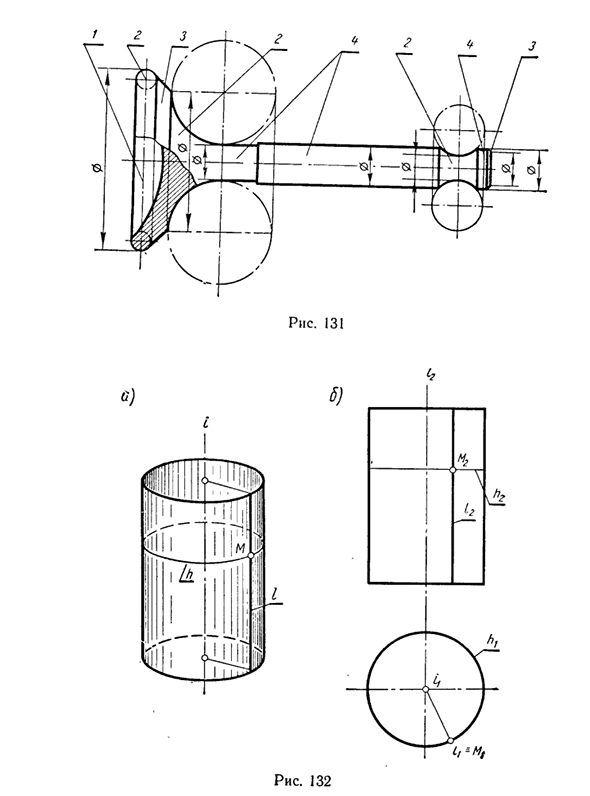
На фиг.131 показан клапан двигателя, ограниченный различными видами вращающихся поверхностей, то есть сферическими поверхностями 7. Торус 2 \ Конус 3 \ Цилиндр 4. 2. Рассмотрим поверхность, образованную вращением прямой линии. Вращающийся цилиндр образован вращением вокруг оси i, параллельной линии / (рис. 132).

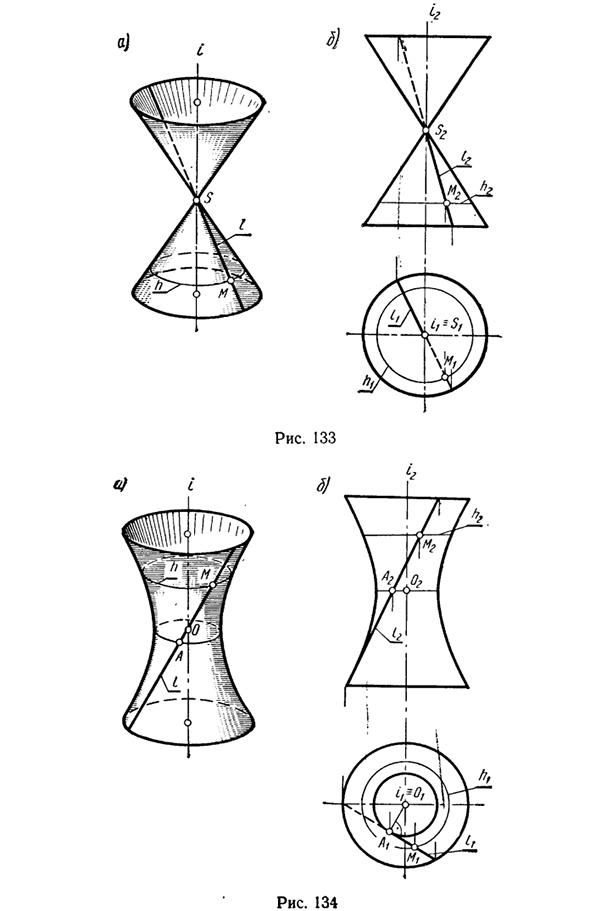
Вращающийся конус образуется вращением вокруг прямой / пересекающейся оси i (рис. 133). Однополостной вращающийся гиперболоид образован вращением линии I вокруг оси i, пересекающей его (рис. 134). Когда линия / вращается вокруг оси i, все точки линии рисуют окружности с разными радиусами, и общий вертикальный AO линий I и i является наименьшим из всех радиусов, поэтому точка A является гиперболоидом.

Представляет круг, который является шеей. Чтобы создать гиперболический главный меридиан, достаточно повернуть точку линии I вокруг оси i, пока она не присоединится к фронту, проходящему через ось i. Далее получите гиперболу. Рассматриваемая вращающаяся поверхность может быть отнесена к классу линейчатых поверхностей, поскольку она образована движением прямой линии.

Гипербола — это фронтальный набросок одного гиперболоида. Людмила Фирмаль

Кроме того, эти поверхности являются вторичными поверхностями. Максимальное количество пересечений между каждой из этих поверхностей и прямой линией равно двум. Построение точки M на любой из вращающихся поверхностей, описанных выше (см. Рис. 132-134), может быть выполнено с использованием параллельного генератора h или прямой линии i.

При использовании зубчатых колес или фрикционных колес для передачи вращения используются все три из этих вращающихся поверхностей. Так вперед Рисунок 135 Вращение по параллельной оси выполняется с использованием цилиндрического колеса (рис. 135, а), конического зубчатого колеса с поперечной осью (рис. 135. б) и гиперболоидного колеса с поперечной осью (рис. 135, в). ) 3.

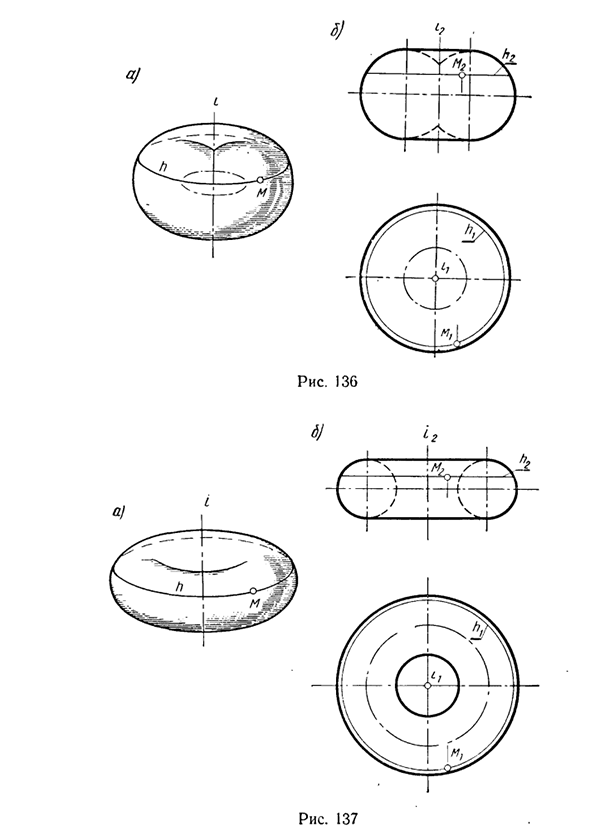
Рассмотрим поверхность, образованную вращением круга. Сфера образована вращением круга вокруг диаметра i. Тор образуется при вращении круга вокруг оси круга в плоскости, но не проходит через центр (рис. 136). Кроме того, если ось i проходит вне круга, то тор называется кольцом (рис. 137). •

Сфера — это квадратичная поверхность, а тор — это четверть, соответствующая максимальному числу пересечений этих поверхностей с прямой линией. Построение как сферы, так и точки тора M выполняется с использованием параллельной h. 4. Рассмотрим поверхность, образованную вращением квадратичной кривой — эллипса, параболы, гиперболы вокруг их осей.

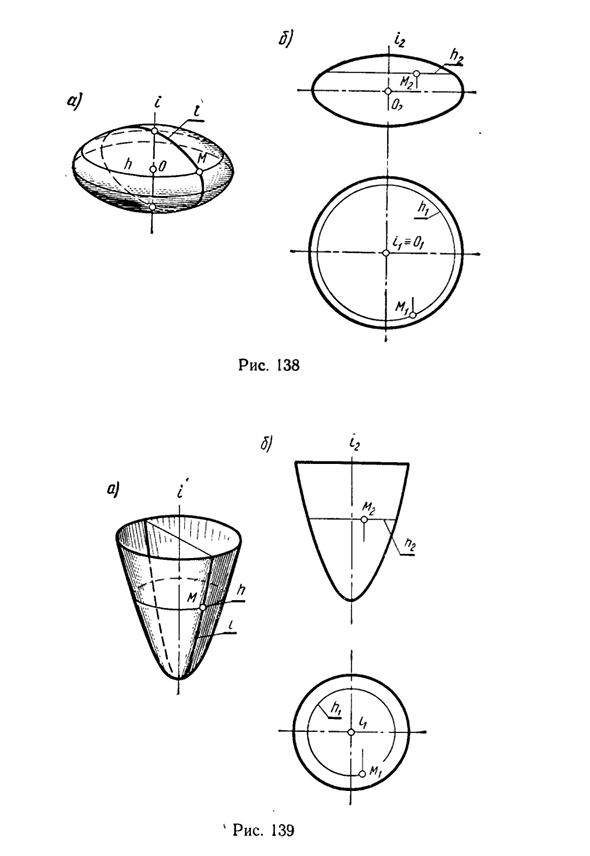
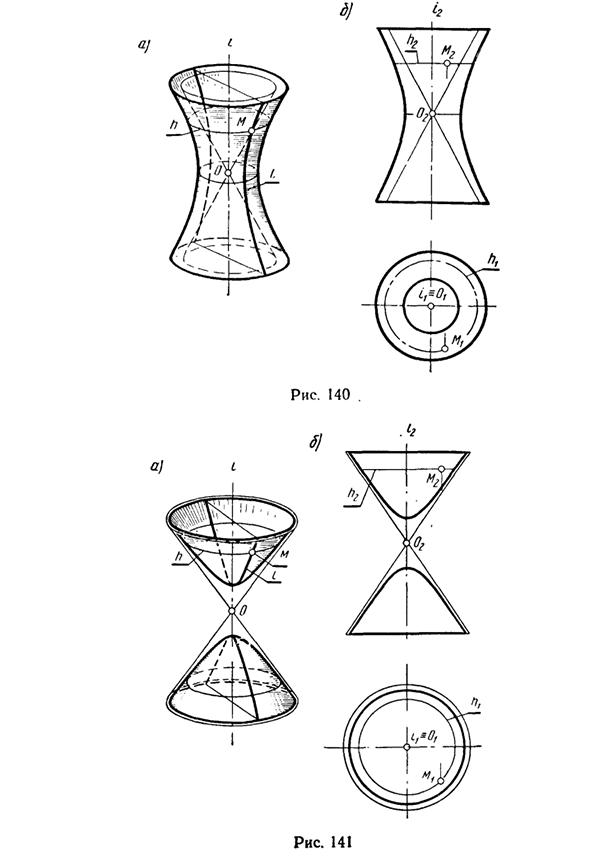
Сфероид образуется вращением эллипса вокруг своей оси i (рис. 138). Параболоид образуется при вращении параболы вокруг оси i (рис. 139). (Параболоид вращения используется в качестве отражающей поверхности прожектора и создает параллельные лучи.) Вращающийся гиперболоид с одной полостью формируется вращением гиперболы вокруг ее мнимой оси i (рис. 140).

Как показано, однополостной вращающийся гиперболоид является доминирующей поверхностью и может быть сформирован путем вращения прямой линии вокруг своей пересекающейся оси (см. Рис. 134). На рисунке 140, помимо гиперболоида, асимптотическим вращающимся конусом, образованным вращением гиперболической асимптоты, образующей гиперболу Пок, является азан. Внешняя часть этого конуса имеет однослойный гиперболоид.

Вращающийся гиперболоид с двумя полостями формируется вращением гиперболы вокруг ее реальной оси i (рис. 141). Когда эта гиперболическая асимптота вращается, во внутренней области, где расположены гиперболоиды двух листов, получается асимптотический вращающийся конус. Вышеуказанные четыре поверхности являются вторичными поверхностями. Построение точек M на каждой из этих поверхностей выполняется с использованием их параллельных линий h (см. Рис. 138-141).

Плоскости, касательные к поверхностям	Линейчатые поверхности
Общие сведения о способах построения линий взаимного пересечения двух поверхностей	Поверхности второго порядка