Оглавление:
В курсе высшей математики рассматриваются несколько пределов, получивших название «замечательные». Приведем некоторые из них:
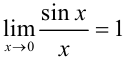— первый замечательный предел;
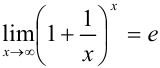— второй замечательный предел, аналогичный тому, что был рассмотрен нами в лекции 8, где 
принадлежало множеству натуральных чисел.
Пользуясь этими формулами, можно вычислить ряд пределов.
Пример №9.9.
Вычислите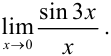 
Решение:
Поскольку под знаком синуса стоит угол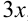 
, домножим числитель и знаменатель дроби на 3, чтобы выражение под знаком синуса и выражение в знаменателе стали равны: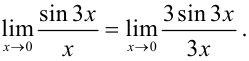 
Вынесем число 3 за знак предела (следствие 1):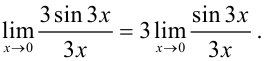 
Применив первый замечательный предел, получим, что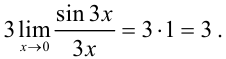 
Ответ: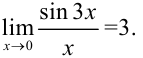 
Пример №9.10.
Вычислите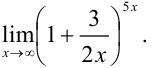 
Решение:
Постараемся преобразовать выражение под знаком предела таким образом, чтобы прийти ко второму замечательному пределу. Необходимо, чтобы числитель дроби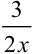 
был равен 1. Для этого разделим числитель и знаменатель данной дроби на 3; получим дробь вида: 
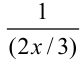. Теперь постараемся преобразовать показатель степени 
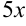таким образом, чтобы в нем можно было выделить множитель 
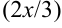. Для этого 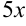домножаем на 2 и 3 и делим на 2 и 3:
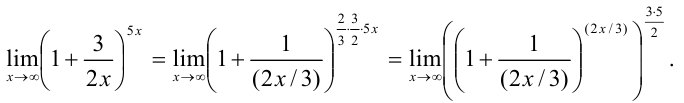
Применив к выражению в скобках второй замечательный предел, получим, что
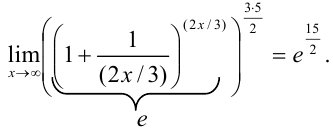
Ответ: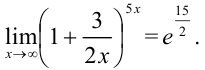 
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Техника вычисления пределов. |
| Предел функции на бесконечности. |
| Непрерывность функции в точке и на промежутке. |
| Основные теоремы о непрерывных функциях. |
